1. Định nghĩa
Một đường thẳng gọi là vuông góc với mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng ấy.
Định lí 1:
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì đường thẳng d vuông góc với mặt phẳng (P).
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba.
2. Tính chất
Tính chất 1.
Có duy nhất một mặt phẳng (P) đi qua một điểm O cho trước và vuông góc với một đường thẳng a cho trước.
Mặt phẳng vuông góc với AB tại trung điểm O của đoạn AB, gọi là mặt phẳng trung trực của đoạn thẳng AB (h.3.26).
3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
Tính chất 3.
a) Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng song song với nhau.
Tính chất 5.
a) Cho đường thẳng a và mặt phẳng (P) song song với nhau. Đường thẳng nào vuông góc với (P) thì cũng vuông góc với a.
b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
4. Phép chiếu vuông góc
Định nghĩa:
Phép chiếu song song lên mặt phẳng (P) theo phương l vuông góc với mặt phẳng (P) gọi là phép chiếu vuông góc lên mặt phẳng (P).
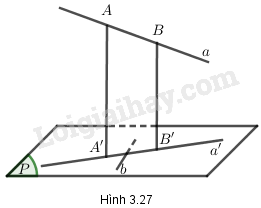
Định lí ba đường vuông góc:
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). khi đó điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a' của a trên (P) (h.3.27).
5. Góc giữa đường thẳng và mặt phẳng
Định nghĩa:
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa a và (P) bằng \(90^{0} .\)
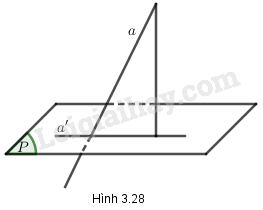
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a' của nó trên (P), gọi là góc giữa đường thẳng a và mặt phẳng (P) (h.3.28).
Chú ý: góc giữa đường thẳng và mặt phẳng không vượt quá \(90^{0} .\)
soanvan.me