1. Định nghĩa
Cho điểm \(O\) và góc lượng giác \(α\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M'\) sao cho \(OM' = OM\) và góc lượng giác \(( OM; OM')\) bằng \(α\) được gọi là phép quay tâm \(O\) góc \(α\).
Điểm \(O\) được gọi là tâm quay còn \(α\) được gọi là góc quay của phép quay đó.
Phép quay tâm \(O\) góc \(α\) thường được ký hiệu \(Q_{\left ( O,\alpha \right )}\).
2. Nhận xét
a) Chiều dương của phép quay trùng với chiều dương của đường tròn lượng giác, đó là chiều ngược với chiều quay của kim đồng hồ.
b) Đặc biệt:
- Phép quay \({Q_{(O, 2k \pi )}}\) với mọi số nguyên \(k\) là phép đồng nhất.
- Phép quay \({Q_{(O, (2k+1)\pi)}}\) với mọi số nguyên \(k\) là phép đối xứng tâm \(O\)
3. Tính chất
+) Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.
+) Phép quay biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính.
+) Phép quay góc \(α\) với \(0 ≤ |α| ≤\) \(\frac{\pi }{2}\), biến đường thẳng \(d\) thành đường thằng \(d'\) sao cho góc giữa \(d\) và \(d'\) bằng \(|α|\).
Ví dụ:
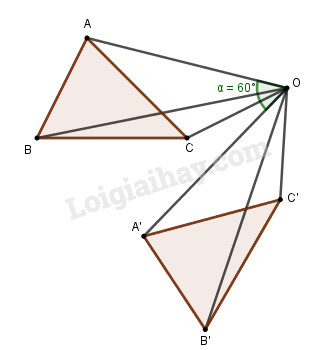
Cho tam giác \(ABC\) và điểm \(O\) nằm ngoài tam giác. Dựng ảnh của tam giác qua phép quay tâm \(O\) góc quay \({60^0}\).
soanvan.me
