Câu hỏi mục 1
Video hướng dẫn giải
a) Nhiệt lượng toả ra ở dây dẫn khi có dòng điện chạy qua phụ thuộc vào những yếu tố: cường độ dòng điện, điện trở của dây dẫn, thời gian dòng điện chạy qua, và sự phụ thuộc đó được biểu thị bằng hệ thức: \(Q = I^2.R.t\)
b) Hệ thức biểu thị mối liên hệ giữa Q và các địa lượng \(m_1, m_2\), \(c_1, c_2\), \(t_1^0,t_2^0\) là:
\(Q = (c_1.m_1 + c_2.m_2).(t_1^0 - t_2^0)\)
c) Nếu toàn bộ nhiệt lượng tỏa ra bởi dây dẫn điện trở R có dòng điện cường độ I chạy qua trong thời gian t được dùng để đun nóng nước và cốc trên đây thì độ tăng nhiệt độ Δto = t2o - t1o liên hệ với cường độ dòng điện I bằng hệ thức:
\(\Delta {t^0} = t_2^0 - t_1^0 = \dfrac{{{I^2}.R.t}}{{{m_1}{c_1} + {m_2}{c_2}}}\)
Câu hỏi mục 2
Video hướng dẫn giải
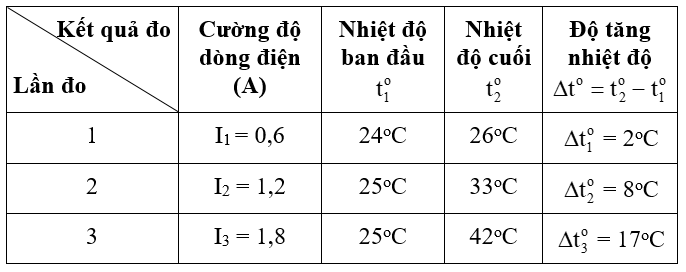
Độ tăng nhiệt độ Δto khi đun nước trong 7 phút với dòng điện có cường dộ khác nhau chạy qua dây đốt.
BẢNG 1
a) Tính tỉ số:
\(\dfrac{{\Delta t_2^0}}{{\Delta t_1^0}} = \dfrac{8}{2} = 4;\dfrac{{I_2^2}}{{I_1^2}} = \dfrac{{1,{2^2}}}{{0,{6^2}}} = 4\)
Ta nhận thấy: \(\dfrac{{\Delta t_2^0}}{{\Delta t_1^0}} = \dfrac{{I_2^2}}{{I_1^2}}\)
b) Tính tỉ số: \(\dfrac{{\Delta t_3^0}}{{\Delta t_1^0}} = \dfrac{{17}}{2} = 8,5;\dfrac{{I_3^2}}{{I_1^2}} = \dfrac{{1,{8^2}}}{{0,{6^2}}} = 9\)
Nếu bỏ qua sai số trong quá trình làm thực nghiệm và sự hao phí nhiệt ra môi trường bên ngoài thì ta có thể coi
\(\dfrac{{\Delta t_3^0}}{{\Delta t_1^0}} = \dfrac{{I_3^2}}{{I_1^2}}\)
Nhiệt lượng tỏa ra ở dây dẫn khi có dòng điện chạy qua tỷ lệ thuận với bình phương cường độ dòng điện chạy qua.
Hệ thức: \(Q = I^2 .R.t\) (trong đó: I là cường độ dòng điện (A), R là điện trở dây dẫn (Q), t là thời gian dòng điện chạy qua (s), Q là nhiệt lượng tỏa ra (J)).
Câu hỏi mục 3
Video hướng dẫn giải
Từ các kết quả trên, hãy phát biểu mỗi quan hệ giữa nhiệt lượng Q tỏa ra trên dây dẫn với cường độ dòng điện I chạy qua nó
Lời giải chi tiết:
Nhiệt lượng Q tỏa ra ở dây dẫn khi có dòng điện chạy qua tỷ lệ thuận với bình phương cường độ dòng điện chạy qua nó.