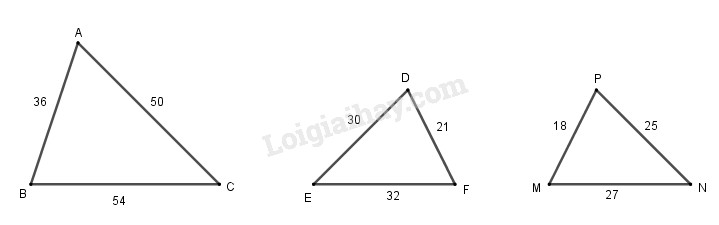
Câu 12.
Trong hình vẽ 27 hai tam giác đồng dạng với nhau là:
A. \(\Delta ABC\) và \(\Delta DEF\)
B. \(\Delta DEF\) và \(\Delta PMN\)
C. \(\Delta PMN\) và \(\Delta ABC\)
Khoanh tròn vào chữ cái trước khẳng định đúng.
Phương pháp giải:
Hai tam giác \(ABC\) và \(A'B'C'\) đồng dạng nếu có \(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}}\).
Lời giải chi tiết:
Ta thấy: \(\dfrac{{PM}}{{AB}} = \dfrac{{PN}}{{AC}} = \dfrac{{MN}}{{BC}} = \dfrac{1}{2}\) nên \(\Delta PMN\) và \(\Delta ABC\) đồng dạng theo tỉ số \(\dfrac{1}{2}\).
Chọn C.
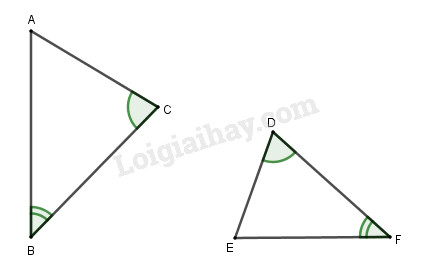
Câu 13.
Trong hình \(28\) cho biết hai tam giác đồng dạng với nhau. Hãy viết các góc tương ứng bằng nhau và các tỉ số bằng nhau vào chỗ trống.
Phương pháp giải:
Sử dụng tính chất của tam giác đồng dạng:
Cho tam giác \(\Delta ABC \backsim \Delta A'B'C'\).
Khi đó \(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}};\) \(\widehat A = \widehat {A'},\widehat B = \widehat {B'},\widehat C = \widehat {C'}\)
Lời giải chi tiết:
\(\begin{array}{l}\widehat A = \widehat E\\\widehat B = \widehat F\\\widehat C = \widehat D\\\dfrac{{AB}}{{EF}} = \dfrac{{AC}}{{DE}} = \dfrac{{BC}}{{DF}}\end{array}\)
soanvan.me
