Đề bài
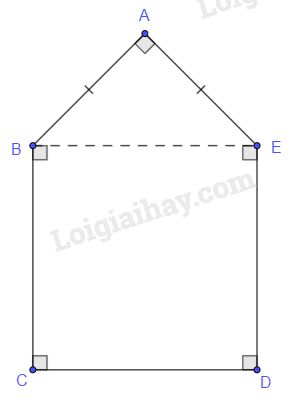
Diện tích đa giác \(ABCD\) trên hình 110 bằng
(A) \(17\) (B) \(18\)
(C) \(20\) (D) \(28\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông.
$$S = {1 \over 2}bc$$
(\(S\) là diện tích; \(b,c\) là hai cạnh của tam giác vuông).
- Diện tích hình vuông cạnh \(a\) bằng \(a^2\).
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết
Áp dụng định lí Pytago vào \(\Delta ABE\) vuông cân tại \(A\) ta có:
\(\eqalign{
& A{B^2} + A{E^2} = B{E^2} \cr
& A{B^2} + A{B^2} = B{E^2} \cr
& 2A{B^2} = {4^2} \cr
& \Rightarrow A{B^2} = 16:2 = 8 \cr
& \Rightarrow AB = 2\sqrt 2 \cr} \)
\(\eqalign{
& {S_{ABE}} = {1 \over 2}AB.AE = {1 \over 2}AB.AB \cr
& \,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}A{B^2} = {1 \over 2}.{\left( {2\sqrt 2 } \right)^2} = 4 \cr
& {S_{BCDE}} = B{C^2} = {4^2} = 16 \cr
& {S_{ABCDE}} = {S_{ABE}} + {S_{BCDE}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\,= 4 + 16 = 20 \cr} \)
Chọn C.
soanvan.me
