Câu 20.
Hai điểm \(A\) và \(B\) đối xứng với nhau qua điểm \(C\) nếu
(A) \(AC=CB\)
(B) điểm \(C\) nằm giữa hai điểm \(A, B\).
(C) có cả hai điều kiện trên.
Khoanh tròn vào chữ cái trước câu trả lời đúng.
Phương pháp giải:
Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
Giải chi tiết:
Chọn C.
Câu 21.
Đúng ghi Đ, sai ghi S vào ô trống
a) Trung điểm của một đoạn thẳng là tâm đối xứng của đoạn thẳng đó.
b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.
c) Giao điểm hai đường chéo của một hình bình hành là tâm đối xứng của hình bình hành đó.
d) Tâm của một đường tròn là tâm đối xứng của đường tròn đó.
Phương pháp giải:
- Định nghĩa: Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)
- Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Giải chi tiết:
a) Đ
b) S
Nếu gọi \(O\) là giao điểm của \(3\) đường trung trực trong \(ΔABC\) (là tam giác đều) thì điểm đối xứng của \(3\) điểm \(A, B, C\) qua \(O\) không thuộc \(ΔABC\) \(\Rightarrow \) Hình này không có tâm đối xứng.
c) Đ
d) Đ
Câu 22.
Đúng ghi Đ, sai ghi S vào ô trống. Cho tam giác vuông \(ABC\) vuông tại \(A\). Gọi \(D,E,M\) theo thứ tự là trung điểm của \(AB, AC,BC.\) Ta có
a) Hai điểm \(A\) và \(B\) đối xứng với nhau qua điểm \(D.\)
b) Hai điểm \(A\) và \(B\) đối xứng với nhau qua đường thẳng \(DM\).
c) Hai điểm \(B\) và \(C\) đối xứng với nhau qua điểm \(E\).
d) Hai điểm \(B\) và \(C\) đối xứng với nhau qua đường thẳng \(AM.\)
Phương pháp giải:
- Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
- Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \( d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa độ dài cạnh ấy.
Giải chi tiết:
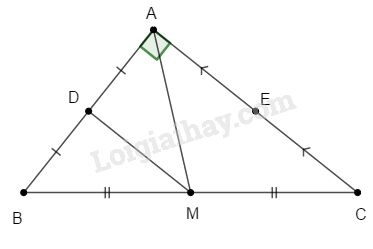
a) Đ
b) Đ
Có \(D,M\) lần lượt là trung điểm của \(AB, BC\) nên \(DM\) là đường trung bình của tam giác \(ABC\)
Suy ra \(DM//AC\), mà \(AC/bot AB\) nên \(DM\bot AB\).
Do đó \(DM\) là đường trung trực của \(AB\) hay hai điểm \(A\) và \(B\) đối xứng với nhau qua đường thẳng \(DM\).
c) S
d) S
Tam giác \(ABC\) không phải là tam giác cân nên \(AM\) không là đường trung trực của \(BC\) nên \(B\) và \(C\) không đối xứng với nhau qua đường thẳng \(AM\).
soanvan.me
