Số nguyên âm và tập hợp các số nguyên

I. Số nguyên âm

1. Cách viết và đọc số nguyên âm

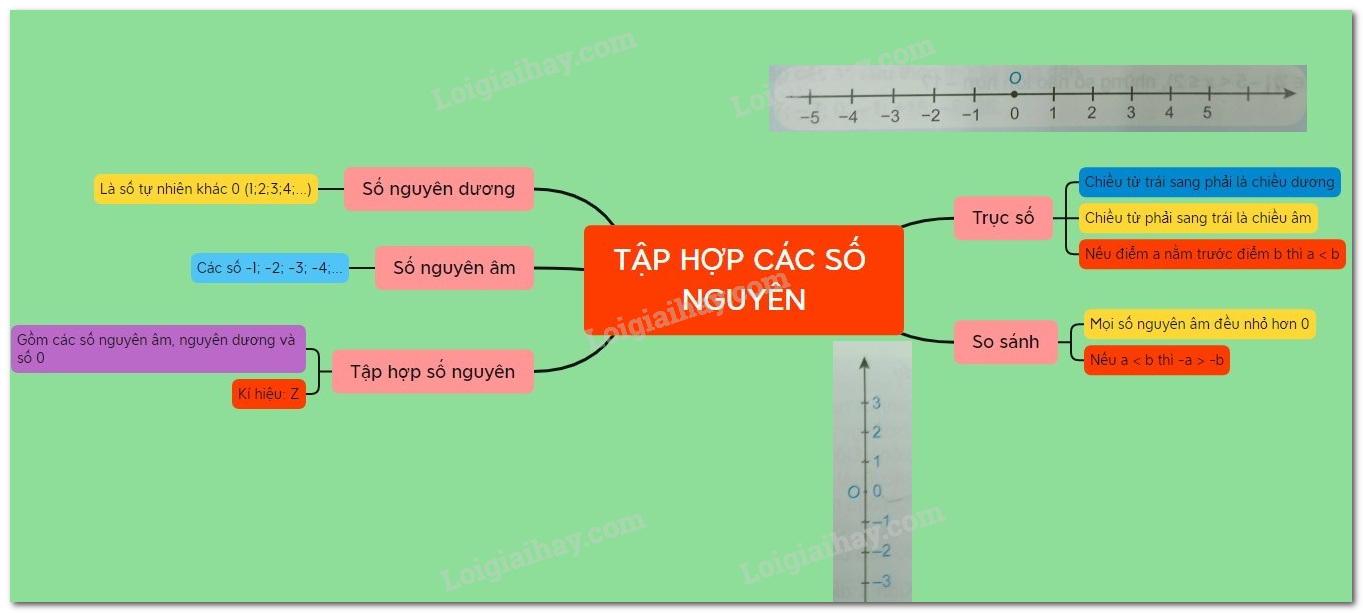
Các số tự nhiên \(1,\,\,2,\,\,3,\,\,4,...\)còn được gọi là các số nguyên dương.

Các số \( - 1,\,\, - 2,\,\, - 3,\,...\) gọi là các số nguyên âm đọc là âm một, âm hai, âm ba,… hoặc trừ một, trừ hai, trừ ba,…

Các số nguyên dương \(1,\,\,2,\,\,3,\,...\) đều mang dấu “+” nên còn được viết được viết là \( + 1,\,\, + 2, + 3,...\)

Cách nhận biết số nguyên âm:

Số nguyên âm được nhận biết bằng dấu “ – “ ở trước số tự nhiên khác 0.

Ví dụ:

\( - 5\) là số nguyên âm, đọc là: âm năm hoặc trừ năm

Âm hai được viết là: \( - 2\).

2. Ứng dụng thực tiễn

Số nguyên âm được sử dụng trong nhiều tình huống thực tiễn cuộc sống:

- Số nguyên âm được dùng để chỉ nhiệt độ dưới \({0^o}C\).

- Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.

- Số nguyên âm được dùng để chỉ số tiền nợ, cũng như để chỉ số tiền lỗ trong kinh doanh.

- Số nguyên âm được dùng để chỉ thời gian trước Công nguyên.

Ví dụ:

+ Bác An nợ \(100\,\,000\) đồng thì ta cũng có thể nói bác An có \( - 100\,\,000\) đồng.

+ Một cơ sở kinh doanh bị lỗ \(30\,\,000\,\,000\) đồng thì ta có thể nói lợi nhuận là: \( - 30\,\,000\,\,000\) đồng.

+ Nhà toán học Py-ta-go sinh năm \( - 570\), nghĩa là ông sinh năm \(570\) trước Công nguyên

+ Nhiệt độ 3 độ dưới \({0^o}C\) được viết là \( - {3^o}C\); đọc là: âm ba độ C.

+ Vùng đất trũng dưới mực nước biển \(5\,\,m\), ta nói độ cao trung bình của vùng đất đó là \( - 5\,\,m\).

II. Tập hợp số nguyên

Chú ý:

Số \(0\) không là số nguyên dương, cũng không là số nguyên âm.

Ví dụ 1:

\(1;\,\,23;\,247;\, - 1;\, - 92;\,- 143\) là các số nguyên.

Ví dụ 2:

Ta có: \( - 3 \in \mathbb{Z};\,\,0 \in \mathbb{Z};\,\,25 \in \mathbb{Z}\).

III. Biểu diễn số nguyên trên trục số

1. Trục số nằm ngang

- Chiều dương hướng từ trái sang phải, chiều ngược lại là chiều âm.

- Điểm gốc của trục số là điểm \(0\).

- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).

- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).

Ví dụ:

Trên trục số đã cho:

+ Điểm \(A\) biểu diễn số \( - 5\).

+ Điểm \(C\) biểu diễn số \( - 1\).

+ Điểm \(M\) biểu diễn số \(2\).

2. Trục số thẳng đứng

- Chiều dương hướng từ dưới lên trên, chiều ngược lại là chiều âm.

- Điểm gốc của trục số là điểm \(0\).

- Điểm biểu diễn số nguyên \(a\) gọi là điểm \(a\).

- Đơn vị đo độ dài trên trục số là độ dài đoạn thẳng nối điểm \(0\) với điểm \(1\).

IV. Số đối của một số nguyên

Chú ý:

- Số đối của một số nguyên dương là một số nguyên âm.

- Số đối của một số nguyên âm là một số nguyên dương.

- Số đối của \(0\) là \(0.\)

Ví dụ:

+ Số đối của \(3\) là \( - 3\).

+ Số đối của \( - 12\) là \(12\).

+ Số đối của 2021 là \( - 2021\).

CÁC DẠNG TOÁN VỀ SỐ NGUYÊN ÂM VÀ TẬP HỢP CÁC SỐ NGUYÊN

I. Dùng số nguyên để diễn tả các tình huống thực tiễn

- Cách dùng để diễn tả nhiệt độ

+ Số nguyên âm được dùng để chỉ nhiệt độ dưới \({0^o}C\).

+ Số nguyên dương được dùng để chỉ nhiệt độ trên \({0^o}C\).

- Cách dùng để chỉ độ cao so với mực nước biển

+ Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.

+ Số nguyên dương được dùng để chỉ độ cao trên mực nước biển.

- Cách dùng để chỉ số tiền lãi (lỗ), số tiền nợ

+ Số nguyên âm được dùng để chỉ số tiền nợ, cũng như chỉ số tiền lỗ trong kinh doanh

+ Số nguyên dương được dùng để chỉ số tiền lãi trong kinh doanh.

- Cách dùng để chỉ thời gian trước và sau công nguyên

+ Số nguyên âm được dùng để chỉ thời gian trước công nguyên.

+ Số nguyên dương được dùng để chỉ thời gian sau công nguyên.

II. Tập hợp số nguyên, phân biệt các số thuộc tập hợp số tự nhiên và số nguyên

Phương pháp: Sử dụng định nghĩa các tập hợp số sau đây:

- Tập hợp số tự nhiên: \(\mathbb{N} = \left\{ {0;\,1;\,2;\,3;....} \right\}\)

- Tập hợp số tự nhiên khác 0: \({\mathbb{N}^*} = \left\{ {1;\,2;\,3;\,....} \right\}\)

- Tập hợp số nguyên: \(\mathbb{Z} = \left\{ {...; - 2;\, - 1;\,0;\,\,1;\,\,2;...} \right\}\)

+ Các số nguyên âm: \( - 1;\, - 2;\, - 3;\, - 4;...\)

+ Các số nguyên dương: \(1;\,2;\,3;\,4;\,...\)

Chú ý: Số 0 không là số nguyên âm cũng không là số nguyên dương.

III. Biểu diễn các số nguyên trên trục số

- Trên trục số nằm ngang:

+ Các điểm biểu diễn số nguyên âm nằm ở bên trái gốc 0

+ Các điểm biểu diễn số nguyên dương nằm ở bên phải gốc 0.

- Trên trục số thẳng đứng:

+ Các điểm biểu diễn số nguyên âm nằm ở bên dưới gốc 0

+ Các điểm biểu diễn số nguyên dương nằm ở bên trên gốc 0.

IV. Tìm số đối của một số nguyên cho trước

Phương pháp:

- Hai số đối nhau chỉ khác nhau về dấu.

- Số đối của $0$ là $0.$

Ví dụ: