Đề bài
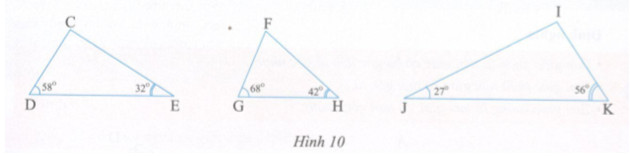
1. Trong các tam giác ở hình 10, tam giác nào là tam giác nhọn, tam giác nào là tam giác tù, tam giác nào là tam giác vuông ?
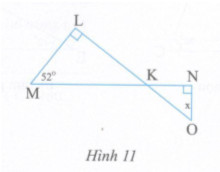
2. Tìm số đo x ở hình 11:
Lời giải chi tiết
1.
\(\Delta CDE\) có \(\widehat C + \widehat D + \widehat E = {180^0}.\) Mà \(\widehat D = {58^0}(gt),\widehat E = {32^0}(gt)\)
Do đó: \(\widehat C + {58^0} + {32^0} = {180^0} \Rightarrow \widehat C = {180^0} - {58^0} - {32^0} = {90^0}.\)
Vậy tam giác CDE vuông tại C.
Tam giác FGH có \(\widehat F + \widehat G + \widehat H = {180^0}.\) Mà \(\widehat G = {68^0}(gt),\widehat H = {42^0}(gt)\)
Do đó: \(\widehat F + {68^0} + {42^0} = {180^0} \Rightarrow \widehat F = {180^0} - {68^0} - {42^0} = {70^0}\)
Vậy tam giác FGH là tam giác nhọn.
Tam giác IJK có \(\widehat I + \widehat J + \widehat K = {180^0}\)
Mà \(\widehat J = {27^0},\widehat K = {56^0}.\) Do đó: \(\widehat I + {27^0} + {56^0} = {180^0} \Rightarrow \widehat I = {180^0} - {27^0} - {56^0} = {97^0}\)
Vậy tam giác IJK là tam giác tù.
2.
Tam giác LMK vuông tại L nên \(\widehat M + \widehat {LKM} = {90^0} \Rightarrow \widehat M = {90^0} - \widehat {LKM}(1)\)
Tam giác NKO vuông tại N nên \(\widehat {NOK} + \widehat {NKO} = {90^0} \Rightarrow \widehat {NOK} = {90^0} - \widehat {NKO}(2)\)
Mà \(\widehat {LKM} = \widehat {NKO}\) (đối đỉnh) (3)
Từ (1), (2), (3) ta có: \(\widehat {NOK} = \widehat {M.}\) Vậy \(x = \widehat {NOK} = \widehat M = {52^0}.\)
soanvan.me
