Đề bài
Cho đường tròn (O), bán kính OM = 8 cm, điểm I thuộc đoạn OM sao cho IO = 2IM. Từ I kẻ đường thẳng vuông góc với OM cắt đường tròn tại A và B. Tính AB.
Lời giải chi tiết
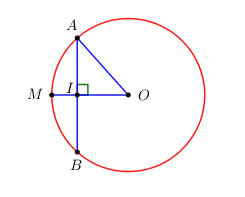
Ta có \(OI = 2IM \)
\(\Rightarrow OI = \dfrac{2}{3}OM = \dfrac{2}{3}.8 = \dfrac{{16}}{3}\,\,\left( {cm} \right)\)
Áp dụng định lí Pytago trong tam giác vuông OAI có :
\(AI = \sqrt {O{A^2} - O{I^2}} = \sqrt {{8^2} - {{\left( {\dfrac{{16}}{3}} \right)}^2}} \)\(\,= \sqrt {\dfrac{{320}}{9}} = \dfrac{{8\sqrt 5 }}{3}\) (cm)
Lại có \(OM \bot AB \Rightarrow \) I là trung điểm của \(AB\) (quan hệ vuông góc giữa đường kính và dây cung)
\( \Rightarrow AB = 2AI = 2.\dfrac{{8\sqrt 5 }}{3} = \dfrac{{16\sqrt 5 }}{3}\,\,\left( {cm} \right)\).
soanvan.me
