Đề bài
Dựng hình thang ABCD, biết \(\widehat D = {90^o}\) , đáy CD = 3 cm, cạnh bên AD = 2 cm, cạnh bên \(BC = 3 cm.\)
Lời giải chi tiết
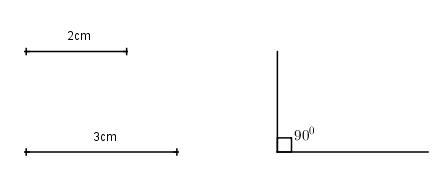
a) Phân tích:
Giả sử dựng được hình thang ABCD thỏa mãn yêu cầu của đề bài.
Ta thấy tam giác ACD dựng được vì biết hai cạnh và góc xen giữa.
Điểm B phải thỏa mãn hai điều kiện:
- B nằm trên đường thẳng qua A và song song với CD.
- B nằm trên đường tròn tâm C bán kính 3cm
b) Cách dựng
- Dựng \(\Delta ACD\) có \(AD = 2cm,\,\,CD = 3cm,\,\,\widehat D = {90^0}\)
- Dựng tia Ax song song với CD (tia Ax và điểm C nằm trong cùng một nửa mặt phẳng bờ AD)
- Dựng cung tròn tâm C bán kính 3cm. B là giao điểm của cung tròn này với tia Ax. Kẻ đoạn thẳng BC.
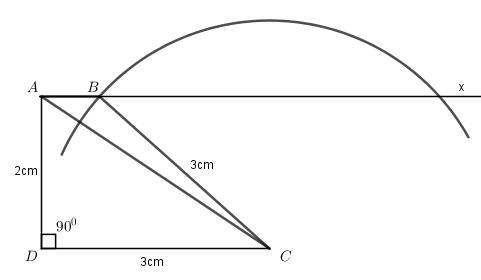
c) Chứng minh
Tứ giác ABCD là hình thang vì có AB // CD, \(AD = 2cm,\,\,CD = 3cm,\,\,\widehat D = {90^0}\) (theo bước dựng 1), \(BC = 3cm\) (vì B thuộc đường tròn tâm C bán kính 3cm)
d) Biện luận
Dựng được hai điểm B trên tia Ax
Ta luôn luôn dựng được hai hình thang thỏa mãn điều kiện của đề bài.
soanvan.me
