Đề bài
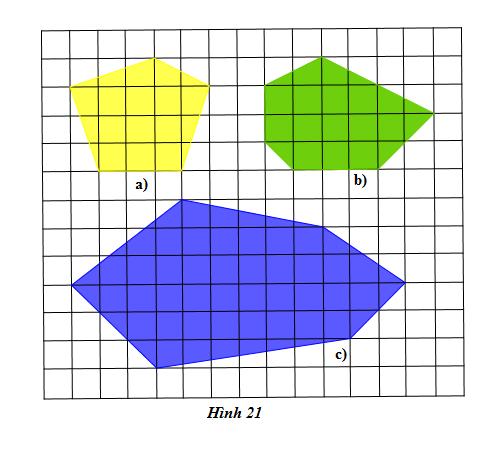
Cho biết cạnh mỗi ô vuông trên hình 21 là 1 m. Tính và ghi diện tích của mỗi hình bên ngay trên hình.
Lời giải chi tiết
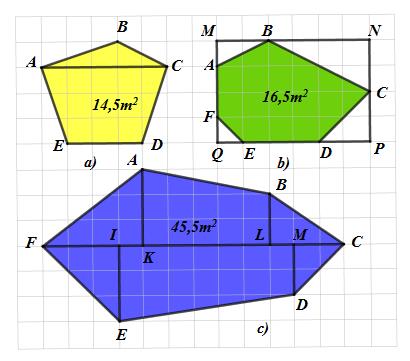
* Diện tích đa giác ABCDE trên hình a bằng tổng diện tích của các tam giác ABC và hình thang ACDE.
\(\eqalign{ & {S_{ABC}} = {1 \over 2}.5.1 = 2,5\,\,\left( {c{m^2}} \right) \cr & {S_{ACDE}} = {1 \over 2}\left( {3 + 5} \right).3 = 12 \cr} \)
Do đó \({S_{ABCDE}} = {S_{ABC}} + {S_{ACDE}} = 2,5 + 12 = 14,5\,\,\left( {{m^2}} \right)\)
* Diện tích đa giác ABCDEF trên hình b bằng diện tích của hình chữ nhật MNPQ trừ đi diện tích tam giác ABM, BCN, CDP, EFQ.
\(\eqalign{ & {S_{MNPQ}} = 6.4 = 24\,\,\left( {{m^2}} \right) \cr & {S_{ABM}} = {1 \over 2}.2.1 = 1\,\,\left( {{m^2}} \right) \cr & {S_{BCN}} = {1 \over 2}.3.2 = 3\,\,\left( {{m^2}} \right) \cr & {S_{CDP}} = {1 \over 2}.2.2 = 2\,\,\left( {{m^2}} \right) \cr & {S_{EFQ}} = {1 \over 2}.1.1 = 0,5\,\,\left( {{m^2}} \right) \cr} \)
Do đó
\(\eqalign{ & {S_{ABCDEF}} = {S_{MNPQ}} - {S_{ABM}} - {S_{BCN}} - {S_{CDP}} - {S_{EFQ}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 24 - 1 - 3 - 2 - 0,5 = 17,5\,\,\left( {{m^2}} \right) \cr} \)
* Diện tích của đa giác ABCDEF trên hình c bằng tổng diện tích các tam giác KAF, LBC, MCD, IEF và diện tích hai hình thang AKLB, EIMD.
\(\eqalign{ & {S_{KAF}} = {1 \over 2}.3.4 = 6\,\,\left( {{m^2}} \right) \cr & {S_{LBC}} = {1 \over 2}.2.3 = 3\,\,\left( {{m^2}} \right) \cr & {S_{MCD}} = {1 \over 2}.2.2 = 2\,\,\left( {{m^2}} \right) \cr & {S_{IEF}} = {1 \over 2}.3.3 = 4,5\,\,\left( {{m^2}} \right) \cr & {S_{AKLB}} = {1 \over 2}\left( {3 + 2} \right).5 = 12,5\,\,\left( {{m^2}} \right) \cr & {S_{EIMD}} = {1 \over 2}\left( {3 + 2} \right).7 = 17,5\,\,\left( {{m^2}} \right) \cr} \)
Do đó
\(\eqalign{ & {S_{ABCDEF}} = {S_{KAF}} + {S_{LBC}} + {S_{MCD}} + {S_{IEF}} + {S_{AKLB}} + {S_{EIMD}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 6 + 3 + 2 + 4,5 + 12,6 + 17,5 = 45,5\,\,\left( {{m^2}} \right) \cr} \)
soanvan.me
