Đề bài
Tìm a để đa thức \(({x^2} + 2x + a)\) chia hết cho đa thức \((x - 1)\) .
Lời giải chi tiết
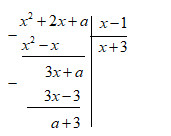
Để chia hết thì đa thức dư phải bằng 0 với mọi giá trị x.
Do đó \(a + 3 = 0 \Leftrightarrow a = - 3\). Vậy \(a = - 3\) thì \({x^2} + 2x + a\) chia hết cho \(x - 1\)
Cách 2:
Gọi thương khi chia \({x^2} + 2x + a\) cho \(x - 1\) là \(Q\left( x \right)\), ta có: \({x^2} + 2x + a = \left( {x - 1} \right)Q\left( x \right)\)
Vì đẳng thức trên đúng với mọi x nên cho \(x = 1\)
Ta có: \({1^2} + 2.1 + a = 0 \Rightarrow 3 + a = 0 \Rightarrow a = - 3\)
Vậy với \(a = - 3\) thì \({x^2} + 2x + a\) chia hết cho \(x - 1\).
Cách 3:
Đa thức bị chia có bậc hai, đa thức chia có bậc một nên thương là một nhị thức bậc nhất, có hạng tử bậc nhất là \({x^2}:x = x\).
Gọi thương là \(x + b\), ta có:
\(\eqalign{ & {x^2} + 2x + a = \left( {x - 1} \right)\left( {x + b} \right) \cr & {x^2} + 2x + a = {x^2} + bx - x - b \cr & {x^2} + 2x + a = {x^2} + \left( {b - 1} \right)x - b \cr} \)
Do đó \(2 = b - 1\) và \(a = - b \Rightarrow b = 3\) và \(a = - b\)
Nên \(a = - 3\).
Vậy với \(a = - 3\) thì \({x^2} + 2x + a\) chia hết cho \(x - 1\).
soanvan.me
