Đề bài
Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh \(AB, BC, AC.\) Cho biết \(OD > OE, OE = OF\) (h.69).
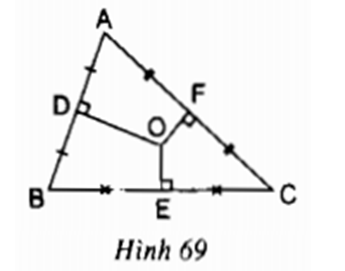
Hãy so sánh các độ dài:
a) BC và AC;
b) AB và AC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng:
Trong hai dây của một đường tròn:
+ Hai dây cách đều tâm thì bằng nhau
+ Dây nào xa tâm hơn thì dây đó nhỏ hơn
Lời giải chi tiết
Vì O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
a) Vì \(OE = OF \) suy ra \(AC=BC\) (hai dây cách đều tâm thì bằng nhau)
b) Vì \(OD > OE\) nên \(AB < BC\) (dây nào gần tâm hơn thì dây đó lớn hơn) mà \(AC=BC\) (câu a) nên \(AB<AC.\)
