Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ , chọn khẳng định đúng.
-
A
\(AC'\) và \(DB'\) cắt nhau
-
B
\(AC'\) và $BC$ cắt nhau
-
C
$AC$ và $DB$ không cắt nhau
-
D
$AB$ và $CD$ cắt nhau.
Đáp án của giáo viên lời giải hay : A
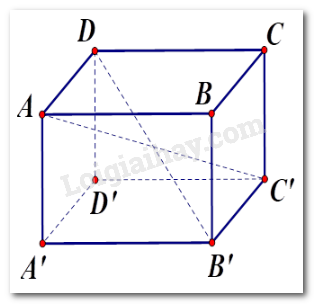
Ta có $AC'$ cắt $DB'$ vì $AD$ // $B'C'$ , $AD = B'C'$ nên $ADC'B'$ là hình bình hành, do đó $AC'$ cắt $DB'$ nên A đúng.
$AC'$ không cắt $BC$ vì chúng không có điểm chung nên B sai.
$AB$ và $CD$ song song nên chúng không cắt nhau nên D sai.
$AC$ và $BD$ cắt nhau nên C sai.
Hãy kể tên các mặt của hình hộp chữ nhật $ABCD.A'B'C'D'$. Hãy chọn câu sai
-
A
mp $\left( {ABCD} \right)$.
-
B
mp $\left( {A'B'C'D'} \right)$.
-
C
mp $\left( {ABB'A'} \right)$.
-
D
mp $\left( {AB'C'D} \right)$.
Đáp án của giáo viên lời giải hay : D
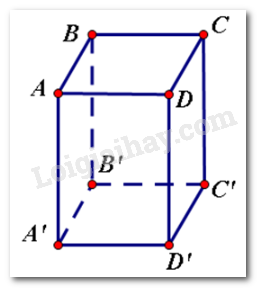
Hình hộp chữ nhật gồm $6$ mặt:
\(\left( {ADD'A'} \right);\,\left( {DCC'D'} \right);\left( {BCC'B'} \right);\,\left( {ABB'A'} \right);\,\left( {ABCD} \right);\left( {A'B'C'D'} \right)\)
Hãy chọn câu sai. Hình hộp chữ nhật $ABCD.{\rm{ }}A'B'C'D'$ có
-
A
$8$ đỉnh.
-
B
$12$ cạnh.
-
C
$6$ cạnh.
-
D
$6$ mặt.
Đáp án của giáo viên lời giải hay : C
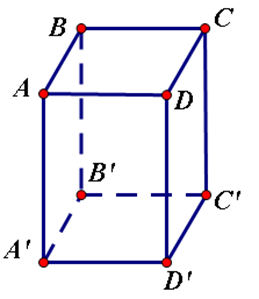
Hình hộp chữ nhật có \(12\) cạnh:
\(\begin{array}{l}AB;BC;CD;DA;A'B';C'D';\\B'C';D'A';AA';BB';CC';DD'\end{array}\)
Nên C sai.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Gọi tên mặt phẳng chứa đường thẳng $A'B$ và $CD'$. Hãy chọn câu đúng.
-
A
mp$\left( {ABB'A'} \right)\;\;\;$.
-
B
mp $\left( {ADD'A'} \right)$.
-
C
mp $\left( {DCC'D'} \right)\;\;\;$.
-
D
mp $\left( {A'BCD'} \right)\;\;\;$.
Đáp án của giáo viên lời giải hay : D
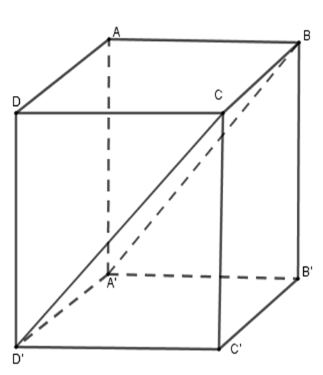
Mặt phẳng chứa đường thẳng \(A'B\) và \(CD'\) là mặt phẳng đi qua bốn điểm \(A',\,B,\,C,\,D'\) hay chính là $mp \left( {A'BCD'} \right).$
Hãy kể tên những cạnh bằng nhau của hình hộp chữ nhật $ABCD.A'B'C'D'$.
Hãy chọn câu sai
-
A
$AB = A'B'$.
-
B
$DC = D'C'\;\;\;$.
-
C
$AB{\rm{ }} = {\rm{ }}C'D'\;\;$.
-
D
$DC{\rm{ }} = {\rm{ }}DD'$.
Đáp án của giáo viên lời giải hay : D
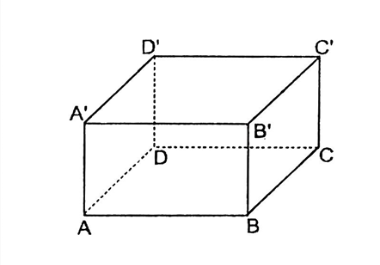
Các cạnh bằng nhau của hình hộp chữ nhật \(AA' = BB' = CC' = DD'\) ; \(AB = DC = A'B' = D'C'\) ;
\(AA' = BB' = CC' = DD'\) .
Nên D sai.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Có bao nhiêu cạnh cắt cạnh $AB$
-
A
$4$.
-
B
$3$.
-
C
$2$.
-
D
$5$.
Đáp án của giáo viên lời giải hay : A
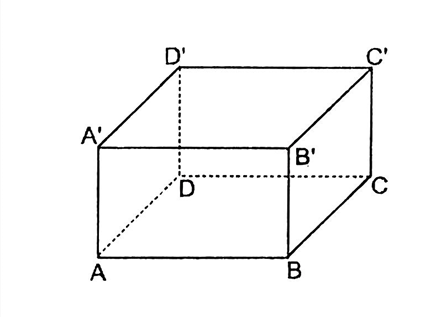
Có bốn cạnh cắt $AB$ là $AD,AA',BC,BB'.$
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Có bao nhiêu cạnh song song với cạnh $AB$
-
A
$4$.
-
B
$3$.
-
C
$2$.
-
D
$5$.
Đáp án của giáo viên lời giải hay : B
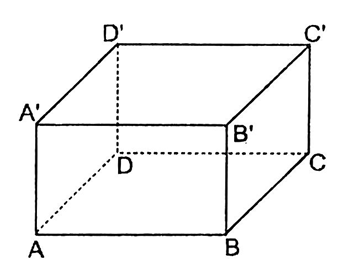
Có ba cạnh song song với $AB$ là $A'B',CD,C'D'$ .
Trong các mặt của một hình hộp chữ nhật, tính số cặp mặt song song với nhau là
-
A
$4$.
-
B
$2$.
-
C
$3$.
-
D
$0$.
Đáp án của giáo viên lời giải hay : C
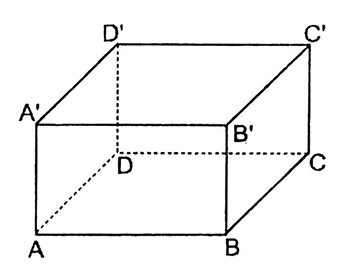
Có $3$ cặp mặt phẳng song song là mp \(\left( {ABB'A'} \right)\) và mp \(\left( {DCC'D'} \right)\) ; mp \(\left( {ABCD} \right)\) và mp \(\left( {A'B'C'D'} \right)\); mp \(\left( {ADD'A'} \right)\) và mp \(\left( {BCC'B'} \right)\)
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Gọi $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$ theo thứ tự là trung điểm $AA',{\rm{ }}BB',{\rm{ }}CC',{\rm{ }}DD'$. Hãy chọn câu sai
-
A
Bốn điểm $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$cùng thuộc một mặt phẳng.
-
B
mp $\left( {MNIK} \right)$// mp $\left( {ABCD} \right)$.
-
C
mp $\left( {MNIK} \right)$ // mp $\left( {A'B'C'D'} \right)$.
-
D
mp $\left( {MNIK} \right)$ // mp $\left( {ABB'A'} \right)$.
Đáp án của giáo viên lời giải hay : D
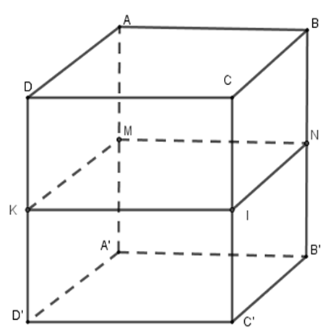
Vì $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$ theo thứ tự là trung điểm $AA',{\rm{ }}BB',{\rm{ }}CC',{\rm{ }}DD'$ nên \(KM = IN;\,KM{\rm{//}}IN\)
Suy ra bốn điểm $M,{\rm{ }}N,{\rm{ }}I,{\rm{ }}K$ cùng thuộc một mặt phẳng.
Lại có \(KM{\rm{//}}AD{\rm{//}}A'D'\) nên mp $\left( {MNIK} \right)$// mp $\left( {ABCD} \right)$ và mp $\left( {MNIK} \right)$// mp $\left( {A'B'C'D'} \right)$
Ta thấy mp \(\left( {MNIK} \right)\) và mp \(\left( {ABB'A'} \right)\) cắt nhau theo đường thẳng \(MN\) nên chúng không song song.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $O$ và $O'$ lần lượt là tâm \(ABCD;\,A'B'C'D'\) . Hai mp $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường nào?
-
A
$OO'$.
-
B
$CC'$.
-
C
$AD$.
-
D
$AO$.
Đáp án của giáo viên lời giải hay : A
Tìm đoạn thẳng thuộc cả hai mặt phẳng.
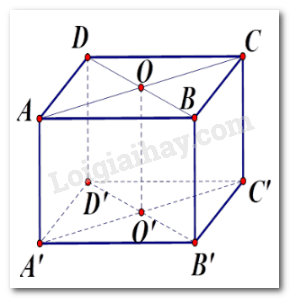
Gọi $O$ là giao điểm của $AC$ và $BD$ . Ta có \(O \in AC\) nên \(O \in {\rm{mp}}\left( {ACC'A'} \right)\), \(O \in BD\) nên \(O \in {\rm{mp}}\left( {BDD'B'} \right)\), do đó $O$ thuộc cả hai mặt phẳng trên. (1)
Gọi \(O'\) là giao điểm của \(A'C'\) và \(B'D'\) .
Chứng minh tương tự, \(O'\) thuộc cả hai mặt phẳng trên. (2)
Từ (1) và (2) suy ra hai mặt phẳng $(ACC'A')$ và mp $\left( {BDD'B'} \right)$ cắt nhau theo đường thẳng \(OO'\) .
Cho hình lập phương $ABCD.A'B'C'D'$. Tính số đo góc \(AB'C\) .
-
A
$90^\circ $.
-
B
$45^\circ $.
-
C
$30^\circ $.
-
D
$60^\circ $.
Đáp án của giáo viên lời giải hay : D
Mối quan hệ giữa các cạnh trong hình hộp chữ nhật từ đó suy ra số đo góc.
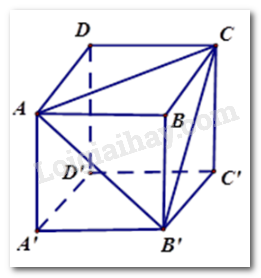
Các tam giác $ABC,ABB',CBB'$ vuông cân nên $AC = AB' = B'C$ .
Tam giác $AB'C$ có ba cạnh bằng nhau nên là tam giác đều, suy ra \(\widehat {AB'C} = {60^0}\) .
Tình độ dài của một chiếc hộp hình lập phương, biết rằng nếu độ dài mỗi cạnh của hộp tang thêm $2\,cm$ thì diện tích phải sơn $6$ mặt bên ngoài của hộp đó tăng thêm $216\,c{m^2}$ .
-
A
$4\,cm$.
-
B
$8\,cm$.
-
C
$6\,cm$.
-
D
$5\,cm$.
Đáp án của giáo viên lời giải hay : B
+ Gọi độ dài hình lập phương là \(x\) , dựa vào dữ kiện đề bài để suy ra phương trình ẩn \(x\) .
+ Giải phương trình ta tìm được cạnh của hình lập phương
Diện tích phải sơn một mặt của hình hộp tăng thêm \(216:6 = 36\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Gọi độ dài cạnh của hình lập phương là $x\,\left( {cm} \right)$ , \(x > 0\)
Phương trình \({\left( {x + 2} \right)^2} - {x^2} = 36\)
\( \Leftrightarrow {x^2} + 4x + 4 - {x^2} = 36\)
\(\Leftrightarrow 4x = 32\)
\(\Leftrightarrow x = 8\) (TM )
Độ dài cạnh của chiếc hộp bằng $8cm$ .
