Cho hai đường thẳng \(a;b.\) Khi đó \(a;b\) có thể
-
A
Song song
-
B
Trùng nhau
-
C
Cắt nhau
-
D
Cả ba đáp án trên đều đúng
Đáp án của giáo viên lời giải hay : D
Vị trí của hai đường thẳng:
Hai đường thẳng $a,{\rm{ }}b$ bất kì có thể:
+ Trùng nhau: có vô số điểm chung.
+ Cắt nhau: chỉ có $1$ điểm chung - điểm chung đó gọi là giao điểm.
+ Song song: không có điểm chung nào.
Hai đường thẳng \(a,b\) bất kì có thể trùng nhau, song song hoặc cắt nhau.
Chọn câu đúng.
-
A
Qua hai điểm phân biệt có vô số đường thẳng
-
B
Có vô số điểm cùng thuộc một đường thẳng
-
C
Hai đường thẳng phân biệt thì song song
-
D
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa
Đáp án của giáo viên lời giải hay : B
Nhận xét tính đúng sai của từng đáp án dựa vào các kiến thức về sự xác định đường thẳng đi qua hai điểm, số điểm thuộc đường thẳng, vị trí tương đối của hai đường thẳng, vị trí của ba điểm thẳng hàng.
Đáp án A: Qua hai điểm phân biệt có một và chỉ một đường thẳng nên A sai.
Đáp án B: Có vô số điểm cùng thuộc một đường thẳng nên B đúng.
Đáp án C: Hai đường thẳng phân biệt thì có thể song song hoặc cắt nhau nên C sai.
Đáp án D: Trong ba điểm thẳng hàng chỉ có một điểm nằm giữa hai điểm còn lại nên D sai.
Cho $3$ đường thẳng $a,{\rm{ }}b,{\rm{ }}c$ phân biệt. Trong trường hợp nào thì ba đường thẳng đó đôi một không có giao điểm?
-
A
ba đường thẳng đôi một cắt nhau
-
B
\(a\) cắt \(b\) và \(a\) song song \(c\)
-
C
ba đường thẳng đôi một song song
-
D
\(a\) song song \(b\) và \(a\) cắt \(c\)
Đáp án của giáo viên lời giải hay : C
Sử dụng các vị trí của hai đường thẳng phân biệt:
+ Cắt nhau: chỉ có 1 điểm chung - điểm chung đó gọi là giao điểm.
+ Song song: không có điểm chung nào.
Ba đường thẳng đôi một không có giao điểm nghĩa là:
+ \(a,b\) không có giao điểm hay \(a\) song song \(b\)
+ \(b,c\) không có giao điểm hay \(b\) song song \(c\)
+ \(a,c\) không có giao điểm hay \(a\) song song \(c\)
Vậy ba đường thẳng đôi một song song.
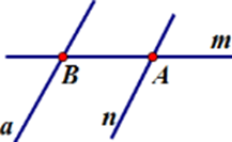
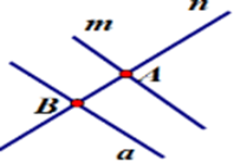
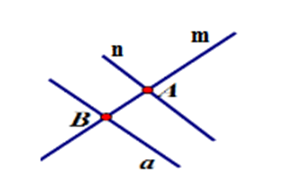
Cho đường thẳng $m$ và đường thẳng $n$ cắt nhau tại $A,$ đường thẳng $a$ không cắt đường thẳng $m$ nhưng cắt đường thẳng $n$ tại $B.$ Hãy chọn hình vẽ đúng trong các hình sau?
-
A
-
B

-
C
-
D
Đáp án của giáo viên lời giải hay : C
Quan sát các hình vẽ ở từng đáp án, so sánh với các dữ kiện bài cho và kết luận.
Sử dụng lý thuyết về vị trí của hai đường thẳng:
+ Cắt nhau: chỉ có 1 điểm chung - điểm chung đó gọi là giao điểm.
+ Song song: không có điểm chung nào.
Hình A: Có đường thẳng $m$ cắt đường thẳng $n$ tại $A,$ đường thẳng $a$ cắt đường thẳng $m$ tại $B$ nhưng không cắt đường thẳng $n$ (trái với đề bài là $a$ cắt $n$ tại $B$ ) (loại)
Hình B: Đường thẳng $m$ cắt đường thẳng $n$ tại $A,{\rm{ }}a$ cắt m tại $C,$ cắt $n$ tại $B$ (trái với đề bài là $a$ không cắt $m$) (loại)
Hình C: Đường thẳng $m$ cắt đường thẳng $n$ tại $A,$ đường thẳng $a$ cắt đường thẳng $n$ tại $B$ và $a$ không cắt $m$ (thỏa mãn)
Hình D: Đường thẳng $a$ cắt đường thẳng $m$ tại $B$ (trái với đề bài là \(a\) không cắt \(m\)) (loại)
Chọn hình vẽ có hai đường thẳng vuông góc với nhau:

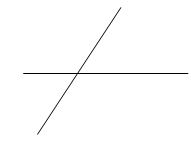
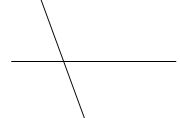


Quan sát hình vẽ để xác định hai đường thẳng vuông góc với nhau.
Quan sát các hình đã cho ta thấy hình thứ nhất có hai đường thẳng vuông góc với nhau.
Chọn hình vẽ có hai đường thẳng song song với nhau:





Quan sát hình vẽ để xác định hai đường thẳng song song với nhau.
Quan sát các hình đã cho ta thấy hình thứ ba từ trên xuống dưới có hai đường thẳng song song với nhau.
 Cho hình vẽ như sau:
Cho hình vẽ như sau:
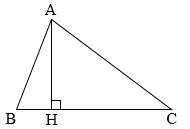
Cạnh AH vuông góc với cạnh nào dưới đây?
A. BH, HC và BC
B. BH và AC
C. AB, AC và HC
D. AB và AC
A. BH, HC và BC
Quan sát hình vẽ để xác định các cạnh vuông góc với nhau.
Quan sát hình vẽ ta thấy AH vuông góc với các cạnh là HB, HC và BC.
Điền số thích hợp vào ô trống:
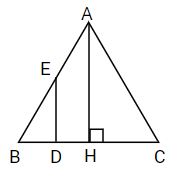
Trong hình đã cho có
cặp cạnh song song với nhau.
Trong hình đã cho có
cặp cạnh song song với nhau.
Quan sát hình vẽ để xác định cặp cạnh song song với nhau.
Trong hình trên có ED song song với AH.
Vậy hình đã cho có \(1\) cặp cạnh song song với nhau.
Đáp án đúng điền vào ô trống là \(1\) .
Cho hình vẽ như sau :
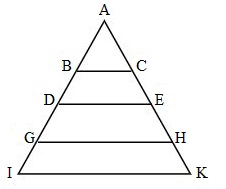
Cạnh DE song song với mấy cạnh, đó là những cạnh nào?
A. \(2\) cạnh, đó là BC, AI
B. \(2\) cạnh, đó là IK, EK
C. \(3\) cạnh, đó là BC, GH, IK
D. \(4\) cạnh, đó là BC, GH, AD, EK
C. \(3\) cạnh, đó là BC, GH, IK
Quan sát hình vẽ để xác định các cạnh song song với nhau.
Quan sát hình ta thấy cạnh DE song song với \(3\) cạnh là BC, GH, IK.
Điền số thích hợp vào ô trống:
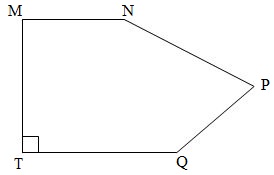
Trong hình có
cặp cạnh vuông góc với nhau,
cặp cạnh song song.
Trong hình có
cặp cạnh vuông góc với nhau,
cặp cạnh song song.
Quan sát hình vẽ để xác định các cặp cạnh vuông góc và các cặp cạnh song song.
Hình đã cho có:
- \(2\) cặp cạnh vuông góc là MN và MT; TM và TQ.
- \(1\) cặp cạnh song song là MN và TQ.
Vậy đáp án đúng điền vào ô trống lần lượt từ trái sang phải là \(2\,\,;\,\,1\).
Cho hình vẽ như sau:
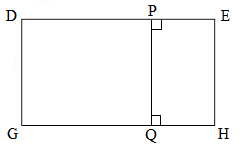
Cạnh PQ vuông góc với những cạnh nào?
A. Cạnh PE, PD
B. Cạnh QH, QG
C. Cạnh DE, GH
D. Tất cả các đáp án trên đều đúng
D. Tất cả các đáp án trên đều đúng
Quan sát hình vẽ để xác định các cặp cạnh vuông góc với nhau.
Quan sát hình vẽ ta thấy cạnh PQ vuông góc với các cạnh là PE, PD, QH, QG, DE, GH.
Cho hình vẽ sau:
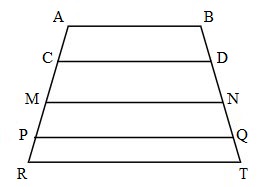
Trong hình trên có bao nhiêu cặp cạnh song song với nhau?
A. \(10\) cặp
B. \(9\) cặp
C. \(8\) cặp
D. \(7\) cặp
A. \(10\) cặp
Quan sát hình vẽ để xác định các cặp cạnh song song với nhau.
Hình vẽ đã cho có:
- Cạnh AB song song với cạnh CD.
- Cạnh AB song song với cạnh MN .
- Cạnh AB song song với cạnh PQ.
- Cạnh AB song song với cạnh RT.
- Cạnh CD song song với cạnh MN.
- Cạnh CD song song với cạnh PQ.
- Cạnh CD song song với cạnh RT .
- Cạnh MN song song với cạnh PQ.
- Cạnh MN song song với cạnh PT.
- Cạnh PQ song song với cạnh RT.
Vậy trong hình đã cho có \(10\) cặp cạnh song song với nhau.
