Các mặt bên của hình lăng trụ đứng là
-
A
Các hình bình hành
-
B
Các hình thang cân
-
C
Các hình chữ nhật
-
D
Các hình vuông
Đáp án của giáo viên lời giải hay : C
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Các cạnh bên của hình lăng trụ đứng
-
A
Song song với nhau
-
B
Bằng nhau
-
C
Vuông góc với hai đáy
-
D
Có cả ba tính chất trên
Đáp án của giáo viên lời giải hay : D
Hình lăng trụ đứng có các mặt bên là hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau.
Cho hình lăng trụ đứng $ABCD.A'B'C'D'$ có đáy $ABCD$ là hình thang vuông \(\left( {\widehat A = \widehat B = {{90}^0}} \right)\) .
Có bao nhiêu cạnh song song với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A
\(1\)
-
B
\(2\)
-
C
\(4\)
-
D
\(5\)
Đáp án của giáo viên lời giải hay : C
Sử dụng quan hệ song song giữa đường thẳng và mặt phẳng.
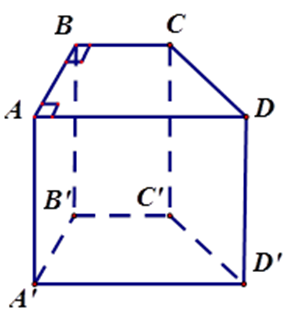
Vì $AA'{\rm{//}}BB'{\rm{//}}DD'$ và \(A'D'{\rm{//}}AD{\rm{//}}BC\) nên các đường thẳng $AA',DD',AD,A'D'$ song song với mp $\left( {BCC'B'} \right).$
Có bao nhiêu cạnh vuông góc với mặt phẳng \(\left( {BCC'B'} \right)\) ?
-
A
\(1\)
-
B
\(2\)
-
C
\(4\)
-
D
\(5\)
Đáp án của giáo viên lời giải hay : B
Sử dụng quan hệ vuông góc giữa đường thẳng và mặt phẳng.
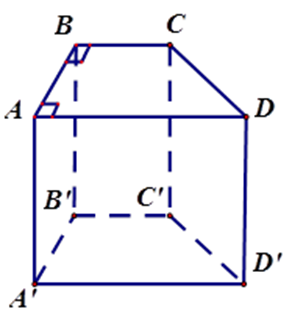
Vì \(AB \bot BC\) (do \(ABCD\) là hình thang vuông) và \(AB \bot BB'\) (tính chất lăng trụ đứng)
Nên \(AB \bot \left( {BCC'B'} \right)\) , tương tự ta có \(A'B' \bot \left( {BCC'B'} \right)\)
Do đó $AB,A'B'$ vuông góc với mp $\left( {BCC'B'} \right).$
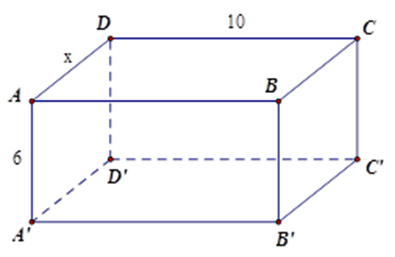
Một hình hộp chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng $6\,cm$ . Một kích thước của đáy bằng $10\,cm$ , tính kích thước còn lại.
-
A
\(15\,cm\)
-
B
\(20\,cm\)
-
C
\(25\,cm\)
-
D
\(10\,cm\)
Đáp án của giáo viên lời giải hay : A
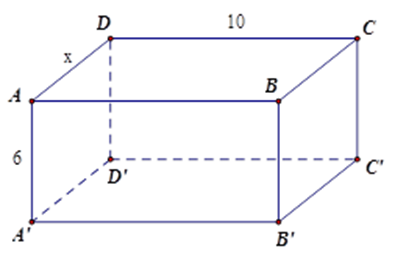
Đặt $AD = x$ .
Diện tích xung quanh bằng:
$2\left( {10 + x} \right).6\left( {c{m^2}} \right)$
Tổng diện tích hai đáy bằng $2.10x\left( {c{m^2}} \right)$
Ta có $2\left( {10 + x} \right).6{\rm{ }} = {\rm{ }}2.10x \Leftrightarrow 60 + 6x = 10x \Leftrightarrow x = 15$
Kích thước còn lại của đáy bằng $15cm$ .
Một hình hộp chữ nhật có diện tích xung quanh bằng $120\,c{m^2}$ , chiều cao bằng $6cm$ . Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
-
A
\(8\,cm\)
-
B
\(7\,cm\)
-
C
\(6\,cm\)
-
D
\(5\,cm\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng công thức thể tích và diện tích xung quanh của hình hộp chữ nhật.
+ Dùng hằng đẳng thức để biện luận theo yêu cầu đề bài.
Gọi $a$ và $b$ là các kích thước của đáy.
Ta có $V = 6ab$ nên $V$ lớn nhất \( \Leftrightarrow \) $ab$ lớn nhất
\({S_{xq}} = 120\) nên \(2\left( {a + b} \right).6 = 120\) hay \(a + b = 10\).
Ta có: \(ab = a\left( {10 - a} \right) = - {a^2} + 10a = - {\left( {a - 5} \right)^2} + 25 \le 25\).
Suy ra \(V = 6ab \le 6.25 = 150\).
Thể tích lớn nhất bằng \(150\) \({\rm{c}}{{\rm{m}}^3}\) khi \(a = b = 5\), tức là các cạnh đáy bằng $5$ cm.
Tính thể tích của hình lăng trụ đứng có chiều cao $20\,{\rm{cm}}$, đáy là một tam giác vuông có các cạnh góc vuông bằng $8\,{\rm{cm}}$ và $10\,{\rm{cm}}$.
-
A
\(800\,c{m^3}\)
-
B
\(400\,c{m^3}\)
-
C
\(600\,c{m^3}\)
-
D
\(500\,c{m^3}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng công thức tính thể tích hình lăng trụ đứng \(V = S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao.
Vì đáy là tam giác vuông nên diện tích đáy \(S = \dfrac{{8.10}}{2} = 40\,cm\) .
Thể tích lăng trụ đứng là \(V = S.h = 40.20 = 800\,c{m^3}\) .
Cho một hình lăng trụ đứng có diện tích đáy là $S$ , chiều cao là $h$ . Hỏi công thức tính thể tích hình lăng trụ đứng là gì?
-
A
$S.h\;\;\;\;\;\;$
-
B
\(\dfrac{1}{2}S.h\)
-
C
$2S.h$
-
D
$3S.h$
Đáp án của giáo viên lời giải hay : A
Công thức tính thể tích hình lăng trụ đứng là: $V = S.h$
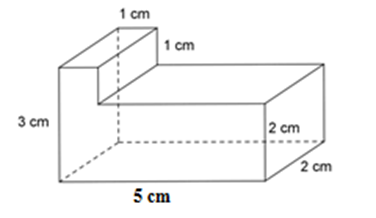
Tính thể tích của hình lăng trụ đứng sau:
-
A
\(16\;c{m^3}\)
-
B
\(20\;c{m^3}\)
-
C
\(26\;c{m^3}\)
-
D
\(22\;c{m^3}\)
Đáp án của giáo viên lời giải hay : D
- Chia hình lăng trụ đứng thành các hình hộp chữ nhật nhỏ hơn, sau đó tính thể tích từng hình hộp chữ nhật nhỏ.
- Tính được thể tích lăng trụ đứng bằng tổng thể tích các hình hộp chữ nhật nhỏ
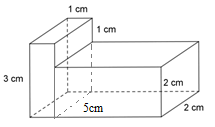
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là
\(3cm,\;\;1cm,\;\;2cm;\) hình hộp chữ nhật thứ hai có kích thước là \(2cm,\;\;4cm,\;\;2cm.\)
Thể tích hình hộp chữ nhật thứ nhất là: \({V_1} = 3.1.2 = 6\;c{m^3}\)
Thể tích hình hộp chữ nhật thứ hai là: \({V_2} = 2.4.2 = 16\;c{m^3}\)
Thể tích hình lăng trụ đứng là: \(V = {V_1} + {V_2} = 6 + 16 = 22\;c{m^3}\)
Một lăng trụ đứng có đáy là hình chữ nhật có các kích thức $3$ cm, $8$ cm. Chiều cao của hình lăng trụ đứng là $2$cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng.
-
A
\(48\;c{m^2},\;46\;c{m^3}\)
-
B
\(48\;c{m^2},\;44\;c{m^3}\)
-
C
\(46\;c{m^2},\;48\;c{m^3}\)
-
D
\(44\;c{m^2},\;48\;c{m^3}\)
Đáp án của giáo viên lời giải hay : D
- Áp dụng công thức tính diện tích xung quanh hình lăng trụ đứng và thể tích hình lăng trụ đứng để giải bài toán: \({S_{xq}} = 2\left( {a + b} \right)c,\;\;V = abc.\)

Diện tích xung quanh \({S_{xq}} = 2.(8 + 3).2 = 44\;c{m^2}\)
Thể tích của hình lăng trụ đứng là:\(V = 8.3.2 = 48\;c{m^3}\)
