Cho hình vẽ sau:
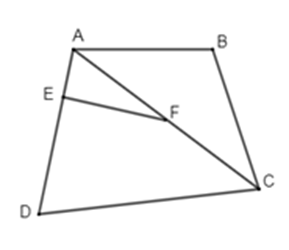
Em hãy chọn câu đúng nhất trong các câu sau:
-
A
\(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị
-
B
$\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía
-
C
\(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong
-
D
\(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị
Đáp án của giáo viên lời giải hay : A
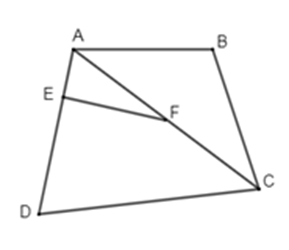
- \(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị (đúng, chọn A)
- $\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong) loại B
- \(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong (sai, vì đó là hai góc đồng vị) loại C
- \(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị (sai, vì đó là hai góc so le trong) loại D
Cho hình vẽ sau:
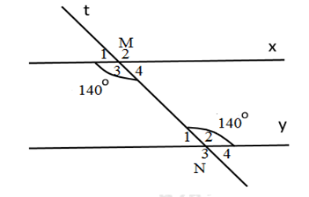
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
-
A
\({115^0}\)
-
B
\({55^0}\)
-
C
\({180^0}\)
-
D
\({145^0}\)
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất: Tổng hai góc kề bù bằng \({180^0}\).
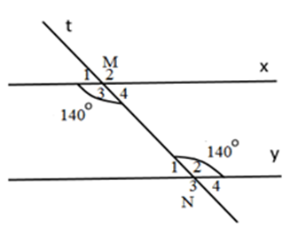
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{M_4}} = {180^0} - \widehat {{M_3}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_4}} + \,\widehat {{N_2}} = {40^0} + {140^0} = {180^0}\end{array}\)
Ta có: \(\widehat {{N_2}} + \widehat {{N_1}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{N_1}} = {180^0} - \widehat {{N_2}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_3}} + \widehat {{N_1}} = {140^0} + {40^0} = {180^0}\end{array}\)
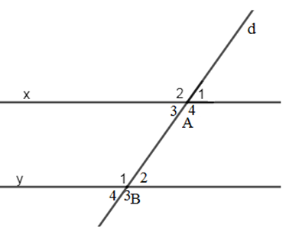
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
-
A
\({115^0}\)
-
B
\({55^0}\)
-
C
\({135^0}\)
-
D
\({145^0}\)
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau.
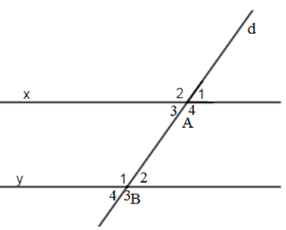
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1
cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\)nên \( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
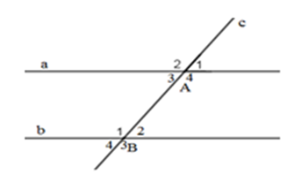
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
-
A
\(\widehat {{A_4}} = \widehat {{B_1}} = {150^0}\)
-
B
\(\widehat {{A_4}} = \widehat {{B_1}} = {120^0}\)
-
C
\(\widehat {{A_4}} = {120^o};\widehat {{B_1}} = {150^0}\) \(\)
-
D
\(\widehat {{A_4}} = \widehat {{B_1}} = {100^0}\)
Đáp án của giáo viên lời giải hay : A
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+) Hai góc so le trong còn lại bằng nhau.
+) Hai góc đồng vị bằng nhau.
Cặp góc so le trong còn lại là: \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\).
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {30^0} = {150^0}\\ \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {150^0}\end{array}\)
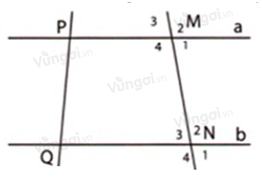
Trong hình dưới đây cho biết \(\widehat {{M_4}} = \widehat {{N_2}} = {100^0}\). Tính các góc tại đỉnh \(M,N.\)
-
A
\(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_1}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\)
-
B
\(\widehat {{M_1}} = \widehat {{N_1}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0};\widehat {{M_3}} = \widehat {{N_3}} = {60^0}\)
-
C
\(\widehat {{M_1}} = \widehat {{M_3}} = {80^0};\widehat {{N_1}} = \widehat {{N_3}} = {70^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\)
-
D
\(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_4}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_1}} = {100^0}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng:
+ Hai góc đối đỉnh thì bằng nhau
+ Tổng hai góc kề bù bằng \({180^0}\)
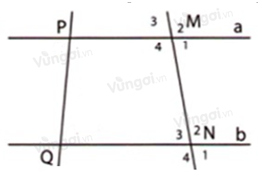
+ Tại \(M\):
Vì \(\widehat {{M_2}};\widehat {{M_4}}\) là hai góc đối đỉnh nên \(\widehat {{M_2}} = \widehat {{M_4}} = {100^0}\) (tính chất hai góc đối đỉnh)
Ta có: \(\widehat {{M_4}};\widehat {{M_1}}\) là hai góc kề bù nên \(\widehat {{M_4}} + \widehat {{M_1}} = {180^0}\) \( \Rightarrow \widehat {{M_1}} = {180^0} - \widehat {{M_4}} = {180^0} - {100^0} = {80^0}\)
Vì \(\widehat {{M_3}};\widehat {{M_1}}\) là hai góc đối đỉnh nên \(\widehat {{M_3}} = \widehat {{M_1}} = {80^0}\) (tính chất hai góc đối đỉnh)
+ Tại \(N\):
Vì \(\widehat {{N_2}};\widehat {{N_4}}\) là hai góc đối đỉnh nên \(\widehat {{N_4}} = \widehat {{N_2}} = {100^0}\) (tính chất hai góc đối đỉnh)
Ta có: \(\widehat {{N_2}};\widehat {{N_3}}\) là hai góc kề bù nên \(\widehat {{N_2}} + \widehat {{N_3}} = {180^0}\) \( \Rightarrow \widehat {{N_3}} = {180^0} - \widehat {{N_2}} = {180^0} - {100^0} = {80^0}\)
Vì \(\widehat {{N_3}};\widehat {{N_1}}\) là hai góc đối đỉnh nên \(\widehat {{N_3}} = \widehat {{N_1}} = {80^0}\) (tính chất hai góc đối đỉnh)
Vậy \(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_1}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\).
Cho hình vẽ sau:
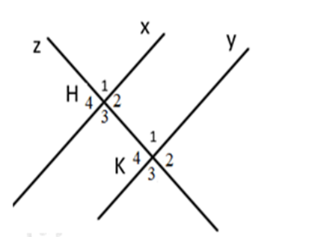
Chọn phát biểu đúng.
-
A
\(\widehat {\;{H_1}}\) và \(\widehat {\;{K_1}}\) là hai góc so le trong
-
B
\(\widehat {\;\;{H_4}}\) và \(\widehat {\;{K_4}}\) là hai góc đồng vị
-
C
\(\widehat {\;{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài
-
D
\(\widehat {\;{H_4}}\) và \(\widehat {\;{K_2}}\) là hai góc so le trong.
Đáp án của giáo viên lời giải hay : B
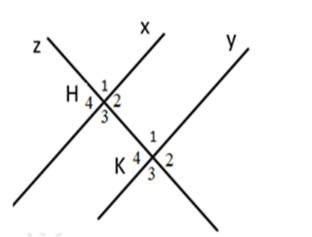
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
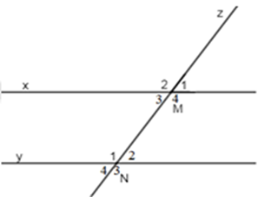
Chọn một cặp góc đồng vị trong hình vẽ sau:
-
A
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\)
-
B
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\)
-
C
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\)
-
D
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\)
Đáp án của giáo viên lời giải hay : D
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le ngoài) loại đáp án A.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le trong) loại đáp án B.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc trong cùng phía) loại đáp án C.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (đúng) chọn đáp án D.
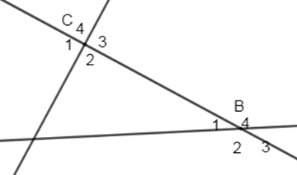
Chọn một cặp góc so le trong trong hình vẽ sau:
-
A
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\)
-
B
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\)
-
C
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\)
-
D
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\)
Đáp án của giáo viên lời giải hay : A
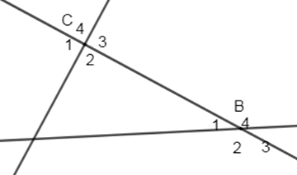
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (đúng) chọn A
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại B
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại C
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc trong cùng phía), loại D.
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
-
A
Hai góc trong cùng phía bằng nhau
-
B
Hai góc đồng vị bằng nhau
-
C
Hai góc so le trong còn lại có tổng bằng \({120^0}\)
-
D
Tất cả các đáp án trên đều đúng
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất: Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
+) Hai góc so le trong còn lại bằng nhau.
+) Hai góc đồng vị bằng nhau.
Nếu đường thẳng $c$ cắt hai đường thẳng $a,b$ và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: hai góc đồng vị bằng nhau
Cho hình vẽ sau:
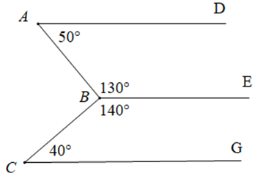
Chọn câu đúng.
-
A
\(AD//BE\)
-
B
\(BE//CG\)
-
C
Cả A, B đều sai
-
D
Cả A, B đều đúng.
Đáp án của giáo viên lời giải hay : D
Áp dụng tiên đề Ơ-clit, tính chất hai đường thẳng song song.
Vì \(\widehat A + \widehat {ABE} = 50^\circ + 130^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên $AD//BE.$
Vì \(\widehat {CBE} + \widehat C = 140^\circ + 40^\circ = 180^\circ \) mà hai góc ở vị trí trong cùng phía nên \(BE//CG.\)
Vậy cả A, B đều đúng.
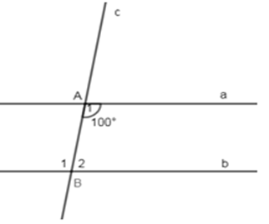
Cho hình vẽ sau, biết \(a//b\) và \(\widehat {{A_1}} = {100^0}\). Tính $\widehat {{B_1}},\widehat {{B_2}}$.
-
A
\(\widehat {{B_1}} = \widehat {{B_2}} = {100^0}\)
-
B
\(\widehat {{B_1}} = {100^0},\,\,\widehat {{B_2}} = {80^0}\)
-
C
\(\widehat {{B_1}} = {80^0},\,\,\widehat {{B_2}} = {100^0}\)
-
D
\(\widehat {{B_1}} = {100^0},\,\,\widehat {{B_2}} = {90^0}\)
Đáp án của giáo viên lời giải hay : B
Vì \(a//b\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\, = {100^0}\) (hai góc so le trong)
Lại có: \(\widehat {{A_1}} + \widehat {{B_2}} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {{B_2}} = {180^0} - \widehat {{B_1}} = {180^0} - {100^0} = {80^0}.\)
Cho hình vẽ sau:
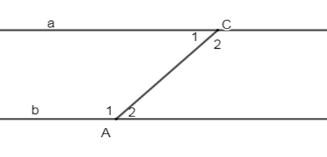
Biết \(a\,//\,b,\,\widehat {{A_1}} - \widehat {{C_1}} = {40^0}\). Tính \(\widehat {{A_2}},\,\widehat {{C_2}}\).
-
A
\(\widehat {{A_2}} = 80^\circ ;\,\widehat {{C_2}} = 110^\circ \)
-
B
\(\widehat {{A_2}} = 110^\circ ;\,\widehat {{C_2}} = 70^\circ \)
-
C
\(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 110^\circ \)
-
D
\(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 70^\circ \)
Đáp án của giáo viên lời giải hay : C
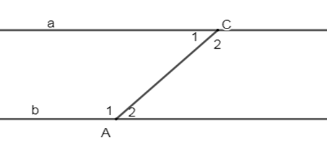
Vì \(a\,//\,b\left( {gt} \right) \Rightarrow \widehat {{A_1}} + \widehat {{C_1}} = {180^0}\) (2 góc trong cùng phía bù nhau)
Mà lại có:
\(\begin{array}{l}\widehat {{A_1}} - \widehat {{C_1}} = {40^0}\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \left( {{{180}^0} + {{40}^0}} \right):2 = {110^0}\\ \Rightarrow \widehat {{C_1}} = {110^0} - {40^0} = {70^0}\end{array}\)
Vì $a\,//\,b\left( {gt} \right) \Rightarrow \left\{ \begin{array}{l}\widehat {{A_1}} = \widehat {{C_2}} = {110^0}\\\widehat {{C_1}} = \widehat {{A_2}} = {70^0}\end{array} \right.$(2 góc so le trong)
Vậy \(\widehat {{A_2}} = 70^\circ ;\,\widehat {{C_2}} = 110^\circ .\)
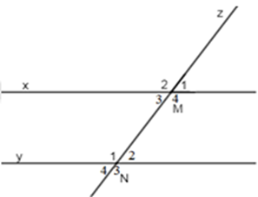
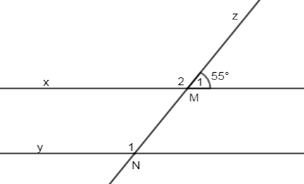
Cho hình vẽ sau, biết \(x//y\) và \(\widehat {{M_1}} = {55^0}\). Tính \(\widehat {{N_1}}\).
-
A
\({55^0}\)
-
B
\({35^0}\)
-
C
\({60^0}\)
-
D
\({125^0}\)
Đáp án của giáo viên lời giải hay : D
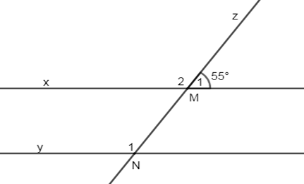
Ta có: \(\widehat {{M_1}} + \widehat {{M_2}} = {180^0} \Rightarrow \widehat {{M_2}} = {180^0} - {55^0} = {125^0}\) (kề bù)
Vì \(x//y\left( {gt} \right) \Rightarrow \widehat {{M_2}} = \widehat {{N_1}} = {125^0}\) (2 góc đồng vị)
Cho hình vẽ:
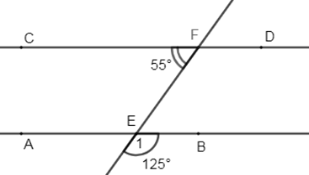
Biết \(\widehat {CF{\rm{E}}} = {55^0},\,\widehat {{E_1}} = {125^0}\) . Khi đó:
-
A
\(\widehat {AEF} = 125^\circ \)
-
B
\(AB//C{\rm{D}}\)
-
C
Cả A, B đều đúng
-
D
Cả A, B đều sai
Đáp án của giáo viên lời giải hay : C
Áp dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng $c$ cắt hai đường thẳng $a$ và $b,$ trong các góc tạo thành có $1$ cặp góc so le trong bằng nhau thì \(a//b\).
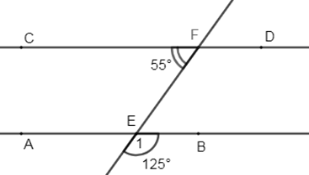
Vì \(\widehat {{E_1}}\) và \(\widehat {BEF}\) là hai góc kề bù (gt)
\( \Rightarrow \widehat {{E_1}} + \widehat {BEF} = {180^0} \)\(\Rightarrow \widehat {BEF} = {180^0} - \widehat {{E_1}} \)\(= {180^0} - {125^0} = {55^0} \)\(\Rightarrow \widehat {BEF} = \widehat {CFE} = {55^0}\)
Mà \(\widehat {BEF}\) và \(\widehat {CFE}\) là hai góc so le trong nên suy ra \(AB//C{\rm{D}}\) (dấu hiệu nhận biết hai đường thẳng song song)
Lại có \(\widehat {{E_1}}=\widehat {{AEF}}\) (hai góc đối đỉnh) nên \(\widehat {{AEF}}=125^0\)
Vậy cả A, B đều đúng.
Cho hình vẽ dưới đây, biết \(a//b\). Tính \(x;y.\)
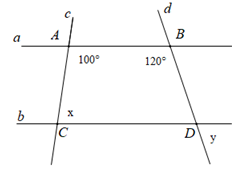
-
A
\(x = 80^\circ ;y = 80^\circ .\)
-
B
\(x = 60^\circ ;y = 80^\circ .\)
-
C
\(x = 80^\circ ;y = 60^\circ .\)
-
D
\(x = 60^\circ ;y = 60^\circ .\)
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất hai đường thẳng song song để tính \(x.\)
Áp dụng tính chất hai góc đối đỉnh để tính \(y.\)
Vì \(a//b\) nên \(\widehat {BAC} + \widehat {ACD} = 180^\circ \) (hai góc trong cùng phía bù nhau)
Suy ra \(100^\circ + x = 180^\circ \Rightarrow x = 80^\circ \)
Tương tự ta có \(\widehat {ABD} + \widehat {CDB} = 180^\circ \Rightarrow \widehat {CDB} = 60^\circ \)
Suy ra \(y = \widehat {CDB} = 60^\circ \) (hai góc đổi đỉnh)
Vậy \(x = 80^\circ ;y = 60^\circ .\)
Cho hình vẽ dưới đây :
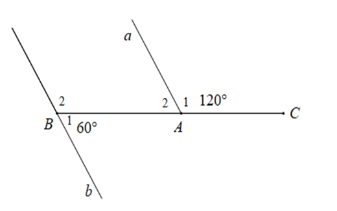
Chọn câu sai.
-
A
\(a \bot b\)
-
B
\(\widehat {{A_2}} = 60^\circ \)
-
C
\(\widehat {{B_2}} = 120^\circ \)
-
D
\(a//b\)
Đáp án của giáo viên lời giải hay : A
+ Áp dụng tính chất hai góc kề bù để tính \(\widehat {{A_2}};\,\widehat {{B_2}}.\)
+ Sử dụng dấu hiệu nhận biết để suy ra hai đường thẳng song song
Vì \(\widehat {{A_1}};\widehat {{A_2}}\) là hai góc kề bù nên \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) \( \Rightarrow 120^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 60^\circ \)
Tương tự vì \(\widehat {{B_1}};\widehat {{B_2}}\) là hai góc kề bù nên \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) \( \Rightarrow 60^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 120^\circ \)
Nhận thấy \(\widehat {{A_2}} = \widehat {{B_2}} = 120^\circ \) mà hai góc ở vị trí đồng vị nên \(a//b.\)
Vậy A sai.
Chọn câu đúng nhất.
-
A
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc so le trong bằng nhau thì $a//b.$
-
B
Nếu hai đường thẳng $a,b$ cắt đường thẳng c tạo thành một cặp góc đồng vị bằng nhau thì $a//b.$
-
C
Hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp góc so le ngoài bằng nhau thì \(a//b.\)
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le trong bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc đồng vị bằng nhau thì hai đường thẳng song song.
+ Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành một cặp góc so le ngoài bằng nhau thì hai đường thẳng song song.
nên cả A, B, C đều đúng.
Chọn câu trả lời đúng trong các câu sau: Trong mặt phẳng,
-
A
Hai đường thẳng không có điểm chung thì song song với nhau.
-
B
Hai đoạn thẳng có điểm chung thì song song với nhau.
-
C
Hai đường thẳng có hai điểm chung thì song song với nhau.
-
D
Hai đường thẳng song song là hai đường thẳng không trùng nhau.
Đáp án của giáo viên lời giải hay : A
Hai đường thẳng song song (trong mặt phẳng) là hai đường thẳng không có điểm chung.
Chọn câu đúng.
-
A
Qua điểm A nằm ngoài đường thẳng m, có vô số đường thẳng song song với m.
-
B
Qua điểm A nằm ngoài đường thẳng m, có duy nhất một đường thẳng song song với m.
-
C
Qua điểm A nằm ngoài đường thẳng d, có hai đường thẳng phân biệt cùng song song với d.
-
D
Nếu hai đường thẳng AB và AC cùng song song với đường thẳng d thì hai đường thẳng AB và AC song song với nhau.
Đáp án của giáo viên lời giải hay : B
Sử dụng tiên đề Ơ-clit về hai đường thẳng song song
Tiên đề Ơ-clit: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó.”
