Cho ba điểm \(M;N;P\) thẳng hàng với \(P\) nằm giữa \(M\) và \(N.\) Chọn hình vẽ đúng.
-
A
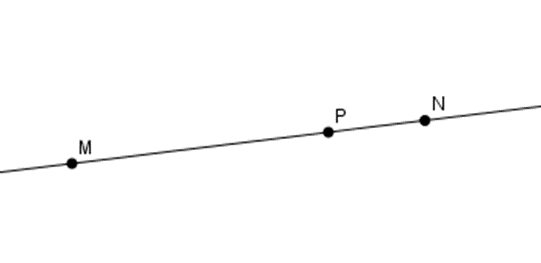
-
B
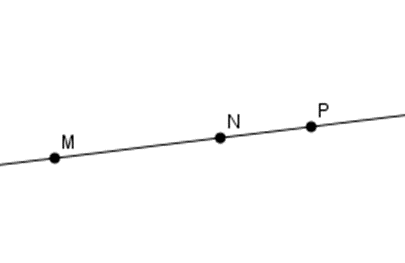
-
C
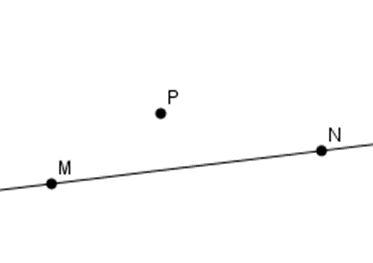
-
D
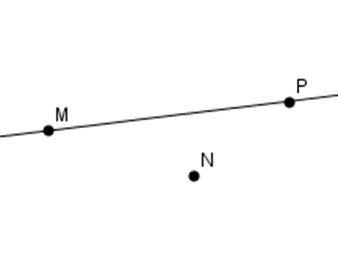
Đáp án của giáo viên lời giải hay : A
Xét từng đáp án:
- Kiểm tra xem ba điểm \(M,N,P\) có thẳng hàng hay không.
- Kiểm tra điểm \(P\) nằm giữa hai điểm \(M,N\)
Đáp án A: Ta thấy ba điểm \(M,N,P\) thẳng hàng và điểm \(P\) nằm giữa hai điểm \(M,N\) nên A đúng.
Đáp án B: Ta thấy ba điểm \(M,N,P\) thẳng hàng và điểm \(P\) không nằm giữa hai điểm \(M,N\) nên B sai.
Đáp án C: Ta thấy ba điểm \(M,N,P\) không thẳng hàng nên C sai.
Đáp án D: Ta thấy ba điểm \(M,N,P\) không thẳng hàng nên D sai.
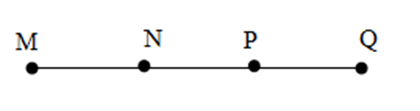
Cho bốn điểm $M;N;P;Q$ cùng nằm trên một đường thẳng và hai điểm $M;N$ nằm cùng phía đối với điểm $Q$ còn hai điểm $N,P$ nằm khác phía đối với điểm $Q.$ Một hình vẽ đúng là:
-
A
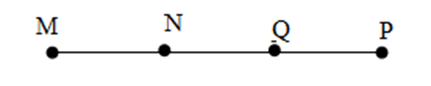
-
B
-
C
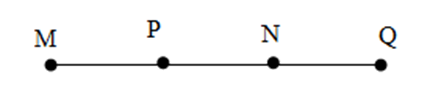
-
D
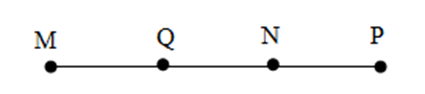
Đáp án của giáo viên lời giải hay : A
Quan sát hình vẽ ở các đáp án, đối chiếu với yêu cầu bài cho rồi kết luận
Đáp án A: Hai điểm \(M,N\) nằm cùng phía so với \(Q\) và hai điểm \(N,P\) khác phía so với \(Q\) nên thỏa mãn, chọn A.
Đáp án B: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại B.
Đáp án C: Hai điểm \(N,P\) cùng phía so với \(Q\) nên không thỏa mãn, loại C.
Đáp án D: Hai điểm \(M,N\) nằm khác phía so với \(Q\) nên không thỏa mãn, loại D.
Cho hình vẽ sau:
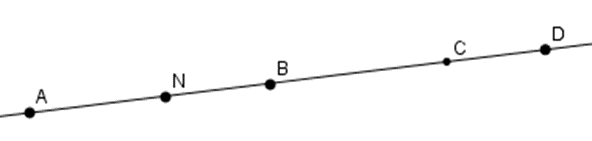
Kể tên các điểm nằm giữa \(A\) và \(D.\)
-
A
\(N,B,C\)
-
B
\(B,C,D\)
-
C
\(N\)
-
D
\(B,C\)
Đáp án của giáo viên lời giải hay : A
Quan sát hĩnh vẽ và tìm các điểm nằm giữa \(A\) và \(D\)
Các điểm nằm giữa \(A\) và \(D\) là \(N,B,C\)
Có bao nhiêu điểm nằm giữa \(N\) và \(D?\)
-
A
\(3\)
-
B
\(1\)
-
C
\(2\)
-
D
\(0\)
Đáp án của giáo viên lời giải hay : C
Tìm các điểm nằm giữa hai điểm \(N,D\) rồi kết luận.
Các điểm nằm giữa \(N\) và \(D\) là \(B,C\)
Vậy có \(2\) điểm cần tìm.
Số cặp điểm nằm cùng phía với điểm \(A\) là:
-
A
\(9\)
-
B
\(18\)
-
C
\(12\)
-
D
\(6\)
Đáp án của giáo viên lời giải hay : D
Liệt kê tất cả các cặp điểm nằm cùng phía với điểm \(A\)
Các cặp điểm nằm cùng phía so với điểm \(A\) là:
\(\left( {N,B} \right),\left( {N,C} \right),\left( {N,D} \right),\) \(\left( {B,C} \right),\left( {B,D} \right),\left( {C,D} \right)\)
Vậy có \(6\) cặp điểm thỏa mãn bài toán.
Trên hình vẽ, điểm \(B\) nằm giữa bao nhiêu cặp điểm?
-
A
\(10\)
-
B
\(8\)
-
C
\(4\)
-
D
\(6\)
Đáp án của giáo viên lời giải hay : C
Liệt kê các cặp điểm thỏa mãn điểm \(B\) nằm giữa.
Điểm \(B\) nằm giữa các cặp điểm là:
\(\left( {N,C} \right),\left( {A,D} \right),\left( {A,C} \right),\left( {N,D} \right)\)
Vậy có \(4\) cặp điểm thỏa mãn bài toán.
Cho hình vẽ sau:

Trên hình vẽ, điểm \(B\) và \(D\) nằm khác phía với mấy điểm?
-
A
\(0\)
-
B
\(3\)
-
C
\(4\)
-
D
\(1\)
Đáp án của giáo viên lời giải hay : D
Tìm số điểm nằm giữa hai điểm \(B,D\) trong hình vẽ rồi suy ra kết luận.
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,C\) nằm khác phía so với \(B\).
Trong hình vẽ chỉ có điểm \(C\) nằm giữa hai điểm \(B\) và \(D\) nên chỉ có \(1\) điểm thỏa mãn yêu cầu bài toán.
Trên hình vẽ, điểm \(A\) và \(B\) nằm cùng phía với các điểm nào?
-
A
điểm \(C\)
-
B
điểm \(D\)
-
C
điểm \(B\)
-
D
Cả điểm \(C\) và điểm \(D\)
Đáp án của giáo viên lời giải hay : D
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,B\) nằm cùng phía so với \(C\) và \(B,C\) nằm cùng phía so với \(A\).
Trên hình vẽ, hai điểm \(A,B\) nằm cùng phía so với các điểm \(C,D\).
Điểm \(A\) và \(C\) nằm cùng phía với điểm nào?
-
A
điểm \(D\)
-
B
điểm \(B\)
-
C
điểm \(A\)
-
D
Cả điểm \(D\) và điểm \(B\)
Đáp án của giáo viên lời giải hay : A
Sử dụng kiến thức: Nếu điểm \(B\) nằm giữa hai điểm \(A,C\) thì ta nói hai điểm \(A,B\) nằm cùng phía so với \(C\) và \(B,C\) nằm cùng phía so với \(A\).
Trên hình vẽ, hai điểm \(A,C\) nằm cùng phía so với điểm \(D\) và nằm khác phía so với điểm \(B\).
Chọn câu sai.
-
A
Điểm \(B\) nằm giữa \(A\) và \(C.\)
-
B
Điểm \(B\) nằm giữa \(A\) và \(D.\)
-
C
Điểm \(C\) nằm giữa \(A\) và \(B.\)
-
D
Điểm \(C\) nằm giữa \(D\) và \(A.\)
Đáp án của giáo viên lời giải hay : C
Quan sát hình vẽ và nhận xét tính đúng sai của từng đáp án.
Chú ý: Trong ba điểm thẳng hàng chỉ có \(1\) điểm nằm giữa hai điểm còn lại.
Đáp án A: Điểm \(B\) nằm giữa \(A\) và \(C\) nên A đúng và C sai.
Đáp án B: Điểm \(B\) nằm giữa \(A\) và \(D\) nên B đúng.
Điểm \(C\) nằm giữa \(D\) và \(A\) nên D đúng.
Kể tên các tia trong hình vẽ sau
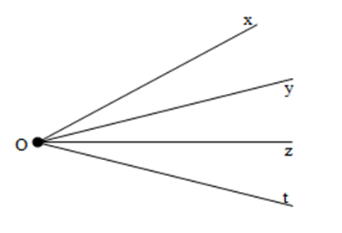
-
A
\(Ox\)
-
B
\(Ox,Oy,Oz,Ot\)
-
C
\(Ox,Oy,Oz\)
-
D
\(xO,yO,zO,tO\)
Đáp án của giáo viên lời giải hay : B
Sử dụng định nghĩa tia:
- Hình gồm điểm $O$ và một phần đường thẳng bị chia ra bởi điểm $O$ được gọi là một tia gốc $O,$ còn gọi là một nửa đường thẳng gốc $O.$
Các tia trong hình vẽ là: \(Ox,Oy,Oz,Ot\)
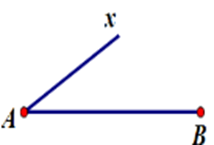
Cho $AB$ và $Ax$ là hai tia trùng nhau. Hãy chọn hình vẽ đúng.
-
A
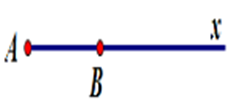
-
B
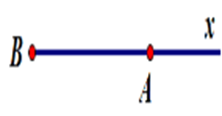
-
C
-
D
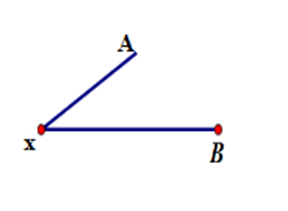
Đáp án của giáo viên lời giải hay : A
Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.
Xét các tia trong hình vẽ ở mỗi đáp án xem chúng trùng nhau hay không và kết luận.
Hình A: Hai tia $AB$ và $Ax$ chung gốc $A\;$
Hai tia $AB$ và $Ax$ cùng nằm trên nửa đường thẳng chứa tia $Ax$
Nên hai tia $AB$ và $Ax$ là hai tia trùng nhau.
Hình B: Hai tia \(AB,Ax\) đối nhau nên loại.
Hình C: Hai tia \(AB,Ax\) chỉ có chung mỗi điểm \(A\) nên không trùng nhau.
Hình D: Hình vẽ tia \(Ax\) chưa đúng.
Cho tia $AB,$ lấy $M$ thuộc tia $AB.$ Khẳng định nào sau đây đúng?
-
A
\(M\) và \(A\) nằm cùng phía so với \(B\)
-
B
\(M\) và \(B\) nằm cùng phía so với \(A\)
-
C
\(A\) và \(B\) nằm cùng phía so với \(M\)
-
D
\(M\) nằm giữa \(A\) và \(B\)
Đáp án của giáo viên lời giải hay : B
Vẽ hình theo hai trường hợp $M$ có thể nằm giữa $A$ và $B$ hoặc $B$ nằm giữa $A$ và $M$ rồi loại đáp án.
Vì $M$ thuộc tia $AB$ nên $M$ có thể nằm giữa $A$ và $B$ hoặc $B$ nằm giữa $A$ và $M$
Ta có hình vẽ:
Th1:

Từ hình vẽ ta thấy đáp án C sai nên loại C.
Th2:
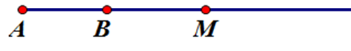
Từ hình vẽ ta thấy đáp án A, D sai nên loại A, D.
Cả hai hình vẽ đều có \(M\) và \(B\) nằm cùng phía so với \(A\) nên B đúng.
Cho hai tia đối nhau $MA$ và $MB,$ $X$ là $1$ điểm thuộc tia $MA.$ Trong $3$ điểm $X,{\rm{ }}M,{\rm{ }}B$ điểm nào nằm giữa hai điểm còn lại?
-
A
chưa kết luận được
-
B
\(X\)
-
C
\(B\)
-
D
\(M\)
Đáp án của giáo viên lời giải hay : D
Có thể sử dụng phương pháp sau:
Nếu $Ax$ và $Ay$ là hai tia đối nhau, mà điểm $M$ thuộc tia $Ax,$ điểm $N$ thuộc tia $Ay$ thì điểm $A$ nằm giữa hai điểm $M$ và $N$
Theo đề bài ta có hình vẽ:

Vì hai tia \(MA,MB\) đối nhau và \(X\) thuộc tia \(MA\) và \(B\) thuộc tia \(MB\) nên điểm \(M\) nằm giữa hai điểm \(B,X\)
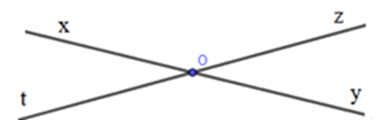
Trong hình vẽ sau, có bao nhiêu tia
-
A
\(2\)
-
B
\(0\)
-
C
\(4\)
-
D
\(1\)
Đáp án của giáo viên lời giải hay : C
Liệt kê các tia có trong hình vẽ với chú ý điểm \(O\) thuộc hai đường thẳng \(xy,zt\)
Có các tia là $Ox,Oy,Oz,Ot.$
Vậy có $4$ tia.
Vẽ hình theo cách diễn đạt sau:
+ Vẽ hai tia phân biệt $Ox$ và \(Oy\) chung gốc nhưng không đối nhau, không trùng nhau
+ Vẽ đường thẳng \(aa'\) cắt hai tia \(Ox;\,Oy\) theo thứ tự tại \(A\) và \(B\)(khác \(O\))
+ Vẽ điểm \(C\) nằm giữa hai điểm \(A;B\) sau đó vẽ tia \(Oz\) đi qua \(C\)
Có bao nhiêu tia phân biệt trên hình vẽ thu được.
-
A
\(6\)
-
B
\(12\)
-
C
\(9\)
-
D
\(15\)
Đáp án của giáo viên lời giải hay : B
Vẽ hình, liệt kê các tia phân biệt dựa vào kiến thức:
Hai tia không trùng nhau còn được gọi là hai tia phân biệt.
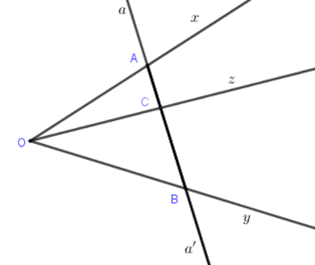
Các tia phân biệt trong hình là:
\(Ox,Oy,Oz,Aa,Aa',Ca,Ca',Ba,Ba',Ax,By,Cz\)
Có tất cả \(12\) tia phân biệt.
Cho hình vẽ sau
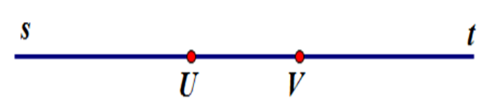
Một cặp tia đối nhau là:
-
A
\(Ut,UV\)
-
B
\(Us,Vt\)
-
C
\(Vs,Vt\)
-
D
\(Vs,Ut\)
Đáp án của giáo viên lời giải hay : C
Định nghĩa hai tia đối nhau:
Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.
Các cặp tia đối nhau có trong hình là:
$Us,Uv$ hoặc \(Us,Ut;\) \(Vt,VU\) hoặc \(Vt,Vs\)
Đối chiếu với các đáp án ta thấy đáp án C đúng.
Kể tên các tia trùng nhau trên hình vẽ
-
A
Tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)
-
B
Tia \(Us\) và tia \(Vs\); tia \(VU\) và tia \(Vs\)
-
C
Tia \(Ut\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)
-
D
Tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Us\)
Đáp án của giáo viên lời giải hay : A
Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.
Các cặp tia trùng nhau trong hình là: tia \(UV\) và tia \(Ut\); tia \(VU\) và tia \(Vs\)
Vẽ đường thẳng $mn.$ Lấy điểm $O$ trên đường thẳng $mn,$ trên tia $Om$ lấy điểm $A,$ trên tia $On$ lấy điểm $B.$
Một cặp tia đối nhau gốc $O$ là:
-
A
\(OB,AO\)
-
B
\(mO,nO\)
-
C
\(OA,Om\)
-
D
\(OA,On\)
Đáp án của giáo viên lời giải hay : D
Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Các cặp tia đối nhau gốc \(O\) là: \(OA,OB\) (hoặc \(OA,On\) hoặc \(OB,Om\) hoặc \(Om,On\))
Một cặp tia đối nhau gốc $B$ là:
-
A
\(Bn,BA\)
-
B
\(BO,BA\)
-
C
\(Bm,BA\)
-
D
\(OB,Bn\)
Đáp án của giáo viên lời giải hay : A
Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.

Các cặp tia đối nhau gốc \(B\) là: \(Bn,BO\) hoặc \(Bn,BA\) hoặc \(Bn,Bm\)
Có bao nhiêu cặp tia trùng nhau gốc \(O?\)
-
A
\(2\)
-
B
\(4\)
-
C
\(3\)
-
D
\(0\)
Đáp án của giáo viên lời giải hay : A
Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc

Các cặp tia trùng nhau gốc \(O\) là:
\(OA,Om\) và \(OB,On\)
Vậy có hai cặp tia trùng nhau gốc \(O\)
Trong ba điểm \(O;A;B\) thì điểm nào nằm giữa hai điểm còn lại?
-
A
\(A\)
-
B
\(O\)
-
C
\(B\)
-
D
chưa kết luận được
Đáp án của giáo viên lời giải hay : B
Sử dụng chú ý sau:
Nếu $Ax$ và $Ay$ là hai tia đối nhau, mà điểm $M$ thuộc tia $Ax,$ điểm $N$ thuộc tia $Ay$ thì điểm $A$ nằm giữa hai điểm $M$ và $N$

Vì điểm \(O\) nằm trên đường thẳng \(mn\) nên hai tia \(Om,On\) đối nhau.
Mà điểm \(A\) thuộc tia \(Om\) và điểm \(B\) thuộc tia \(On\) nên điểm \(O\) nằm giữa hai điểm \(A,B\)
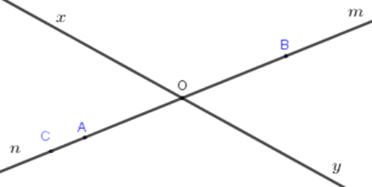
Vẽ hai đường thẳng \(xy\) và \(mn\) cắt nhau tại \(O.\)
Kể tên các cặp tia đối nhau.
-
A
Không có cặp tia đối nhau
-
B
Cặp tia \(Ox,On\) và cặp tia \(Om,Oy\)
-
C
Cặp tia \(Ox,Oy\) và cặp tia \(Om,On\)
-
D
Cặp tia \(Ox,Om\) và cặp tia \(Oy,On\)
Đáp án của giáo viên lời giải hay : C
Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.
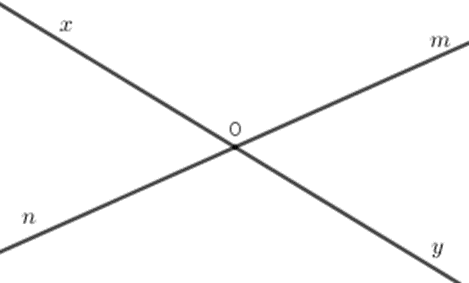
Các cặp tia đối nhau là:\(Ox,Oy\) và \(Om,On\)
Trên tia \(On\) lấy điểm \(A,\) trên tia \(Om\) lấy điểm \(B\). Kể tên các tia trùng nhau.
-
A
\(OA,On\) và \(OB,Om\) và \(Ox,Oy\)
-
B
\(OA,On\) và \(OB,Om\)
-
C
\(OA,On\) và \(Ox,Oy\)
-
D
\(OA,OB\) và \(OB,Om\)
Đáp án của giáo viên lời giải hay : B
Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc
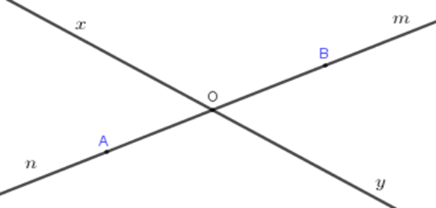
Các cặp tia trùng nhau là: \(OA,On\) và \(OB,Om\)
Trên tia \(On\) lấy điểm \(A,\) trên tia \(Om\) lấy điểm \(B\). Lấy điểm $C$ sao cho điểm \(O\) nằm giữa hai điểm \(B\) và \(C.\) Khi đó điểm \(C\) thuộc tia nào?
-
A
\(Ox,Oy\)
-
B
\(Oy,OA\)
-
C
\(Om,OA\)
-
D
\(On,OA\)
Đáp án của giáo viên lời giải hay : D
Nếu điểm \(O\) nằm giữa hai điểm\(A\) và \(B\) thì hai tia \(OA;OB\) đối nhau
Vì điểm \(O\) nằm giữa hai điểm \(B,C\) nên hai tia \(OB,OC\) đối nhau.
Nên \(C\) nằm trên tia đối của tia \(OB\) hay \(C\) nằm trên tia \(OA\) hoặc \(On\)
Cho hình vẽ sau

Tia nào trùng với tia $Ay$?
-
A
Tia $Ax$
-
B
Tia $OB,By$
-
C
Tia $BA$
-
D
Tia $AO,AB$
Đáp án của giáo viên lời giải hay : D
Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.
Có $2$ tia trùng với tia $Ay$ đó là tia $AO$ và tia $AB.$
Hai tia $Ax$ và $By$ có vị trí như thế nào với nhau
-
A
Đối nhau
-
B
Trùng nhau
-
C
Không đối nhau, không trùng nhau
-
D
Vừa đối nhau, vừa trùng nhau
Đáp án của giáo viên lời giải hay : C
Quan sát hình vẽ và nhận xét dựa vào gốc của hai tia \(Ax,By\)
Chú ý:
- Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc.
- Hai tia chung gốc và tạo thành một đường thẳng gọi là hai tia đối nhau.
Hai tia $Ax$ và $By$ không chung gốc và nằm về hai phía khác nhau nên chúng không trùng nhau cũng không đối nhau .
