Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
-
A
Điểm cách đều ba cạnh của \(\Delta ABC\).
-
B
Điểm cách đều ba đỉnh của \(\Delta ABC\).
-
C
Tâm đường tròn ngoại tiếp \(\Delta ABC\).
-
D
Đáp án B và C đúng
Đáp án của giáo viên lời giải hay : D
Tính chất đồng quy của 3 đường trung trực trong một tam giác.
Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
-
A
Tam giác vuông
-
B
Tam giác cân
-
C
Tam giác đều
-
D
Tam giác vuông cân
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất đường trung trực và đường trung tuyến của tam giác.
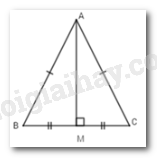
Giả sử \(\Delta ABC\) có $AM$ là trung tuyến đồng thời là đường trung trực.
Ta sẽ chứng minh \(\Delta ABC\) là tam giác cân.
Thật vậy, vì $AM$ là trung tuyến của \(\Delta ABC\) (gt) \( \Rightarrow BM = MC\) (tính chất trung tuyến)
Vì $AM$ là trung trực của $BC$ $ \Rightarrow AM \bot BC$
Xét hai tam giác vuông \({\Delta}ABM\) và \({\Delta}ACM\) có:
\(BM = CM\left( {cmt} \right)\)
$AM$ chung
\( \Rightarrow \Delta ABM = \Delta ACM\) (2 cạnh góc vuông)
\( \Rightarrow AB = AC\) (2 cạnh tương ứng) \( \Rightarrow \Delta ABC\) cân tại $A.$
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
-
A
\({30^0}\)
-
B
\({45^0}\)
-
C
\({60^0}\)
-
D
\({40^0}\).
Đáp án của giáo viên lời giải hay : A
Áp dụng tính chất đường trung trực của đoạn thẳng, tính chất tam giác cân.
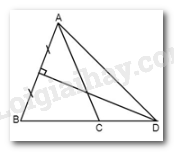
Vì \(\Delta ABC\) cân tại A (gt) \( \Rightarrow \widehat B = \widehat C = \left( {{{180}^0} - \widehat A} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Vì $D$ thuộc đường trung trực của $AB$ nên
\( \Rightarrow AD = BD\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ABD\) cân tại $D$ (dấu hiệu nhận biết tam giác cân)
$ \Rightarrow \widehat {DAC} + \widehat {CAB} = \widehat {DAB} = \widehat B = {70^0} \Rightarrow \widehat {DAC} = {70^0} - \widehat {CAB} = {70^0} - {40^0} = {30^0}.$
Cho tam giác \(ABC\) trong đó \(\widehat A = 100^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\) . Tính \(\widehat {EAF}.\)
-
A
\(20^\circ \)
-
B
\(30^\circ \)
-
C
\(40^\circ \)
-
D
\(50^\circ \)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng tính chất đường trung trực
+ Sử dụng tính chất tam giác cân để tính góc \(EAF.\)
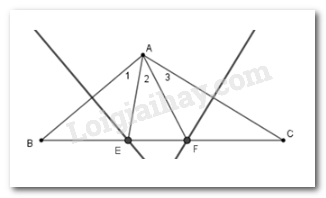
Vì E nằm trên đường trung trực của AB nên \(EA = EB\) ( tính chất) nên \(\widehat {{A_1}} = \widehat B\)
Vì F nằm trên đường trung trực của AC nên \(FA = FC\) ( tính chất) nên \(\widehat {{A_3}} = \widehat C\).
Do đó \(\widehat {{A_1}} + \widehat {{A_3}} = \widehat B + \widehat C = 180^\circ - 100^\circ = 80^\circ \)
\(\Rightarrow \widehat {{A_2}} = 100^\circ - 80^\circ = 20^\circ .\)
Cho \(\Delta ABC\) nhọn, đường cao $AH.$ Lấy điểm $D$ sao cho $AB$ là trung trực của $HD.$ Lấy điểm $E$ sao cho $AC$ là trung trực của $HE.$ Gọi $M$ là giao điểm của $DE$ với $AB,N$ là giao điểm của $DE$ với $AC.$ Chọn câu đúng.
-
A
\(\Delta ADE\) là tam giác cân
-
B
$HA$ là tia phân giác của \(\widehat {MHN}\).
-
C
A, B đều đúng
-
D
A, B đều sai
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất đường trung trực của đoạn thẳng và tính chất hai tam giác bằng nhau..
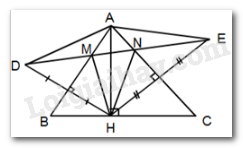
Vì $AB$ là đường trung trực của $HD$ (gt) \( \Rightarrow AD = AH\) (tính chất trung trực của đoạn thẳng)
Vì $AC$ là đường trung trực của $HE$ (gt) \( \Rightarrow AH = AE\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow AD = AE \Rightarrow \Delta ADE\) cân tại $A.$ Nên A đúng.
+) $M$ nằm trên đường trung trực của $HD$ nên $MD = MH$ (tính chất đường trung trực của đoạn thẳng)
Xét \(\Delta AMD\) và \(\Delta AMH\) có:
\(\)$AM$ chung.
$AD = AH$ (cmt)
$MD = MH$ (cmt)
\( \Rightarrow \Delta AMD = \Delta AMH\left( {c - c - c} \right) \Rightarrow \widehat {MDA} = \widehat {MHA}\) (2 góc tương ứng)
Lại có, $N$ thuộc đường trung trực của $HE$ nên $NH = NE$ (tính chất đường trung trực của đoạn thẳng).
+) Xét \(\Delta AHN\) và \(\Delta AEN\) có:
$AN$ chung
$AH = AE$ (cmt)
$NH = NE$ (cmt)
\( \Rightarrow \Delta AHN = \Delta AEN\left( {c - c - c} \right)\)
\(\Rightarrow \widehat {NHA} = \widehat {NEA}\) (2 góc tương ứng)
Mà \(\Delta ADE\) cân tại $A$ (cmt) \( \Rightarrow \widehat {MDA} = \widehat {NEA} \Rightarrow \widehat {MHA} = \widehat {NHA}\) .
Vậy $HA$ là đường phân giác của \(\widehat {MHN}\) .
Cho \(\Delta ABC\) vuông tại $A,$ có \(\widehat C = {30^0}\), đường trung trực của $BC$ cắt $AC$ tại $M.$ Em hãy chọn câu đúng:
-
A
$BM$ là đường trung tuyến của \(\Delta ABC\)
-
B
\(BM = AB\).
-
C
$BM$ là phân giác của \(\widehat {ABC}\).
-
D
$BM$ là đường trung trực của \(\Delta ABC\).
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất tam giác cân, tính chất đường trung trực của đoạn thẳng, định lý tổng 3 góc trong tam giác
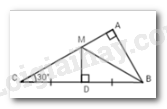
Vì $M$ thuộc đường trung trực của $BC$ \( \Rightarrow BM = MC\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta BMC\) cân tại $M$ (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat {MBC} = \widehat C = {30^0}\) (tính chất tam giác cân)
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ABC} + \widehat C = {180^0}\) (định lý tổng 3 góc trong tam giác)
\( \Rightarrow \widehat {ABC} = {180^0} - \widehat C - \widehat A = {180^0} - {30^0} - {90^0} = {60^0}\)
\( \Rightarrow \widehat {ABM} + \widehat {MBC} = \widehat {ABC} = {60^0} \Rightarrow \widehat {ABM} = {60^0} - \widehat {MBC} = {60^0} - {30^0} = {30^0}\)
\( \Rightarrow \widehat {ABM} = \widehat {MBC}\)
\(\Rightarrow \) $BM$ là phân giác của \(\widehat {ABC}\).
Cho tam giác $ABC$ vuông tại $A,$ kẻ đường cao $AH.$ Trên cạnh $AC$ lấy điểm $K$ sao cho $AK = AH.$ Kẻ \(KD \bot AC\left( {D \in BC} \right)\). Chọn câu đúng.
-
A
\(\Delta AHD = \Delta AKD\)
-
B
$AD$ là đường trung trực của đoạn thẳng $HK.$
-
C
\(AD\) là tia phân giác của góc \(HAK.\)
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông
+ Sử dụng tính chất hai tam giác bằng nhau để chứng minh \(AD\) là tia phân giác của góc \(HAK.\)
+ Sử dụng định lý về đường trung trực để chỉ ra $AD$ là đường trung trực của đoạn thẳng $HK.$
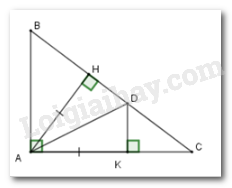
Xét tam giác vuông \(AHD\) và tam giác vuông \(AKD\) có
+ \(AH = AK\,\left( {gt} \right)\)
+ \(AD\) chung
Suy ra \(\Delta AHD = \Delta AKD\left( {ch - cgv} \right)\) nên A đúng
Từ đó ta có \(HD = DK;\,\widehat {HAD} = \widehat {DAK}\) suy ra \(AD\) là tia phân giác góc \(HAK\) nên C đúng.
Ta có \(AH = AK\left( {gt} \right)\) và \(HA = DK\left( {cmt} \right)\) suy ra \(AD\) là đường trung trực đoạn \(HK\) nên B đúng.
Vậy cả A, B, C đều đúng.
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
-
A
\(AM \bot BC\)
-
B
\(AM\) là đường trung trực của \(BC\)
-
C
\(AM\) là đường phân giác của góc \(BAC.\)
-
D
Cả A, B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
Sử dụng định lý: Trong một tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường trung trực của tam giác đó.
Vì tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến nên \(AM\) cũng là đường cao, đường trung trực và đường phân giác của tam giác \(ABC.\)
Cho \(\Delta ABC\) nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho \(BI = AC\). Trên tia đối của tia CE lấy điểm K sao cho\(CK = AB.\)
Chọn câu đúng.
-
A
\(AI > AK\)
-
B
\(AI < AK\)
-
C
\(AI = 2AK\)
-
D
\(AI = AK\)
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất trong tam giác vuông 2 góc nhọn phụ nhau, tính chất 2 góc kề bù, dấu hiệu nhận biết tam giác vuông cân.
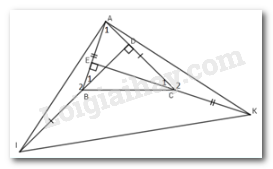
Xét \({\Delta}ABD\) có: \(\widehat {{A_1}} + \widehat {{B_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
Xét \({\Delta}AEC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)\).
Lại có: $\left\{ \begin{array}{l}\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\\\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\end{array} \right.\left( 2 \right)$ (hai góc kề bù)
Từ \(\left( 1 \right);\;\left( 2 \right) \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\) .
Xét \(\Delta ABI\) và \(\Delta KCA\) có:
\(AB = CK\left( {gt} \right)\\\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\\BI = AC\left( {gt} \right)\)
\(\Rightarrow \Delta ABI = \Delta KCA ({c - g - c})\)\( \Rightarrow AI = AK\) (2 cạnh tương ứng)
\(\Delta AIK\) là tam giác gì?
-
A
\(\Delta AIK\)là tam giác cân tại B.
-
B
\(\Delta AIK\)là tam giác vuông cân tại A.
-
C
\(\Delta AIK\)là tam giác vuông
-
D
\(\Delta AIK\)là tam giác đều
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất trong tam giác vuông 2 góc nhọn phụ nhau, tính chất 2 góc kề bù, dấu hiệu nhận biết tam giác vuông cân.
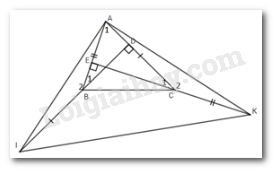
Ta có \(AI = AK\left( {cmt} \right) \Rightarrow \Delta AIK\) cân tại A (*).
\(\Delta ABI = \Delta KCA\left( {cmt} \right) \Rightarrow \widehat {AIB} = \widehat {CAK}(3)\)(2 góc tương ứng)
Xét \({\Delta}AID\) có: \(\widehat {AID} + \widehat {IAD} = {90^0}\left( 4 \right)\)(trong tam giác vuông 2 góc nhọn phụ nhau)
Từ (3) và (4)\(\Rightarrow \widehat {IAD} + \widehat {CAK} = {90^0} \Rightarrow \Delta AIK\) vuông tại A (**)
Từ (*) và (**) \(\Rightarrow \Delta AIK\)vuông cân tại $A.$
Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\) là tam giác gì?
-
A
Tam giác cân
-
B
Tam giác vuông cân
-
C
Tam giác vuông
-
D
Tam giác đều.
Đáp án của giáo viên lời giải hay : A
+) Dựa vào tính chất của các đường cao trong tam giác.
+) Dựa vào tính chất của tam giác cân.
+) Đường trung tuyến ứng với cạnh huyền của tam giác vuông bằng nửa cạnh huyền.
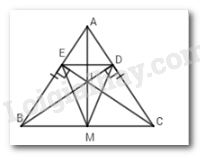
Xét \(\Delta ABC\) có $BD$ và $CE$ là hai đường cao cắt nhau tại $I$ suy ra $AI$ là đường cao của tam giác đó.
Mà $AI$ cắt $BC$ tại $M$ nên \(AM \bot BC\).
Vì \(\Delta ABC\) cân tại $A$ (gt) nên $AM$ là đường cao cũng chính là đường trung tuyến của tam giác đó. (tính chất của tam giác cân).
\( \Rightarrow BM = MC\) (tính chất đường trung tuyến)
Vì \(\left\{ \begin{array}{l}CE \bot AB\\BD \bot AC\end{array} \right. \Rightarrow \widehat {BEC} = \widehat {BDC} = {90^0}\).
Xét \({\Delta}BEC\) có $M$ là trung điểm của $BC$ nên suy ra $EM$ là trung tuyến của \({\Delta}BEC\)
\( \Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)\) (tính chất trung tuyến của tam giác vuông)
Xét \({\Delta}BDC\) có $M$ là trung điểm của $BC$ nên $DM$ là trung tuyến của \({\Delta}BDC\)
\( \Rightarrow DM = \dfrac{{BC}}{2}\left( 2 \right)\) (tính chất trung tuyến của tam giác vuông)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow EM = DM \Rightarrow \Delta EMD\) cân tại $M$ (dấu hiệu nhận biết tam giác cân).
Cho tam giác \(ABC\) nhọn có trực tâm \(H.\) Chọn câu đúng.
-
A
\(AB + AC > HA + HB + HC\)
-
B
\(AB + AC < HA + HB + HC\)
-
C
\(AB + AC = HA + HB + HC\)
-
D
\(AB + AC \le HA + HB + HC\)
Đáp án của giáo viên lời giải hay : A
- Qua \(H\) kẻ đường thẳng song song với \(AC\) cắt \(AB\) tại \(F\), kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(E\).
- Chứng minh \(\Delta AEH = \Delta HFA\,\)\( \Rightarrow EH = AF;\,AE = HF\) (hai cạnh tương ứng).
- Sử dụng quan hệ đường xiên – đường vuông góc để chứng minh \(BF > BH\),\(CE > CH\).
- Áp dụng bất đẳng thức tam giác vào \(\Delta AEH\) ta có: \(AE + EH > HA\).
Từ đó lập luận suy ra điều phải chứng minh.
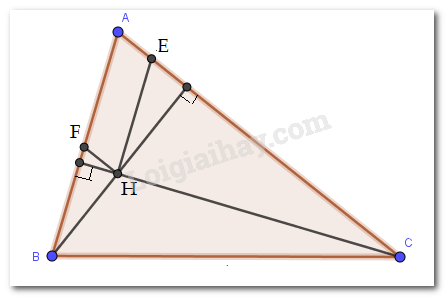
Qua \(H\) kẻ đường thẳng song song với \(AC\) cắt \(AB\) tại \(F\), kẻ đường thẳng song song với \(AB\) cắt \(AC\) tại \(E\).
Vì \(AE//HF\) (cách vẽ) nên \(\widehat {EAH} = \widehat {FHA}\) (hai góc so le trong bằng nhau)
Vì \(AF//HE\) (cách vẽ) nên \(\widehat {AHE} = \widehat {HAF}\) (hai góc so le trong bằng nhau)
Xét \(\Delta AEH\) và \(\Delta HFA\) có:
\(AH\) cạnh chung
\(\widehat {EAH} = \widehat {FHA}\,\,(cmt)\)
\(\widehat {AHE} = \widehat {HAF}\,\,(cmt)\)
\( \Rightarrow \Delta AEH = \Delta HFA\,(g.c.g)\)
\( \Rightarrow EH = AF;\,AE = HF\) (hai cạnh tương ứng).
Vì \(BH \bot AC\) và \(FH//AC\) nên \(BH \bot FH\).
Ta có: \(BF;\,BH\) lần lượt là đường xiên và đường vuông góc kẻ từ \(B\) đến \(FH\) nên \(BF > BH\) (quan hệ đường xiên – đường vuông góc).
Vì \(CH \bot AB\) và \(EH//AB\) nên \(CH \bot EH\).
Ta có: \(CE;\,CH\) lần lượt là đường xiên và đường vuông góc kẻ từ \(C\) đến \(EH\) nên \(CE > CH\) (quan hệ đường xiên – đường vuông góc).
Xét \(\Delta AEH\) có: \(AE + EH > HA\) (bất đẳng thức tam giác)
Ta có: \(AB + AC = AF + FB + AE + EC\)
\( \Rightarrow AB + AC = EH + FB + AE + EC\) (vì \(AF = EH\,(cmt)\))
\( \Rightarrow AB + AC = \left( {AE + EH} \right) + FB + EC > HA + HB + HC\).
Vậy \(AB + AC > HA + HB + HC\).
Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$\;\left( {MA < MB} \right).$ Vẽ tia $Mx$ vuông góc với $AB,$ trên đó lấy hai điểm $C$ và $D$ sao cho $MA = MC,MD = MB.$ Tia $AC$ cắt $BD$ ở $E.$ Tính số đo \(\widehat {AEB}\)
-
A
\({30^0}\)
-
B
\({45^0}\)
-
C
\({60^0}\)
-
D
\({90^0}\).
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất tam giác vuông cân, tính chất đường cao của tam giác.
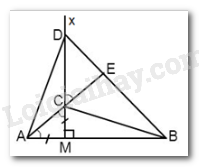
Vì $Mx \bot AB \Rightarrow \widehat {AMx} = {90^0}$
Xét $\Delta AMC$ có $\left\{ \begin{array}{l}\widehat {AMC} = {90^0}\left( {cmt} \right)\\MA = MC\left( {gt} \right)\end{array} \right. $ $\Rightarrow \widehat {MAC} = \widehat {MCA} = {45^0}$ (tính chất tam giác vuông cân)
Do đó \(\widehat {DCE} = \widehat {MCA} = {45^0}\) (đối đỉnh)
Xét $\Delta BMD$ có: $\left\{ \begin{array}{l}\widehat {BMD} = {90^0}\left( {cmt} \right)\\MB = MD\left( {gt} \right)\end{array} \right. $ $\Rightarrow \widehat {MBD} = \widehat {MDB} = {45^0}$(tính chất tam giác vuông cân)
Xét $\Delta CDE$ có: \(\widehat {CDE} = \widehat {DCE} = {45^0} \) \(\Rightarrow \widehat {CDE} + \widehat {DCE} = {90^0} \Rightarrow \widehat {DEC} = {90^0}.\)
Lại có: \(\widehat {DEC} + \widehat {AEB} = {180^0}\) (kề bù) \( \Rightarrow \widehat {AEB} = {180^0} - \widehat {DEC} = {180^0} - {90^0} = {90^0}\) .
