Bản chất lực tương tác giữa các nuclon trong hạt nhân là:
-
A
Lực tĩnh điện
-
B
Lực hấp dẫn
-
C
Lực điện từ
-
D
Lực tương tác mạnh
Đáp án của giáo viên lời giải hay : D
Lực tương tác giữa các nuclon gọi là lực hạt nhân (tương tác hạt nhân hay tương tác mạnh)
Phạm vi của lực tương tác mạnh trong hạt nhân là bao nhiêu?
-
A
10-13cm
-
B
10-8 cm
-
C
10-10 cm
-
D
Vô hạn
Đáp án của giáo viên lời giải hay : A
Lực hạt nhân chỉ phát huy tác dụng trong phạm vi kích thước hạt nhân (khoảng 10-15 m)
Độ hụt khối của hạt nhân được xác định bằng biểu thức
-
A
\(\Delta m = Z{m_n} + \left( {A - Z} \right){m_p} - {m_X}\)
-
B
\(\Delta m = {m_X} - Z{m_p} + \left( {A - Z} \right){m_n}\)
-
C
\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} + {m_X}\)
-
D
\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
Đáp án của giáo viên lời giải hay : D
Độ hụt khối của hạt nhân được xác định bằng biểu thức: \(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
Xét đồng vị Côban \(_{27}^{60}Co\) hạt nhân có khối lượng mCo = 59,934u. Biết khối lượng của các hạt: mp = 1,007276u, mn = 1,008665u. Độ hụt khối của hạt nhân đó
-
A
0,401u
-
B
0,302u
-
C
0,548u
-
D
0,544u
Đáp án của giáo viên lời giải hay : C
Vận dụng biểu thức xác định độ hụt khối của hạt nhân X: \(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
Hạt nhân \(_{27}^{60}Co\) có: \(\left\{ \begin{array}{l}Z = 27\\N = A - Z = 60 - 27 = 33\end{array} \right.\)
Độ hụt khối của hạt nhân: \(_{27}^{60}Co\) là:
\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_{Co}} = 27.1,007276 + 33.1,008665 - 59,934 = 0,548u\)
Năng lượng liên kết là
-
A
Toàn bộ năng lượng của nguyên tử gồm động năng và năng lượng nghỉ
-
B
Năng lượng tỏa ra khi các nuclon liên kết với nhau tạo thành hạt nhân
-
C
Năng lượng toàn phần của nguyên tử tính trung bình trên số nuclon
-
D
Năng lượng liên kết các eclectron và hạt nhân nguyên tử
Đáp án của giáo viên lời giải hay : B
Năng lượng liên kết của một hạt nhân là năng lượng tối thiểu cần thiết phải cung cấp để tách các nuclon hay nói cách khác là năng lượng tỏa ra khi tạo thành một hạt nhân (hay năng lượng thu vào để phá vỡ một hạt nhân thành các nuclôn riêng biệt).
Khi nói về lực hạt nhân, câu nào sau đây là không đúng?
-
A
Lực hạt nhân là lực tương tác giữa các proton với proton trong hạt nhân
-
B
Lực hạt nhân là lực tương tác giữa các proton với nơtron trong hạt nhân
-
C
Lực hạt nhân là lực tương tác giữa các nơtron với nơtron trong hạt nhân.
-
D
Lực hạt nhân chính là lực điện, tuân theo định luật Culông
Đáp án của giáo viên lời giải hay : D
D- sai vì lực hạt nhân khác bản chất với lực điện
Cho \(m_C= 12,00000u\); \(m_p= 1,00728u\); \(m_n = 1,00867u\), \(1u = 1,66058.10^{-27}kg\); \(1eV = 1,6.10^{-19}J\); \(c = 3.10^8m/s\). Năng lượng tối thiểu để tách hạt nhân \(_6^{12}C\) thành các nuclon riêng biệt bằng
-
A
72,7 MeV
-
B
89,4 MeV
-
C
44,7 MeV
-
D
8,94 MeV
Đáp án của giáo viên lời giải hay : B
+ Cácbon có Z = 6, N = 6
+ Vận dụng biểu thức tính năng lượng liên kết \({{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2}\)
+ Cácbon có số proton (Z) = số nơtron (N) = 6
Ta có:
\(\begin{array}{l}{{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_C}} \right]{c^2}\\ = \left[ {6.1,00728u + 6.1,00867u - 12,00000u} \right]{c^2}\\ = \left[ {6.1,00728 + 6.1,00867 - 12,00000} \right].u.{c^2}\\ =\left[ {6.1,00728 + 6.1,00867 - 12,00000} \right].1,{66058.10^{ - 27}}.{({3.10^8})^2}\\ = 1,{43.10^{ - 11}}J = 89,4MeV\end{array}\)
Năng lượng liên kết của \(_{10}^{20}Ne\) là $160,64 MeV$. Biết khối lượng của proton là $1,007825u$ và khối lượng của notron là $1,00866u$. Coi $1u = 931,5MeV/{c^2}$. Khối lượng nguyên tử ứng với hạt nhân \(_{10}^{20}Ne\) là:
-
A
19,986947u
-
B
19,992397u
-
C
19,996947u
-
D
19,983997u
Đáp án của giáo viên lời giải hay : B
Vận dụng biểu thức tính năng lượng liên kết \({{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2}\)
Ta có:
\(\begin{array}{l}{{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_{Ne}}} \right]{c^2} = 160,64MeV\\ = \left[ {10.1,007825u + (20 - 10).1,00866u - {m_{Ne}}} \right].{c^2}\\ \leftrightarrow (20,16485u - {m_{Ne}}){c^2} = \frac{{160,64}}{{931,5}}u{c^2}\\ \to {m_{Ne}} = 19,99239697u\end{array}\)
Tính năng lượng tỏa ra khi tạo thành \(1g\) \(_2^4He\) từ các proton và notron. Cho biết độ hụt khối của hạt nhân \(He\) là \(∆m = 0,0304u\), \(1u = 931 (MeV/c^2)\); \(1MeV = 1,6.10^{-13}(J)\). Biết số Avôgađrô \(N_A = 6,02.10^{23} mol^{-1}\), khối lượng mol của \(_2^4He\) là \(4g/mol\)
-
A
\(66.10^{10}J\)
-
B
\(66.10^{11}J\)
-
C
\(68.10^{10}J\)
-
D
\(68.10^{11}J\)
Đáp án của giáo viên lời giải hay : C
Năng lượng tỏa ra khi tạo thành 1 hạt nhân: \(\Delta m{c^2}\)
Ta có:
+ Năng lượng tỏa ra khi tạo thành 1 nguyên tử \(_2^4He\) từ các proton và nơtron: \(\Delta m{c^2}\)
+ \(1g\) \(_2^4He\) có số nguyên tử là: \(N = n.{N_A} = \dfrac{m}{M}{N_A} = \dfrac{1}{4}.6,{02.10^{23}} = 1,{505.10^{23}}\)
+ Năng lượng tỏa ra khi tạo thành \(1g\) \(_2^4He\) từ các proton và nơtron là:
\(\begin{array}{l}Q = N.\Delta m{c^2} = 1,{505.10^{23}}.0,0304.931.{c^2}\\ = 4,{26.10^{24}}MeV = 4,{26.10^{24}}.1,6.10^{-13}=6,{82.10^{11}}J\end{array}\)
Mức độ bền vững của một hạt nhân tùy thuộc vào:
-
A
Năng lượng liên kết của hạt nhân
-
B
Số nuclon
-
C
Năng lượng liên kết riêng
-
D
Số khối
Đáp án của giáo viên lời giải hay : C
Mức độ bền vững của một hạt nhân tùy thuộc vào năng lượng liên kết riêng
Hạt nhân càng bền vững khi có
-
A
Số nuclon càng nhỏ
-
B
Số nuclon càng lớn
-
C
Năng lượng liên kết càng lớn
-
D
Năng lượng liên kết riêng càng lớn
Đáp án của giáo viên lời giải hay : D
Mức độ bền vững của một hạt nhân tùy thuộc vào năng lượng liên kết riêng
Hạt nhân càng bền vững khi có năng lượng liên kết riêng càng lớn
Năng lượng liên kết riêng được xác định bằng biểu thức nào dưới đây:
-
A
\(\varepsilon = {{\rm{W}}_{lk}}A\)
-
B
\(\varepsilon = \frac{A}{{{{\rm{W}}_{lk}}}}\)
-
C
\(\varepsilon = \frac{{{{\rm{W}}_{lk}}}}{A}\)
-
D
\(\varepsilon = {{\rm{W}}_{lk}}\)
Đáp án của giáo viên lời giải hay : C
Xem lí thuyết mục 2
Năng lượng liên kết riêng được xác định bằng biểu thức: \(\varepsilon = \frac{{{{\rm{W}}_{lk}}}}{A}\)
Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclon của hạt nhân X lớn hơn số nuclon của hạt nhân Y thì
-
A
Hạt nhân Y bền vững hơn hạt nhân X
-
B
Hạt nhân X bền vững hơn hạt nhân Y
-
C
Năng lượng liên kết riêng của hai hạt bằng nhau
-
D
Năng lượng liên kết của hạt nhân X lớn hơn năng lượng liên kết của hạt nhân Y
Đáp án của giáo viên lời giải hay : A
+ Vận dụng biểu thức tính năng lượng liên kết
+ Vận dụng biểu thức tính năng lượng liên kết riêng
Ta có:
+ Hai hạt nhân có độ hụt khối bằng nhau => năng lượng liên kết của 2 hạt nhân bằng nhau và bằng\(\Delta m{c^2}\)
+ Mặt khác, ta có năng lượng liên kết riêng: \(\varepsilon = \frac{{{{\rm{W}}_{lk}}}}{A}\)
Theo đầu bài, ta có số nuclon của hạt nhân X lớn hơn số nuclon của hạt nhân Y => năng lượng liên kết riêng của hạt nhân X nhỏ hơn năng lượng liên kết riêng của hạt nhân Y
=> Hạt nhân Y bền vững hơn hạt nhân X
Cho ba hạt nhân X, Y và Z có số nuclon tương ứng là \({A_X},{\rm{ }}{A_Y},{\rm{ }}{A_Z}\) với \({A_X} = {\rm{ }}2{A_Y} = {\rm{ }}0,5{A_Z}\) . Biết năng lượng liên kết của từng hạt nhân tứng ứng là \(\Delta {E_X},\Delta {E_{Y,}}\Delta {E_Z}\) với \(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y}\) . Sắp xếp các hạt nhân này theo thứ tự tính bền vững giảm dần là:
-
A
Y, X, Z
-
B
Y, Z, X
-
C
X, Y, Z
-
D
Z, X, Y
Đáp án của giáo viên lời giải hay : A
Ta có, năng lượng liên kết riêng của các hạt nhân là:
\({\varepsilon _Y} = \dfrac{{\Delta {E_Y}}}{{{A_Y}}}\)
\({\varepsilon _X} = \dfrac{{\Delta {E_X}}}{{{A_X}}} = \dfrac{{\Delta {E_X}}}{{2{A_Y}}} = \dfrac{{\Delta {E_X}}}{{2\Delta {E_Y}}}{\varepsilon _Y}\)
\({\varepsilon _Z} = \dfrac{{\Delta {E_Z}}}{{{A_Z}}} = \dfrac{{\Delta {E_Z}}}{{4{A_Y}}} = \dfrac{{\Delta {E_Z}}}{{4\Delta {E_Y}}}{\varepsilon _Y}\)
Theo đề bài, ta có: \(\Delta {E_Z} < \Delta {E_X} < \Delta {E_Y} \to {\varepsilon _Y} > {\varepsilon _X} > {\varepsilon _Z}\)
=> các hạt nhân được sắp xếp theo thứ tự giảm dần tính bền vững là: \(Y, X, Z\)
Cho khối lượng của proton; nơtron; \(_{18}^{40}{\rm{Ar; }}_3^6Li\)lần lượt là 1,0073u; 1,0087u, 39,9525u, 6,0145u và 1u = 931,5MeV/c2. So với năng lượng liên kết riêng của hạt nhân \(_3^6Li\) thì năng lượng liên kết riêng của hạt nhân \(_{18}^{40}{\rm{Ar}}\)
-
A
Lớn hơn một lượng là 5,20 MeV/nuclon
-
B
Lớn hơn một lượng là 3,42 MeV/nuclon
-
C
Nhỏ hơn một lượng là 3,42 MeV/nuclon
-
D
Nhỏ hơn một lượng là 5,20 MeV/nuclon
Đáp án của giáo viên lời giải hay : B
+ Vận dụng biểu thức tính năng lượng liên kết: \({{\rm{W}}_{lk}} = \left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2}\)
+ Vận dụng biểu thức tính năng lượng liên kết riêng: \(\varepsilon = \frac{{{{\rm{W}}_{lk}}}}{A}\)
Ta có, năng lượng liên kết riêng: \(\varepsilon = \frac{{{{\rm{W}}_{lk}}}}{A} = \frac{{\left[ {Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2}}}{A}\)
=> Năng lượng liên kết riêng của Ar và Li là:
\(\begin{array}{l}{\varepsilon _{{\rm{Ar}}}} = \frac{{\left[ {18.1,0073 + \left( {40 - 18} \right)1,0087 - 39,9525} \right]{c^2}}}{{40}}\\ = 9,{2575.10^{ - 3}}u{c^2}/nuclon = 8,62MeV/nuclon\end{array}\)
\(\begin{array}{l}{\varepsilon _{Li}} = \frac{{\left[ {3.1,0073 + \left( {6 - 3} \right)1,0087 - 6,0145} \right]{c^2}}}{6}\\ = 5,{583.10^{ - 3}}u{c^2}/nuclon = 5,2MeV/nuclon\end{array}\)
=> So với năng lượng liên kết riêng của hạt nhân \(_3^6Li\) thì năng lượng liên kết riêng của hạt nhân \(_{18}^{40}{\rm{Ar}}\)lớn hơn một lượng là:\(8,62 - 5,2 = 3,42MeV/nuclon\)
Các hạt nhân Đơteri \(_1^2H\), Triti \(_1^3H\), Heli \(_2^4He\) có năng lượng liên kết lần lượt là 2,22 MeV, 8,49 MeV và 28,16 MeV. Các hạt nhân trên được sắp xếp theo thứ tự giảm dần về độ bền vững của hạt nhân 1à:
-
A
\(_1^2H\);\(_2^4He\); \(_1^3H\)
-
B
\(_1^2H\); \(_1^3H\);\(_2^4He\)
-
C
\(_2^4He\); \(_1^3H\);\(_1^2H\)
-
D
\(_1^3H\);\(_2^4He\); \(_1^2H\)
Đáp án của giáo viên lời giải hay : C
Ta có năng lượng liên kết riêng ứng với các hạt nhân là:
+ \({\varepsilon _D} = \frac{{2,22}}{2} = 1,11MeV/nuclon\)
+ \({\varepsilon _T} = \frac{{8,49}}{3} = 2,83MeV/nuclon\)
+ \({\varepsilon _{He}} = \frac{{28,16}}{4} = 7,04MeV/nuclon\)
Ta thấy: \({\varepsilon _{He}} > {\varepsilon _T} > {\varepsilon _D}\)=> các hạt nhân trên được sắp xếp theo thứ tự giảm dần về độ bền vững của hạt nhân 1à: \(_2^4He\); \(_1^3H\);\(_1^2H\)
Trong các hạt nhân: \(_2^4He;{\rm{ }}_3^7Li;{\rm{ }}_{26}^{56}F{\rm{e}};{\rm{ }}_{92}^{235}U\). Hạt nhân bền vững nhất là:
-
A
\(_{92}^{235}U\)
-
B
\({\rm{ }}_{26}^{56}F{\rm{e}}\)
-
C
\(_3^7Li\)
-
D
\(_2^4He\)
Đáp án của giáo viên lời giải hay : B
Ta có: Các hạt nhân bền vững có \(\dfrac{{{{\rm{W}}_{lk}}}}{A}\) lớn nhất vào cỡ 8,8 MeV/nuclon; đó là những hạt nhân nằm khoảng giữa của bảng tuần hoàn ứng với \(50 < A < 80\)
=> hạt nhân bền vững nhất trong các hạt nhân trên là \({\rm{ }}_{26}^{56}F{\rm{e}}\)
Hạt nhân đơteri \({}_1^2D\)có năng lượng liên kết là \(2,2356 MeV\). Năng lượng liên kết riêng của hạt nhân này bằng
-
A
\(1,1178 MeV/nuclon\).
-
B
\(4,4712 MeV/nuclon\).
-
C
\(2,2356 MeV/nuclon\).
-
D
\(0,7452 MeV/nuclon\).
Đáp án của giáo viên lời giải hay : A
Năng lượng liên kết riêng của hạt nhân: \({{\rm{W}}_{LKR}} = \dfrac{{{{\rm{W}}_{LK}}}}{A}\)
\({{\rm{W}}_{LKR}} = \dfrac{{{{\rm{W}}_{LK}}}}{A} = \dfrac{{2,2356}}{2} = \)\(1,1178(MeV)\)
Nguyên tử sắt \({}_{26}^{56}Fe\) có khối lượng là 55,934939u. Biết:
\(\begin{array}{l}
{m_n} = 1,00866u;{m_p} = 1,00728u;\\
{m_e} = 5,{486.10^{ - 4}}u;1u = 931,5MeV/{c^2}
\end{array}\)
Tính năng lượng liên kết riêng của hạt nhân sắt?
-
A
7,878MeV/nucℓon
-
B
7,878eV/nucℓon
-
C
8,789MeV/nucℓon
-
D
8,789eV/nucℓon
Đáp án của giáo viên lời giải hay : C
Năng lượng liên kết: \({W_{lk}} = \Delta m.{c^2} = \left[ {Z.{m_p} + \left( {A - Z} \right){m_n} - {m_{hn}}} \right]{c^2}\)
Năng lượng liên kết riêng: \(\varepsilon = \dfrac{{{W_{lk}}}}{A}\)
Khối lượng hạt nhân: \({m_{hn}} = {m_{nguyen\,tu}} - Z.{m_e}\)
Khối lượng của hạt nhân \({}_{26}^{56}Fe\) là:
\(\begin{array}{l}{m_{hn}} = {m_{nguyen\,tu}} - Z.{m_e}\\\,\,\,\,\,\,\,\,\, = 55,934939 - 26.5,{486.10^{ - 4}} = 55,9206754u\end{array}\)
Năng lượng liên kết của hạt nhân \({}_{26}^{56}Fe\) là:
\(\begin{array}{l}{W_{lk}} = \Delta m.{c^2} = \left[ {Z.{m_p} + \left( {A - Z} \right){m_n} - {m_{hn}}} \right]{c^2}\\\,\,\,\,\,\,\,\, = \left[ {26.1,00728 + \left( {56 - 26} \right).1,00866 - 55,9206754} \right]u{c^2}\\\,\,\,\,\,\,\,\, = 0,5284046.931,5\,\,MeV = 492,209MeV\end{array}\)
Năng lượng liên kết riêng của hạt nhân sắt:
\(\varepsilon = \dfrac{{{W_{lk}}}}{A} = \dfrac{{492,209\,}}{{56}} = 8,789\dfrac{{MeV}}{{nuclon}}\)
Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclon của hạt nhân X lớn hơn số nuclôn của hạt nhân Y thì:
-
A
năng lượng liên kết của hạt nhân X lớn hơn năng lượng liên kết của hạt nhân Y.
-
B
năng lượng liên kết riêng của hai nhạt nhân bằng nhau.
-
C
hạt nhân Y bền vững hơn hạt nhân X.
-
D
hạt nhân X bền vững hơn hạt nhân Y.
Đáp án của giáo viên lời giải hay : C
+ Năng lượng liên kết: \({W_{lk}} = \Delta m.{c^2}\)
+ Năng lượng liên kết riêng: \(\varepsilon = \dfrac{{{W_{lk}}}}{A} = \dfrac{{\Delta m.{c^2}}}{A}\)
+ Hạt nhân có năng lượng liên kết riêng càng lớn thì hạt nhân càng bền vững.
+ Năng lượng liên kết: \(\left\{ \begin{array}{l}{W_{lkX}} = \Delta {m_X}.{c^2}\\{W_{lkY}} = \Delta {m_Y}.{c^2}\\\Delta {m_X} = \Delta {m_Y}\end{array} \right. \Rightarrow {W_{lkX}} = {W_{lkY}} = {W_{lk}}\)
+ Năng lượng liên kết riêng: \(\left\{ \begin{array}{l}{\varepsilon _X} = \dfrac{{{W_{lk}}}}{{{A_X}}}\\{\varepsilon _Y} = \dfrac{{{W_{lk}}}}{{{A_Y}}}\\{A_X} > {A_Y}\end{array} \right. \Rightarrow {\varepsilon _X} < {\varepsilon _Y}\)
Vậy hạt nhân Y bền vững hơn hạt nhân X.
Phản ứng nhiệt hạch D + D → X + n + 3,25MeV. Biết độ hụt khối của D là DmD = 0,0024u và 1uc2 = 931MeV. Năng lượng liên kết của hạt nhân X là
-
A
9,24 MeV
-
B
5,22 MeV
-
C
7,72 MeV
-
D
8,52 MeV
Đáp án của giáo viên lời giải hay : C
Nhiệt lượng tỏa ra của phản ứng: \({Q_{toa}} = \left( {\Delta {m_{sau}} - \Delta {m_{trc}}} \right){c^2}\)
Năng lượng liên kết của hạt nhân X: \({W_{lkX}} = \Delta {m_X}.{c^2}\)
Năng lượng tỏa ra của phản ứng:
\(\begin{array}{l}{Q_{toa}} = \left( {\Delta {m_{sau}} - \Delta {m_{trc}}} \right){c^2} \Leftrightarrow \left( {\Delta {m_X} - 2.\Delta {m_D}} \right)c = 3,25MeV\\ \Rightarrow {W_{lkX}} = \Delta {m_X}.{c^2} = 3,25 + 2.\Delta {m_D}.{c^2} = 3,25 + 2.0,0024.931 = 7,72MeV\end{array}\)
Hạt nhân Đơteri \({}_1^2D\) có khối lượng 2,0136u. Năng lượng liên kết của hạt nhân Đơteri \({}_1^2D\) bằng
-
A
1,86MeV
-
B
2,18MeV
-
C
0,67MeV
-
D
2,81MeV
Đáp án của giáo viên lời giải hay : B
Công thức tính năng lượng liên kết:
\({{\rm{W}}_{lk}} = \left[ {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right].{c^2} = \left[ {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right].{c^2}.931\left( {MeV} \right)\)
Năng lượng liên kết của hạt nhân Doteri bằng:
\(\begin{array}{l}
{{\rm{W}}_{lk}} = \left[ {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right].{c^2}\\
\,\,\,\,\,\,\,\,\, = \left[ {Z.{m_p} + (A - Z).{m_n} - {m_X}} \right].{c^2}.931\left( {MeV} \right)\\
\,\,\,\,\,\,\,\,\, = \left[ {1.1,0073 + (2 - 1).1,0086 - 2,0136} \right].931,5 = 2,18meV
\end{array}\)
Cho khối lượng của prôtôn; nơtron;\({}_{18}^{40}\text{Ar};{}_{3}^{6}Li\) lần lượt là 1,0073u; 1,0087u; 39,9525u; 6,0145u và 1u = 931,5 MeV/c2. So với năng lượng liên kết riêng của hạt nhân \({}_{3}^{6}Li\) thì năng lượng liên kết riêng của hạt nhân \({}_{18}^{40}\text{Ar}\)
-
A
lớn hơn một lượng là 5,20 MeV.
-
B
lớn hơn một lượng là 3,42 MeV.
-
C
nhỏ hơn một lượng là 5,20 MeV.
-
D
nhỏ hơn một lượng là 3,42 MeV.
Đáp án của giáo viên lời giải hay : B
Năng lượng liên kết riêng của hạt nhân : \({{\text{W}}_{lkr}}=\frac{{{\text{W}}_{lk}}}{A}=\frac{\left[ Z.{{m}_{p}}+\left( A-Z \right).{{m}_{n}}-m \right]{{c}^{2}}}{A}\)
Năng lượng liên kết riêng của hạt nhân \({}_{18}^{40}\text{Ar}\)\({{\text{W}}_{LK(\text{Ar})}}=\left[ \left( 18{{m}_{p}}+22{{m}_{n}} \right)-{{m}_{Ar}} \right]{{c}^{2}}=344,93445(MeV)\to {{\text{W}}_{LKR(\text{Ar})}}=\frac{{{\text{W}}_{LK(\text{Ar})}}}{{{A}_{\text{Ar}}}}\approx 8,62336(MeV/nuclon)\)
Năng lượng liên kết riêng của hạt nhân \({}_{3}^{6}Li\):
\({{\rm{W}}_{LK(Li)}} = \left[ {\left( {3{m_p} + 3{m_n}} \right) - {m_{Li}}} \right]{c^2} = 31,20525(MeV) \to {{\rm{W}}_{LKR(Li)}} = \frac{{{{\rm{W}}_{LK(Li)}}}}{{{A_{Li}}}} \approx 5,200875(MeV/nuclon)\)
\(\to \Delta {{\text{W}}_{LKR}}={{\text{W}}_{LKR(Ar)}}-{{\text{W}}_{LKR(Li)}}\approx 3,42248625(MeV/nuclon)\)
Hạt nhân Đơteri \({}_1^2D\) có khối lượng \(2,0136{\rm{ }}u.\) Biết khối lượng của prôtôn là \(1,0073u\) và khối lượng của nơtrôn là \(1,0087{\rm{ }}u.\) Độ hụt khối của hạt nhân \({}_1^2D\) bằng
-
A
\(0,0024u\).
-
B
\(0,0012u.\)
-
C
\(0,0032u.\)
-
D
\(0,0036u.\)
Đáp án của giáo viên lời giải hay : A
Sử dụng công thức tính độ hụt khối: \(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}.\)
Độ hụt khối của hạt nhân \({}_1^2D\) là:
\(\Delta m = Z{m_p} + \left( {A - Z} \right){m_n} - {m_X}\)
\( = 1,0073u + (2 - 1).1,0087u - 2,0136u\)
\( = 0,0024u\)
Hạt nhân \(_{92}^{235}U\) có độ hụt khối \(1,91519u\). Biết \(1u{c^2} = 931,5MeV\). Năng lượng liên kết của hạt nhân này có giá trị xấp xỉ bằng
-
A
1784 MeV.
-
B
1990MeV.
-
C
1820MeV.
-
D
1597MeV.
Đáp án của giáo viên lời giải hay : A
Công thức tính năng lượng liên kết:
\({{\rm{W}}_{lk}} = \left[ {Z.{m_p} + \left( {A - Z} \right){m_n} - {m_X}} \right]{c^2} = \Delta m{c^2}\)
Năng lượng liên kết của hạt nhân có giá trị:
\({{\rm{W}}_{lk}} = \Delta m{c^2} = 1,91519u{c^2} = 1,91519.931,5 = 1784MeV\)
Trên hình là đồ thị biểu diễn sự biến thiên của năng lượng liên kết riêng (trục tung, theo đơn vị MeV/nuclôn) theo số khối (trục hoành) của các hạt nhân nguyên tử. Phát biểu nào sau đây đúng?
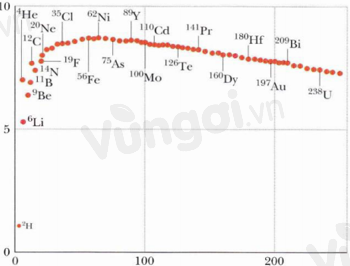
-
A
Hạt nhân \(^{238}U\) bền vững nhất.
-
B
Hạt nhân \(^{35}Cl\) bền vững hơn hạt nhân \(^{56}Fe\)
-
C
Hạt nhân \(^6Li\) bền vững nhất.
-
D
Hạt nhân \(^{62}Ni\) bền vững nhất.
Đáp án của giáo viên lời giải hay : D
+ Năng lượng liên kết tính cho một nuclon được gọi là năng lượng liên kết riêng, đặc trưng cho độ bền vững của hạt nhân.
+ Hạt nhân có năng lượng liên kết riêng càng lớn thì càng bền vững.
Từ đồ thị ta thấy hạt nhân \(^{62}Ni\) có năng lượng liên kết riêng lớn nhất
\( \Rightarrow \) Hạt nhân \(^{62}Ni\) bền vững nhất.
