Hình lăng trụ đứng tam giác có tất cả bao nhiêu cạnh?
-
A
9
-
B
6
-
C
12
-
D
8
Đáp án của giáo viên lời giải hay : A
Đặc điểm hình lăng trụ đứng tam giác

Các cạnh của hình lăng trụ đứng tam giác là: \(AB,\,\,AC,\,\,BC,\,\,{A_1}{B_1},\)\({A_1}{C_1},\,\,{B_1}{C_1},\,\,A{A_1},\,\,\,B{B_1},\,C{C_1}\)
Vậy hình lăng trụ đứng tam giác có tất cả \(9\) cạnh.
Phát biểu nào sau đây là đúng?
-
A
Các mặt bên của hình lăng trụ đứng là các hình chữ nhật.
-
B
Các mặt bên của hình lăng trụ đứng là các hình thang cân.
-
C
Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật.
-
D
Các mặt đáy của hình lăng trụ đứng là các hình tam giác.
Đáp án của giáo viên lời giải hay : C
Đặc điểm hình lăng trụ đứng tam giác
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Tính thể tích của hình lăng trụ đứng có chiều cao \(20cm\), đáy là một tam giác vuông có các cạnh góc vuông lần lượt là \(8cm\) và \(10cm\).
-
A
\(800c{m^3}\)
-
B
\(400c{m^3}\)
-
C
\(600c{m^3}\)
-
D
\(500c{m^3}\)
Đáp án của giáo viên lời giải hay : A
+ Tính diện tích đáy là tam giác vuông: Sđáy = \(\frac{1}{2}\). Cạnh góc vuông . cạnh góc vuông
+ Tính thể tích: V = Sđáy . h
Diện tích đáy của hình lăng trụ đứng là:\(\dfrac{1}{2}.8.10=40 cm^3\)
Thể tích của hình lăng trụ đứng là: \( 40.20= 800\,\,\left( {c{m^3}} \right)\)
Vậy thể tích của hình lăng trụ đứng là \(800\,\,\left( {c{m^3}} \right)\).
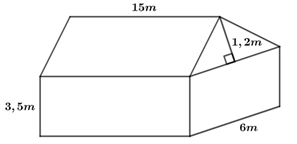
Tính thể tích phần không gian của một ngôi nhà dạng một lăng trụ đứng theo các kích thước đã cho trong hình.
-
A
369 m3
-
B
315 m3
-
C
327 m3
-
D
423 m3
Đáp án của giáo viên lời giải hay : A
Tính tổng của thể tích hình lăng trụ và thể tích hình hộp chữ nhật.
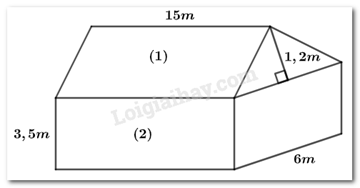
Theọ hình vẽ, ngôi nhà gồm hai phần: một phần là lăng trụ đứng có đáy là tam giác cân cạnh đáy bằng \(6m\), chiều cao đáy \(1,2m\), chiều cao lăng trụ bằng \(15m\); phần còn lại là hình hộp chữ nhật có kích thước đáy là \(6m\) và \(15m\), chiều cao \(3,5m\).
Thể tích hình lăng trụ tam giác là:
\({V_1} = \frac{1}{2}.6.1,2.15 = 54{\rm{ }}\left( {{m^3}} \right)\)
Thể tích hình hộp chữ nhật là:
\({V_2} = 6.15.3,5 = 315{\rm{ }}\left( {{m^3}} \right)\)
Thể tích phần không gian bên trong của cả ngôi nhà là:
\(V = {V_1} + {V_2} = 54 + 315 = 369{\rm{ }}\left( {{m^3}} \right)\)
Thể tích phần không gian của ngôi nhà là \(369{\rm{ }}\left( {{m^3}} \right)\)
Một chiếc đèn lồng có dạng hình lăng trụ đứng, chiều cao \(40cm\) và đáy là lục giác đều cạnh \(18cm\). Nếu giữ nguyên chiều cao của đèn thì phải giảm độ dài cạnh đáy bao nhiêu lần để thể tích của đèn giảm đi hai lần.
-
A
\(\sqrt 2 \)lần
-
B
2 lần
-
C
4 lần
-
D
8 lần
Đáp án của giáo viên lời giải hay : A
Lập tỉ số thể tích trước và sau khi giảm độ dài cạnh đáy.
Diện tích đáy đèn là: \(S = \frac{{{a^2}\sqrt 3 }}{4}.6\)\( = \frac{{{{18}^2}\sqrt 3 }}{4}.6 = 486\sqrt 3 \,\,\left( {c{m^2}} \right)\)
Gọi \(a\) và \(b\) lần lượt là độ dài cạnh đáy đèn lồng trước và sau khi giảm thể tích.
Gọi \({S_1}\) và \({S_2}\) là các diện tích đáy tương ứng. Khi đó: \({V_1} = {S_1}.h;\,\,{V_2} = {S_2}.h\)
Ta có: \(\frac{{{V_1}}}{{{V_2}}} = 2 \Leftrightarrow \frac{{{S_1}.h}}{{{S_2}.h}} = 2\)\( \Leftrightarrow \frac{{{S_1}}}{{{S_2}}} = 2\)
\( \Leftrightarrow \frac{{{a^2}\sqrt 3 .6}}{4}:\frac{{{b^2}\sqrt 3 .6}}{4} = 2\)\( \Leftrightarrow {a^2}:{b^2} = 2\)\( \Leftrightarrow a:b = \sqrt 2 \)
Vậy độ dài cạnh đáy phải giảm đi \(\sqrt 2 \) lần.
Hình lăng trụ đứng tứ giác có đáy là hình thang cân có bao nhiêu mặt bên?
-
A
\(3\)
-
B
\(4\)
-
C
\(5\)
-
D
\(6\)
Đáp án của giáo viên lời giải hay : B
Đặc điểm lăng trụ đứng tứ giác
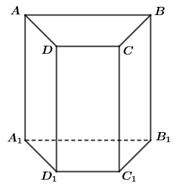
Hình lăng trụ đứng \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có đáy \({A_1}{B_1}{C_1}{D_1}\) là hình thang cân, có các mặt bên là: \(AD{D_1}{A_1};\,\,AB{B_1}{A_1};\,\,DC{C_1}{D_1};\,\,BC{C_1}{B_1}\)
Vậy hình lăng trụ đứng tứ giác đáy là hình thang cân có 4 mặt bên.
Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước \(3cm,\,\,8cm\). Chiều cao của hình lăng trụ đứng là \(2cm\). Diện tích xung quanh của hình lăng trụ đứng là
-
A
\(44c{m^2}\)
-
B
\(24c{m^2}\)
-
C
\(48c{m^2}\)
-
D
\(22c{m^2}\)
Đáp án của giáo viên lời giải hay : A
+ Tính chu vi đáy là hình chữ nhật
+ Tính Sxq = chu vi đáy . chiều cao
Chu vi đáy của hình lăng trụ đứng là: \(\left( {8 + 3} \right).2 = 22\left( {cm} \right)\)
Diện tích xung quanh của hình lăng trụ đứng là: \({S_{xq}} = C.h = 22.2 = 44\,\,\left( {c{m^2}} \right)\)
Vậy diện tích xung quanh của hình lăng trụ đứng là \(44\,\,\left( {c{m^2}} \right)\)
Cho hình lăng trụ đứng có diện tích xung quanh bằng 336 cm2, chiều cao 14 cm. Khi đó, chu vi đáy của hình lăng trụ đứng là:
-
A
\(12cm\)
-
B
\(24cm\)
-
C
\(36cm\)
-
D
\(48cm\)
Đáp án của giáo viên lời giải hay : B
Từ công thức Sxq = Chu vi đáy . chiều cao suy ra chu vi đáy
Chu vi đáy của hình lăng trụ đứng đó là:
C = Sxq : h = 336 : 14 = 24 (cm)
Một hình lăng trụ đều (tức là lăng trụ có đáy là đa giác đều) có tất cả \(18\) cạnh, mỗi cạnh dài \(6\sqrt 3 \) cm. Tính thể tích của hình lăng trụ đó.
-
A
864 cm3
-
B
1944 cm3
-
C
2916 cm3
-
D
1122 cm3
Đáp án của giáo viên lời giải hay : C
Để tìm được thể tích lăng trụ đứng khi đã biết chiều cao, ta cần tính diện tích đáy.
Thể tích = diện tích đáy . chiều cao
Gọi số cạnh của một đáy là \(n\). Khi đó số cạnh bên là \(n\).
Suy ra, tổng số cạnh của hình lăng trụ đứng là \(n + n + n = 3n\).
Theo đề bài, hình lăng trụ đều có tất cả 18 cạnh, ta có: \(3n = 18 \Rightarrow n = 6.\)
Vậy hình lăng trụ đứng đã cho là hình lăng trụ lục giác đều.
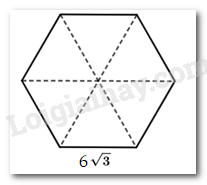
Có thể coi diện tích đáy là tổng diện tích của 6 tam giác đều, mỗi cạnh bằng \(6\sqrt 3 \) cm.
Do đó diện tích đáy là: \(S = \frac{{{{\left( {6\sqrt 3 } \right)}^2}.\sqrt 3 }}{4}.6 = 162\sqrt 3 \) ( cm2)
Thể tích hình lăng trụ là: \(V = S.h = 162\sqrt 3 .6\sqrt 3 \)= 2916 ( cm3)
Thể tích hình lăng trụ là 2916 ( cm3).
Một hình lăng trụ đứng có đáy là hình chữ nhật có diện tích xung quanh bằng tổng diện tích hai đáy, chiều cao bằng \(6cm\). Một kích thước của đáy bằng \(10cm\), tính kích thước còn lại.
-
A
\(15cm\)
-
B
\(20cm\)
-
C
\(25cm\)
-
D
\(10cm\)
Đáp án của giáo viên lời giải hay : A
Sử dụng công thức diện tích xung quanh của hình lăng trụ đứng:
\({S_{xq}} = 2p.h\)
Trong đó, \(p\) là nửa chu vi đáy ; \(h\) là chiều cao
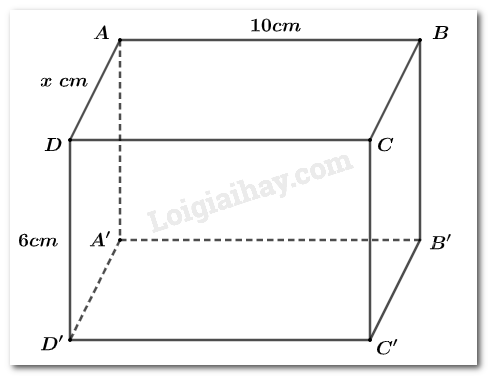
Đặt \(AD = x\left( {cm} \right)\).
Diện tích xung quanh của hình lăng trụ là: \({S_{xq}} = 2p.h\)\( = 2.\left( {10 + {\rm{ }}x} \right).6\)\( = 12.\left( {10 + {\rm{ }}x} \right)\,\,\left( {c{m^2}} \right)\)
Tổng diện tích hai đáy của hình lăng trụ là: \(2.10x = 20x\,\,(c{m^2})\)
Theo đề bài, ta có diện tích xung quanh bằng tổng diện tích hai đáy
\(\begin{array}{l} \Rightarrow 12.\left( {10 + x} \right) = 20x\\ \Leftrightarrow 120 + 12x = 20x\\ \Leftrightarrow x = 15\,\left( {cm} \right)\end{array}\)
\( \Rightarrow AD = 15\left( {cm} \right)\)
Vậy kích thước còn lại của đáy bằng 15 cm.
