Số vô tỉ là số:
-
A
Số thập phân vô hạn tuần hoàn
-
B
Số thập phân hữu hạn
-
C
Số thập phân vô hạn không tuần hoàn
-
D
Số hữu tỉ
Đáp án của giáo viên lời giải hay : C
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Số nào sau đây là 1 số vô tỉ?
-
A
0
-
B
Căn bậc hai số học của 15
-
C
Căn bậc hai số học của 16
-
D
Căn bậc hai số học của 0,25
Đáp án của giáo viên lời giải hay : B
Tìm căn bậc hai số học của các số.
Số 0 không là số vô tỉ
Ta có: 16 = 42 nên 4 là căn bậc hai số học của 16.
0,25 = (0,5)2 nên 0,5 là căn bậc hai số học của 0,25.
Căn bậc hai số học của 15 là \(\sqrt {15} \) là 1 số thập phân vô hạn không tuần hoàn nên là số vô tỉ.
Tính độ dài cạnh của hình vuông có diện tích là 0,49 ha.
-
A
49 m
-
B
0,7 km
-
C
70 m
-
D
24,01 m
Đáp án của giáo viên lời giải hay : C
Tìm căn bậc hai số học của một số.
Chú ý đơn vị.
Đổi 0,49 ha = 4900 m2
Độ dài các cạnh của hình vuông là: \(\sqrt {4900} = 70(m)\)
Số a có căn bậc hai số học là \(\dfrac{4}{9}\)
Tìm số a.
-
A
\(\dfrac{{16}}{{81}}\)
-
B
\(\dfrac{2}{3}\)
-
C
\(\dfrac{9}{4}\)
-
D
\(\dfrac{{ - 2}}{3}\)
Đáp án của giáo viên lời giải hay : A
Số x là căn bậc hai số học của số a khi a > 0 và a = x2
\(a = {\left( {\dfrac{4}{9}} \right)^2} = \dfrac{{16}}{{81}}\)
Bác Long cần lát nền 1 căn phòng có diện tích là 64 m2. Mỗi viên gạch bác định dùng để lát phòng có dạng hình vuông cạnh 40 cm. Biết mỗi viên gạch có giá 13 000 đồng. Tính số tiền bác cần dùng để mua gạch lát phòng?
-
A
5,2 triệu đồng
-
B
52 triệu đồng
-
C
1,3312 triệu đồng
-
D
3,328 triệu đồng
Đáp án của giáo viên lời giải hay : A
Tính diện tích 1 viên gạch
Tính số viên gạch cần dùng
Tính số tiền cần dùng để mua gạch
Đổi 40 cm = 0,4 m
Diện tích 1 viên gạch là: 0,4 . 0,4 = 0,16 (m2)
Số viên gạch cần dùng là: 64 : 0,16 = 400 ( viên)
Số tiền cần dùng để mua gạch là:
400 . 13 000 = 5 200 000 ( đồng)
Tính: \(\sqrt {{{( - 3)}^2}} .\dfrac{2}{3} + \sqrt {{4^4}} .{\left( {\dfrac{3}{4}} \right)^2}\)
-
A
7
-
B
\(\dfrac{1}{4}\)
-
C
\(\dfrac{{17}}{4}\)
-
D
11
Đáp án của giáo viên lời giải hay : D
Tính \(\sqrt {{a^2}} = a(a \ge 0)\)
\(\begin{array}{l}\sqrt {{{( - 3)}^2}} .\dfrac{2}{3} + \sqrt {{4^4}} .{\left( {\dfrac{3}{4}} \right)^2}\\ = \sqrt {{3^2}} .\dfrac{2}{3} + \sqrt {{{16}^2}} .{\left( {\dfrac{3}{4}} \right)^2}\\ = 3.\dfrac{2}{3} + 16.\dfrac{9}{{16}}\\ = 2 + 9\\ = 11\end{array}\)
Người ta dự định trồng hoa xung quanh mảnh đất hình vuông có diện tích là 196 m2. Biết hai cây liên tiếp cách nhau 50 cm. Tính số cây hoa trồng được.
-
A
112 cây
-
B
108 cây
-
C
116 cây
-
D
128 cây
Đáp án của giáo viên lời giải hay : A
+ Tính cạnh hình vuông: Hình vuông có diện tích a thì có cạnh là \(\sqrt a \)
+ Tính số cây trồng được trên 1 cạnh hình vuông = cạnh hình vuông : khoảng cách giữa 2 cây + 1
+ Tính số cây trồng được = 4 . số cây trồng được trên 1 cạnh - 4 cây trồng ở 4 đỉnh đã được tính 2 lần.
Cạnh mảnh đất hình vuông là:
\(\sqrt {196} = 14\) ( cm)
Đổi 50 cm = 0,5 m
Số cây hoa trồng được trên 1 cạnh là: 14 : 0,5 + 1 = 29 ( cây)
Do trồng cây trên 4 cạnh hình vuông và 4 cây trồng trên 4 đỉnh của hình vuông đã được tính 2 lần nên
Số cây hoa trồng được là:
29 . 4 – 4 = 112 ( cây)
Tính giá trị của \(\sqrt {20} - \sqrt {12} :\sqrt 3 \) rồi làm tròn kết quả đến hàng phần trăm.
-
A
2,5
-
B
2,47
-
C
0,47
-
D
0,58
Đáp án của giáo viên lời giải hay : B
Học sinh sử dụng máy tính cầm tay để tính, chú ý thứ tự thực hiện phép tính
Ta có: \(\sqrt {20} - \sqrt {12} :\sqrt 3 \) = 2,472…\( \approx \)2,47
So sánh: \(\sqrt {14} + \sqrt 8 \) với \(\sqrt {50} \)
-
A
\(\sqrt {14} + \sqrt 8 \) > \(\sqrt {50} \)
-
B
\(\sqrt {14} + \sqrt 8 \) < \(\sqrt {50} \)
-
C
\(\sqrt {14} + \sqrt 8 \) = \(\sqrt {50} \)
-
D
\(\sqrt {14} + \sqrt 8 \) \( \ge \) \(\sqrt {50} \)
Đáp án của giáo viên lời giải hay : B
Nếu \(0 < a < b \Rightarrow \sqrt a < \sqrt b \)
Chú ý: Nếu a < b , b < c thì a < c
Ta có:
\(\sqrt {14} < \sqrt {16} = 4;\sqrt 8 < \sqrt 9 = 3\) nên \(\sqrt {14} + \sqrt 8 \) < 4 + 3 = 7
\(\sqrt {50} \) > \(\sqrt {49} = 7\)
Như vậy, \(\sqrt {14} + \sqrt 8 \) < \(\sqrt {50} \)
Có bao nhiêu số thực x thỏa mãn \(\sqrt { - 3x + 2} = 4\)
-
A
0
-
B
1
-
C
2
-
D
4
Đáp án của giáo viên lời giải hay : B
Bình phương cả 2 vế, tìm x
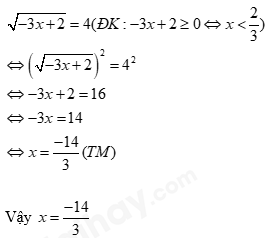
So sánh \(A = \sqrt 7 + \sqrt {15} \) và \(7.\)
-
A
\(A > 7\)
-
B
$A < 7$
-
C
\(A = 7\)
-
D
\(A \ge 7\)
Đáp án của giáo viên lời giải hay : B
Sử dụng cách so sánh hai số dương bất kì \(a\) và \(b\):
+ Nếu \(a = b\) thì \(\sqrt a = \sqrt b \) .
+ Nếu \(a > b\) thì \(\sqrt a > \sqrt b \) .
+ Nếu \(a < b\) thì \(\sqrt a < \sqrt b .\)
Vì \(7 < 9\) nên \(\sqrt 7 < \sqrt 9 \) hay \(\sqrt 7 < 3\) (1)
Vì \(15 < 16\) nên \(\sqrt {15} < \sqrt {16} \) hay \(\sqrt {15} < 4\) (2)
Từ (1) và (2) suy ra \(A = \sqrt 7 + \sqrt {15} < 3 + 4\) hay \(A < 7.\)
Có bao nhiêu giá trị của \(x\) thỏa mãn \(\sqrt {2x + 3} = 25\)
-
A
\(0\)
-
B
$1$
-
C
\(2\)
-
D
\(311\)
Đáp án của giáo viên lời giải hay : B
Sử dụng \(\sqrt x = a\,\left( {a \ge 0} \right)\) thì \(x = {a^2}\).
Ta có \(\sqrt {2x + 3} = 25\)\( \Rightarrow 2x + 3 = {25^2} \Rightarrow 2x + 3 = 625\)
\( \Rightarrow 2x = 625 - 3\) \( \Rightarrow 2x = 622 \Rightarrow x = 311\)
Vậy có một giá trị của \(x\) thỏa mãn là \(x = 311.\)
Tìm \(x\) thỏa mãn \(\sqrt {2x} = 6\).
-
A
\(x = \pm 18\)
-
B
$x = 19$
-
C
\(x = 18\)
-
D
\(x = 36\)
Đáp án của giáo viên lời giải hay : C
Sử dụng \(\sqrt x = a\,\left( {a \ge 0} \right)\) thì \(x = {a^2}\).
Ta có \(\sqrt {2x} = 6\)\( \Rightarrow 2x = {6^2} \Rightarrow 2x = 36\) \( \Rightarrow x = 18.\)
Vậy \(x = 18.\)
Tìm \(x \in \mathbb{Q}\) biết \({x^2} = 225\).
-
A
\(x = 15\)
-
B
$x = - 15$
-
C
\(x = 15\) hoặc \(x = - 15\)
-
D
\(x = 25\)
Đáp án của giáo viên lời giải hay : C
Đưa hai vế về hai lũy thừa cùng số mũ rồi xét các trường hợp có thể xảy ra của cơ số.
Ta có \({x^2} = 225\)\( \Rightarrow {x^2} = {15^2}\)
Suy ra \(x = 15\) hoặc \(x = - 15.\)
Một bạn học sinh làm như sau $5\mathop = \limits_{\left( 1 \right)} \sqrt {25} \mathop = \limits_{\left( 2 \right)} \sqrt {16 + 9} \mathop = \limits_{\left( 3 \right)} \sqrt {16} + \sqrt 9 \mathop = \limits_{\left( 4 \right)} 4 + 3\mathop = \limits_{\left( 5 \right)} 7$ . Chọn kết luận đúng.
-
A
Bạn đã làm đúng.
-
B
Bạn đã làm sai từ bước \(\left( 1 \right)\).
-
C
Bạn đã làm sai từ bước \(\left( 2 \right)\).
-
D
Bạn đã làm sai từ bước \(\left( 3 \right)\).
Đáp án của giáo viên lời giải hay : D
Ta không có tính chất sau: \(\sqrt {A + B} = \sqrt A + \sqrt B \)
Vì \(\sqrt {16 + 9} < \sqrt {16} + \sqrt 9 \,\left( {{\rm{do }}\sqrt {25} = 5 < 7} \right)\) nên bạn đã làm sai từ bước (3).
So sánh hai số \(\sqrt {9.16} \) và \(\sqrt 9 .\sqrt {16} \)
-
A
\(\sqrt {9.16} = \sqrt 9 .\sqrt {16} \)
-
B
\(\sqrt {9.16} < \sqrt 9 .\sqrt {16} \)
-
C
\(\sqrt {9.16} > \sqrt 9 .\sqrt {16} \)
-
D
Không thể so sánh
Đáp án của giáo viên lời giải hay : A
Tính giá trị các căn bậc hai rồi so sánh.
Ta có \(\sqrt {9.16} = \sqrt {144} = 12\) và \(\sqrt 9 .\sqrt {16} = 3.4 = 12\)
Nên \(\sqrt {9.16} = \sqrt 9 .\sqrt {16} \)
Chọn câu đúng.
-
A
\( - \sqrt {\dfrac{{64}}{{121}}} = \dfrac{8}{{11}}\)
-
B
$ - \sqrt {\dfrac{{64}}{{121}}} = - \dfrac{8}{{11}}$
-
C
\( - \sqrt {\dfrac{{64}}{{121}}} = \pm \dfrac{8}{{11}}\)
-
D
\( - \sqrt {\dfrac{{64}}{{121}}} = \dfrac{{ - 32}}{{11}}\)
Đáp án của giáo viên lời giải hay : B
Sử dụng định nghĩa căn bậc hai.
Căn bậc hai của một số $a$ không âm là số $x$ sao cho \({x^2} = a.\)
Với \(\sqrt a \) ta có \(a \ge 0\) và \(\sqrt a \ge 0\).
Vì \(\dfrac{{64}}{{121}} = {\left( {\dfrac{8}{{11}}} \right)^2}\) nên $ - \sqrt {\dfrac{{64}}{{121}}} = - \dfrac{8}{{11}}$
Tính \(\sqrt {49} \)
-
A
\( - 7\)
-
B
\(9\)
-
C
\( \pm 7\)
-
D
\(7\)
Đáp án của giáo viên lời giải hay : D
Sử dụng định nghĩa căn bậc hai.
Căn bậc hai của một số $a$ không âm là số $x$ sao cho \({x^2} = a.\)
Với \(\sqrt a \) ta có \(a \ge 0\) và \(\sqrt a \ge 0\).
Vì \({7^2} = 49\) nên $\sqrt {49} = 7.$
