Hai đường thẳng zz’ và tt’ cắt nhau tại \(A\). Góc đối đỉnh với \(\widehat {zAt'}\) là:
-
A
\(\widehat {z'At'}\)
-
B
\(\widehat {z'At}\)
-
C
\(\widehat {zAt'}\)
-
D
\(\widehat {zAt}\)
Đáp án của giáo viên lời giải hay : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia Az và At, từ đó xác định góc đối đỉnh với \(\widehat {zAt}\).
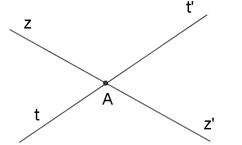
Vì hai đường thẳng \(zz'\) và \(tt'\) cắt nhau tại \(A\) nên \(Az'\) là tia đối của tia \(Az,At'\) là tia đối của tia \(At.\) Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat {xOy} = 135^\circ \) . Chọn câu đúng:
-
A
\(\widehat {x'Oy} = 135^\circ \)
-
B
\(\widehat {x'Oy'} = 45^\circ \)
-
C
\(\widehat {xOy'} = 135^\circ \)
-
D
\(\widehat {x'Oy'} = 135^\circ \)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
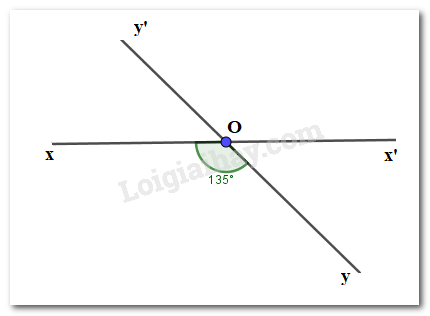
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 135^\circ = 45^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 135^\circ = 45^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 135^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 45^\circ .\)
Cho 2 đường thẳng ab và cd cắt nhau tại M ( tia Ma đối tia Mc). Biết \(\widehat {aMc} = 5.\widehat {bMc}\). Tính số đo \(\widehat {aMc}\) ?
-
A
30\(^\circ \)
-
B
36\(^\circ \)
-
C
144\(^\circ \)
-
D
150\(^\circ \)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
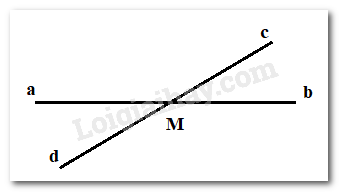
Ta có : \(\widehat {aMc} + \widehat {bMc} = 180^\circ \) ( 2 góc kề bù)
Mà \(\widehat {aMc} = 5.\widehat {bMc}\)
\(\begin{array}{l} \Rightarrow 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ \Rightarrow 6.\widehat {bMc} = 180^\circ \\ \Rightarrow \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \Rightarrow \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
\(\begin{array}{l} \Rightarrow 5.\widehat {bMc} + \widehat {bMc} = 180^\circ \\ \Rightarrow 6.\widehat {bMc} = 180^\circ \\ \Rightarrow \widehat {bMc} = 180^\circ :6 = 30^\circ \\ \Rightarrow \widehat {aMc} = 5.30^\circ = 150^\circ \end{array}\)
Cho \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\); \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
-
A
124o
-
B
142o
-
C
65o
-
D
56o
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)
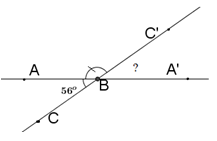
Vì góc \(ABC'\) kề bù với góc \(ABC\) nên \(BC'\) là tia đối của tia \(BC.\)
Vì góc \(C'BA'\) kề bù với góc \(ABC'\) nên \(BA'\) là tia đối của tia \(BA.\)
Do đó, góc \(C'BA'\) và góc \(ABC\) đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
Vẽ góc \(xOy\) có số đo bằng 125o. Vẽ góc \(x'Oy'\) đối đỉnh với góc \(xOy.\) Viết tên các góc có số đo bằng 55o.
-
A
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
-
B
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
-
C
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
-
D
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
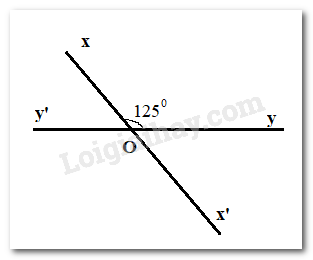
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox;Oy'\) là tia đối của tia \(Oy.\)
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 125^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên
\(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\( \Rightarrow 125^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 125^\circ = 55^\circ \)
Hai góc có số đo bằng 55o là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Cho tia Ok là tia phân giác của \(\widehat {mOn}\)= 70o . Tính \(\widehat {nOk}\)
-
A
70o
-
B
140o
-
C
35o
-
D
110o
Đáp án của giáo viên lời giải hay : C
Sử dụng tính chất tia phân giác của một góc
Vì Ok là tia phân giác của \(\widehat {mOn}\) nên \(\widehat {mOk} = \widehat {nOk} = \frac{1}{2}.\widehat {mOn} = \frac{1}{2}.70^\circ = 35^\circ \)
Hai đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(O\), tạo thành \(\widehat {MOP} = 50^\circ \) . Cho tia OK là tia phân giác của \(\widehat {PON}\). Chọn khẳng định sai.
-
A
\(\widehat {MOQ} = \widehat {PON} = {130^o}\)
-
B
\(\widehat {POK} = \widehat {NOK} = 50^\circ \)
-
C
\(\widehat {MOQ} + \widehat {QON} = {180^o}\)
-
D
\(\widehat {QON} = 50^\circ \)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc
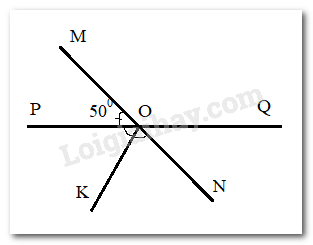
Ta có : \(\widehat {QON} = \widehat {MOP} = 50^\circ \) ( 2 góc đối đỉnh)
\(\widehat {MOQ} + \widehat {QON} = {180^o}\) ( 2 góc kề bù)
\(\widehat {MOP} + \widehat {PON} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 50^\circ + \widehat {PON} = 180^\circ \\ \Rightarrow \widehat {PON} = 180^\circ - 50^\circ = 130^\circ \end{array}\)
Vì OK là tia phân giác của \(\widehat {PON}\)
\( \Rightarrow \widehat {POK} = \widehat {NOK} = \frac{1}{2}.\widehat {PON} = \frac{1}{2}.130^\circ = 65^\circ \)
Vậy khẳng định A, C, D đúng, B sai
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {70^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
-
A
\(\widehat {yOt'} = {35^o}\)
-
B
\(\widehat {yOt'} = {70^o}\)
-
C
\(\widehat {yOt'} = {145^o}\)
-
D
\(\widehat {yOt'} = {110^o}\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng tính chất tia phân giác của một góc
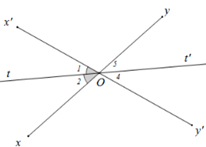
Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên \(\widehat {xOt} = \widehat {tOx'} = \frac{1}{2}\widehat {xOx'} = \frac{1}{2}{.70^o} = {35^o}\)
Vì \(Oy\) là tia đối của \(Ox,Ot'\) là tia đối của \(Ot\)
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Cho \(\widehat {xOy},\widehat {yOz}\) là 2 góc kề bù. Góc xOy có số đo là 60o . Kẻ Om và On lần lượt là tia phân giác của 2 góc đó. Tính số đo góc mOn
-
A
30o
-
B
60o
-
C
120o
-
D
90o
Đáp án của giáo viên lời giải hay : D
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất tia phân giác của một góc
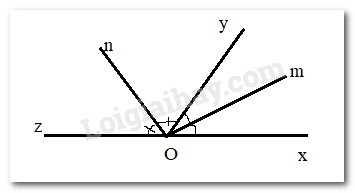
Ta có: \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) ( 2 góc kề bù)
\(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì Om là tia phân giác của góc xOy nên \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì On là tia phân giác của góc yOz nên \(\widehat {yOn} = \widehat {nOz} = \frac{1}{2}.\widehat {yOz} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oy nằm giữa 2 tia Om và On nên \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\). Biết \(\widehat {AOD} - \widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
-
A
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
-
B
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
-
C
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
-
D
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án của giáo viên lời giải hay : B
+ Tính số đo góc AOC nhờ bài toán biết tổng và hiệu.
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
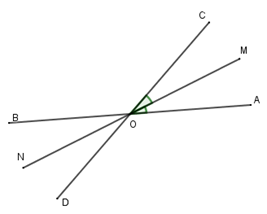
Ta có: \(\widehat {mOn} = \widehat {mOy} + \widehat {yOn} = 30^\circ + 60^\circ = 90^\circ \) ( 2 góc kề bù)
Mà \(\widehat {AOD} - \widehat {AOC} = 60^\circ \)
\( \Rightarrow \widehat {AOC} = \left( {180^\circ - 60^\circ } \right):2 = 60^\circ \)
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \frac{{\widehat {COA}}}{2} = \frac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
-
A
\(\widehat {z'At'}\)
-
B
\(\widehat {z'At}\)
-
C
\(\widehat {zAt'}\) \(\)
-
D
\(\widehat {zAt}\)
Đáp án của giáo viên lời giải hay : B
Áp dụng định nghĩa hai góc đối đỉnh, xác định tia đối của tia \(Az\) và \(At'\), từ đó xác định góc đối đỉnh với \(\widehat {zAt'}\).
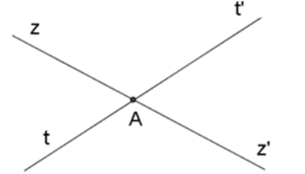
Vì hai đường thẳng $zz'$ và $tt'$ cắt nhau tại $A$ nên $Az'$ là tia đối của tia $Az,At'$ là tia đối của tia $At.$ Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
-
A
$30^\circ$
-
B
$120^\circ$
-
C
$90^\circ$
-
D
$60^\circ$
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
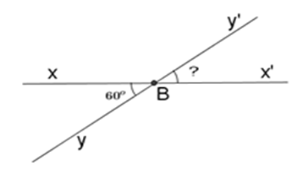
Vẽ \(\widehat {x'By'}\) là góc đối đỉnh với \(\widehat {xBy}\). Khi đó:
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\) (tính chất hai góc đối đỉnh)
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
-
A
$\widehat {x'Oy} = 135^\circ $
-
B
$\widehat {x'Oy'} = 45^\circ $
-
C
$\widehat {xOy'} = 135^\circ $
-
D
$\widehat {x'Oy'} = 135^\circ $
Đáp án của giáo viên lời giải hay : D
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
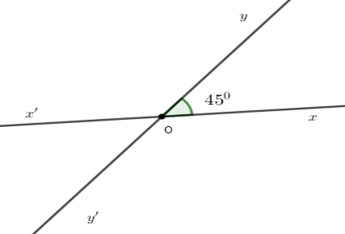
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
-
A
\(\widehat {zOt} = \widehat {z'Ot'} = 72^\circ \)
-
B
\(\widehat {zOt} = \widehat {z'Ot'} = 30^\circ \)
-
C
\(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ \)
-
D
\(\widehat {zOt} = 72^\circ ;\,\widehat {z'Ot'} = 36^\circ \)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
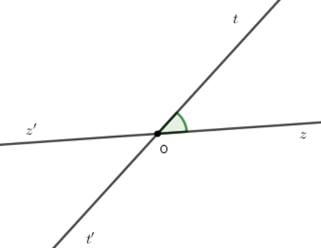
Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) mà \(\widehat {tOz'} = 4.\widehat {tOz}\) \( \Rightarrow \widehat {zOt} + 4.\widehat {zOt} = 180^\circ \) \( \Rightarrow 5.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)
Vẽ \(\widehat {ABC} = {56^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
-
A
$124^\circ$
-
B
$142^\circ$
-
C
$65^\circ$
-
D
$56^\circ$
Đáp án của giáo viên lời giải hay : D
Áp dụng tính chất hai góc kề bù, xác định các tia đối từ đó xác định góc đối đỉnh. Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'.\)
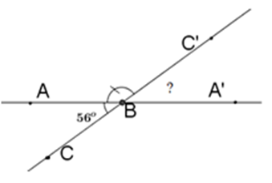
Vì góc \(ABC'\) kề bù với góc $ABC$ nên $BC'$ là tia đối của tia $BC.$
Vì góc $C'BA'$ kề bù với góc $ABC'$ nên $BA'$ là tia đối của tia $BA.$
Do đó, góc $C'BA'$ và góc $ABC$ đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {ABC} = {56^o}\)
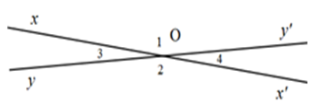
Cho hình vẽ sau. Biết góc $xOy'$ đối đỉnh với góc $x'Oy,$ biết \(\widehat {xOy'} = {\widehat O_1} = {165^o}\). Tính các góc đỉnh O (khác góc bẹt).
-
A
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
-
B
\({\widehat O_2} = {165^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {15^o}\,\,\)
-
C
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {15^o};\,\,{\widehat O_4} = {165^o}\,\,\)
-
D
\({\widehat O_2} = {15^o};\,{\widehat O_3} = {165^o};\,\,{\widehat O_4} = {15^o}\,\,\)
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất hai góc đối đỉnh, hai góc kề bù để tính các góc còn lại.
\({\widehat O_2} = {\widehat O_1} = {165^o}\) (tính chất hai góc đối đỉnh)
Góc ${O_1}$ và góc ${O_4}$ là hai góc kề bù
\( \Rightarrow {\widehat O_1} + {\widehat O_4} = {180^o}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {\widehat O_1}\)
\( \Rightarrow {\widehat O_4} = {180^o} - {165^o} = {15^o}\)
\({\widehat O_3} = {\widehat O_4} = {15^o}\,\) (hai góc đối đỉnh)
Vẽ góc $xOy$ có số đo bằng $35^\circ$. Vẽ góc $x'Oy'$ đối đỉnh với góc $xOy.$ Viết tên các góc có số đo bằng $145^o.$
-
A
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy'}\)
-
B
\(\widehat {xOy}\,\,;\,\,\widehat {x'Oy'}\)
-
C
\(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
-
D
\(\widehat {xOy'}\,\,;\,\,\widehat {xOy}\)
Đáp án của giáo viên lời giải hay : C
Áp dụng tính chất hai góc đối đỉnh, tính chất hai góc kề bù để tính các góc còn lại.
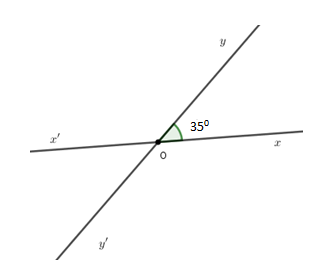
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 35^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 35^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 35^\circ \)
\( \Rightarrow \widehat {x'Oy} = 145^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 145^\circ .\)
Hai góc có số đo bằng ${145^o}$ là : \(\widehat {xOy'}\,\,;\,\,\widehat {x'Oy}\)
Hai đường thẳng $xy$ và $x'y'$ cắt nhau tại $O.$ Biết \(\widehat {xOx'} = {70^o}\). $Ot$ là tia phân giác của góc xOx’. $Ot'$ là tia đối của tia $Ot.$ Tính số đo góc $yOt'.$
-
A
\(\widehat {yOt'} = {35^o}\)
-
B
\(\widehat {yOt'} = {70^o}\)
-
C
\(\widehat {yOt'} = {145^o}\)
-
D
\(\widehat {yOt'} = {110^o}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng tính chất tia phân giác của một góc. Áp dụng tính chất hai góc đối đỉnh để tính số đo góc $yOt'.$
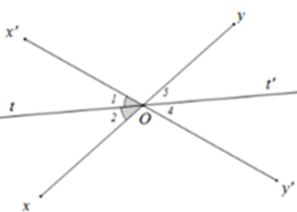
Vì $Ot$ là tia phân giác của góc $xOx'$ nên
\(\widehat {xOt} = \widehat {tOx'} = \dfrac{1}{2}\widehat {xOx'} = \dfrac{1}{2}{.70^o} = {35^o}\)
Vì $Oy$ là tia đối của $Ox,Ot'$ là tia đối của $Ot$
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {35^o}\) (tính chất hai góc đối đỉnh).
Hai đường thẳng $MN$ và $PQ$ cắt nhau tại $O$, tạo thành góc $MOP$ có số đo bằng ${80^o}.$
Chọn câu đúng.
-
A
$\widehat {MOQ} = \widehat {PON} = {100^o}$
-
B
$\widehat {MOQ} = \widehat {PON} = {80^o}$
-
C
$\widehat {MOQ} + \widehat {PON} = {180^o}$
-
D
$\widehat {MOQ} = \widehat {PON} = {160^o}$
Đáp án của giáo viên lời giải hay : A
Áp dụng tính chất $2$ góc đối đỉnh, tính chất $2$ góc kề bù. Tính các góc còn lại.
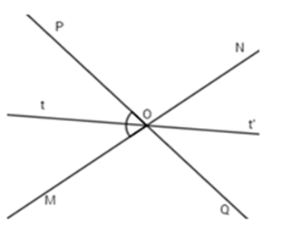
$\widehat {NOQ} = \widehat {MOP} = {80^o}$ (tính chất hai góc đối đỉnh)
Vì góc $MOP$ và $PON$ là hai góc kề bù nên :
$\,\widehat {MOP} + \widehat {PON} = {180^o} \Rightarrow {80^o} + \widehat {PON} = {180^o}$ $ \Rightarrow \widehat {PON} = {180^o} - {80^o} = {100^o}$
Khi đó $\widehat {MOQ} = \widehat {PON} = {100^o}$ (tính chất hai góc đối đỉnh).
Vẽ tia $Ot$ là tia phân giác của góc $MOP,$ $Ot'$ là tia đối của tia $Ot.$ Chọn câu đúng.
-
A
$Ot'$ là tia phân giác của góc $NOP.$
-
B
$Ot'$ là tia phân giác của góc $NOQ.$
-
C
$ON$ là tia phân giác của góc $t'OP.$
-
D
Cả A, B, C đều sai.
Đáp án của giáo viên lời giải hay : B
Áp dụng tính chất tia phân giác của một góc để tính $2$ góc $MOt,POt.$ Xác định tia đối, áp dụng tính chất hai góc đối đỉnh, tính $2$ góc $NOt',QOt'.$ Từ đó chứng minh $Ot'$ là tia phân giác của góc $NOQ.$
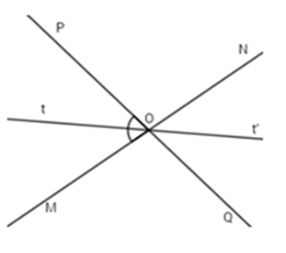
Vì $Ot$ là tia phân giác của góc $MOP$ nên $\widehat {MOt} = \widehat {tOP} = \dfrac{1}{2}\widehat {MOP} = \dfrac{1}{2}{.80^o} = {40^o}.$
Vì $Ot'$ là tia đối của tia $Ot,$ do đó :
\(\widehat {NOt'} = \widehat {MOt} = {40^o}\,\,\,\) (hai góc đối đỉnh)
\(\widehat {t'OQ} = \widehat {tOP} = {40^o}\,\,\,\,\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {NOt'} = \widehat {t'OQ}\)
Mặt khác tia $Ot'$ nằm trong góc $NOQ.$ Vậy $Ot'$ là tia phân giác của góc $NOQ.$
Cho đường thẳng $AB$ và điểm $O$ trên đường thẳng đó. Trên cùng một nửa mặt phẳng bờ $AB$ vẽ hai tia $OC$ và $OD$ sao cho \(\widehat {AOC} = \widehat {BOD} = {50^o}\). Trên nửa mặt phẳng bờ $AB$ không chứa tia $OD,$ vẽ tia $OE$ sao cho tia $OA$ là tia phân giác của góc $COE.$ Chọn câu đúng?
-
A
$\widehat {AOC};\widehat {BOD}$ là hai góc đối đỉnh
-
B
$OD$ và \(OE\) là hai tia đối nhau
-
C
Hai góc $BOD$ và $AOE$ là hai góc đối đỉnh
-
D
Cả B, C đều đúng.
Đáp án của giáo viên lời giải hay : D
+ Xác định các tia đối, áp dụng định nghĩa hai góc đối đỉnh.
+ Áp dụng tính chất tia phân giác của một góc, tính góc $AOE.$ Áp dụng tính chất tia phân giác của một góc, tính tổng hai góc, chứng minh góc kề bù, từ đó xác định tia đối, hai góc đối đỉnh.
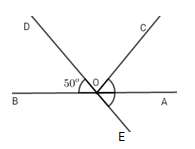
+ Hai góc $AOC$ và $BOD$ có: $OA$ và $OB$ là hai tia đối nhau, $OD$ và $OC$ không phải là hai tia đối nhau.
Vậy hai góc đó không phải là hai góc đối đỉnh.
+ Vì góc $BOD$ và $DOA$ là hai góc kề bù nên:
$\begin{array}{l}\,\,\,\,\,\widehat {BOD} + \widehat {DOA} = {180^O}\\ \Rightarrow {50^O} + \widehat {DOA} = {180^O}\\ \Rightarrow \widehat {DOA} = {180^O} - {50^O} = {130^O}\end{array}$
Tia $OA$ là tia phân giác góc $COE$ nên \(\widehat {AOE} = \widehat {AOC} = {50^O}\).
Tia $OD$ và tia $OE$ thuộc hai nửa mặt phẳng đối nhau bờ chứa tia $OA$ nên tia $OA$ nằm giữa hai tia $OD$ và $OE,$ ta có:
\(\widehat {DOA} + \widehat {AOE} = {130^0} + {50^0} = {180^0}\)
Suy ra $OD$ và $OE$ là hai tia đối nhau.
Hai góc $BOD$ và $AOE$ có hai cặp cạnh $OB$ và $OA,OD$ và $OE$ là hai tia đối nhau nên là hai góc đối đỉnh.
Cho \(\widehat {AOB} = 50^\circ \) , tia \(OC\) là tia phân giác của \(\widehat {AOB}\). Gọi \(OD\) là tia đối của tia \(OC\). Trên nửa mặt phẳng bờ \(CD\) chứa tia \(OA\), vẽ tia \(OE\) sao cho \(\widehat {DOE} = 25^\circ \). Góc nào dưới đây đối đỉnh với \(\widehat {DOE}\).
-
A
$\widehat {DOA}$
-
B
$\widehat {COA}$
-
C
$\widehat {AOE}$
-
D
$\widehat {BOC}$
Đáp án của giáo viên lời giải hay : D
+ Chứng minh \(OB\) và \(OE\) là hai tia đối nhau.
+ Từ đó suy ra cặp góc đối đỉnh theo định nghĩa.
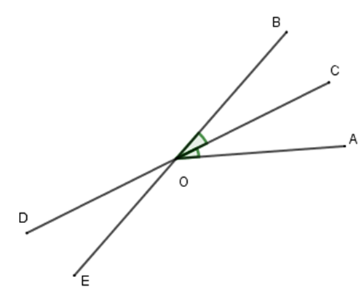
Vì \(OC\) và \(OD\) là hai tia đối nhau nên \(\widehat {COE}\) và \(\widehat {DOE}\) là hai góc kề bù. Khi đó \(\widehat {COE} + \widehat {DOE} = 180^\circ \)\( \Rightarrow \widehat {COE} = 180^\circ - 25^\circ = 155^\circ \)
Vì \(OC\) là tia phân giác của góc \(BOA\) nên \(\widehat {COB} = \dfrac{{\widehat {AOB}}}{2} = \dfrac{{50^\circ }}{2} = 25^\circ \)
Nhận thấy \(\widehat {BOC} + \widehat {COE} = 25^\circ + 155^\circ = 180^\circ \) nên \(OB\) và \(OE\) là hai tia đối nhau.
Suy ra \(\widehat {BOC}\) và \(\widehat {DOE}\) là hai góc đối đỉnh.
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại $O$ tạo thành \(\widehat {AOC} = 60^\circ \) . Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
-
A
\(\widehat {BON} = \widehat {DON} = 25^\circ \)
-
B
\(\widehat {BON} = \widehat {DON} = 30^\circ \)
-
C
\(\widehat {BON} = \widehat {DON} = 60^\circ \)
-
D
\(\widehat {BON} = \widehat {DON} = 45^\circ \)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng tính chất tia phân giác tính các góc \(\widehat {AOM};\widehat {COM}\)
+ Sử dụng tính chất hai góc đối đỉnh để suy ra hai góc \(\widehat {BON}\) và \(\widehat {DON}.\)
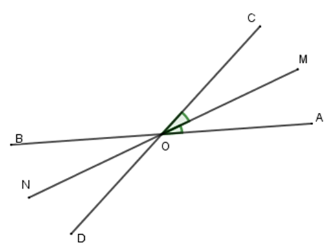
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OA\) và \(OB\) là hai tia đối nhau, \(OC\) và \(OD\) là hai tia đối nhau.
Vì \(OM\) là tia phân giác \(\widehat {COA}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {COA}}}{2} = \dfrac{{60}}{2} = 30^\circ \)
Mà \(ON\) và \(OM\) là hai tia đối nhau nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh
Suy ra \(\widehat {AOM} = \widehat {BON} = 30^\circ ;\widehat {COM} = \widehat {DON} = 30^\circ \) hay \(\widehat {BON} = \widehat {DON} = 30^\circ .\)
Hai đường thẳng $AB$ và $CD$ cắt nhau tại $O.$ Biết \(\widehat {AOC} - \widehat {AOD} = {50^0}.\) Chọn câu đúng.
-
A
\(\widehat {AOC} = 110^\circ \)
-
B
\(\widehat {BOC} = 65^\circ \)
-
C
\(\widehat {BOD} = 120^\circ \)
-
D
\(\widehat {AOD} = 50^\circ \)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng: Tổng hai góc kề bù bằng \(180^\circ .\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau
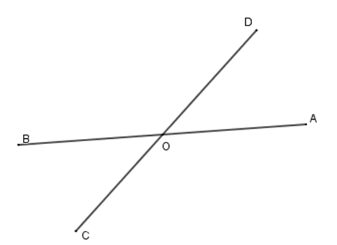
Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} - \widehat {AOD} = 50^\circ \)
Nên \(\widehat {AOC} = \dfrac{{180^\circ + 50^\circ }}{2} = 115^\circ \) và \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 65^\circ \)
Mà \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh nên \(\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Lại có \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh nên \(\widehat {BOD} = \widehat {AOC} = 115^\circ .\)
Vậy \(\widehat {BOD} = \widehat {AOC} = 115^\circ ;\,\widehat {BOC} = \widehat {AOD} = 65^\circ .\)
Chọn phát biểu sai trong các phát biểu sau:
-
A
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì tia \(Ot\) nằm giữa hai tia \(Ox;Oy.\)
-
B
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
-
C
Nếu \(\widehat {xOt} = \widehat {yOt}\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
-
D
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\).
Đáp án của giáo viên lời giải hay : C
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên C sai, D đúng.
Cho $Ot$ là tia phân giác của \(\widehat {xOy}\). Biết \(\widehat {xOy} = {100^0}\), số đo của \(\widehat {xOt}\) là:
-
A
\({40^0}\)
-
B
\({60^0}\)
-
C
\({50^0}\)
-
D
\({200^0}\)
Đáp án của giáo viên lời giải hay : C
Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{100^\circ }}{2} = 50^\circ \)
Cho \(\widehat {xOy}\) là góc vuông có tia On là phân giác, số đo của \(\widehat {xOn}\) là:
-
A
\({40^0}\)
-
B
\({90^0}\)
-
C
\({45^0}\)
-
D
\({85^0}\)
Đáp án của giáo viên lời giải hay : C
+ Góc vuông là góc có số đo bằng \(90^\circ \)
+ Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì \(On\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOn} = \widehat {nOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Cho tia \(On\) là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {70^0}\), số đo của \(\widehat {mOt}\) là:
-
A
\({140^0}\)
-
B
\({120^0}\)
-
C
\({35^0}\)
-
D
\({60^0}\)
Đáp án của giáo viên lời giải hay : A
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(On\) là tia phân giác của \(\widehat {mOt}\) nên \(\widehat {mOn} = \widehat {nOt} = \dfrac{{\widehat {mOt}}}{2}\)
\( \Rightarrow \widehat {mOt} = 2.\widehat {mOn} = 2.70^\circ = 140^\circ \).
Cho \(\widehat {AOB} = 90^\circ \) và tia \(OB\) là tia phân giác của góc \(AOC.\) Khi đó góc \(AOC\) là
-
A
Góc vuông
-
B
Góc nhọn
-
C
Góc tù
-
D
Góc bẹt
Đáp án của giáo viên lời giải hay : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
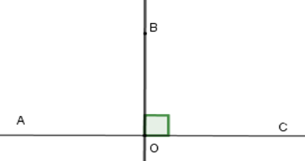
Vì tia \(OB\) là tia phân giác của góc \(AOC\) nên \(\widehat {AOB} = \widehat {BOC} = \dfrac{{\widehat {AOC}}}{2}\)
Do đó \(\widehat {AOC} = 2.\widehat {AOB} = 2.90^\circ = 180^\circ \)
Nên góc \(AOC\) là góc bẹt.
Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
-
A
\(\widehat {AOB} = 70^\circ ;\,\widehat {BOC} = 140^\circ \)
-
B
\(\widehat {AOB} = 90^\circ ;\,\widehat {BOC} = 120^\circ \)
-
C
\(\widehat {AOB} = 120^\circ ;\,\widehat {BOC} = 60^\circ \)
-
D
\(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \)
Đáp án của giáo viên lời giải hay : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
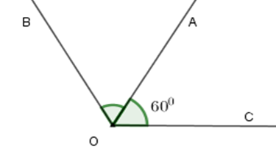
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên ta có
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) nên \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 2.\widehat {AOC} = 2.60^\circ = 120^\circ \)
Vậy \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \).
Cho \(\widehat {AOB} = {110^0}\) và \(\widehat {AOC} = {55^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau. Chọn câu sai.
-
A
Tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\)
-
B
Tia \(OC\) là tia phân giác góc \(AOB.\)
-
C
\(\widehat {BOC} = 65^\circ \)
-
D
\(\widehat {BOC} = 55^\circ \)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng dấu hiệu nhận biết tia nằm giữa hai tia
+ Tính góc \(BOC\)
+ Sử dụng định nghĩa tia phân giác
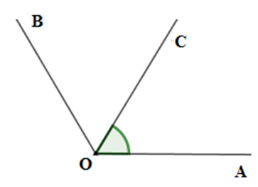
Vì \(\widehat {AOB}\) và \(\widehat {AOC}\) không kề nhau nên hai tia \(OC;OB\) thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia \(OA\). Lại có \(\widehat {AOC} < \widehat {AOB}\,\left( {55^\circ < 110^\circ } \right)\) nên tia \(OC\) nằm giữa hai tia \(OA\) và \(OB.\) (1)
Từ đó \(\widehat {AOC} + \widehat {COB} = \widehat {AOB}\,\) hay \(\widehat {COB} = \widehat {AOB} - \widehat {AOC} = 110^\circ - 55^\circ = 55^\circ \)
Suy ra \(\widehat {AOC} = \widehat {BOC} = 55^\circ \) (2)
Từ (1) và (2) suy ra tia \(OC\) là tia phân giác góc \(AOB.\)
Vậy A, B, D đúng và C sai.
Cho \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 120^\circ \) và tia \(Ot\) là tia phân giác của \(\widehat {yOz}.\) Tính số đo góc \(xOt.\)
-
A
\({140^0}\)
-
B
\({150^0}\)
-
C
\({90^0}\)
-
D
\({120^0}\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng: Hai góc kề bù có tổng số đo bằng \(180^\circ \) và tính chất tia phân giác của một góc để tính toán.
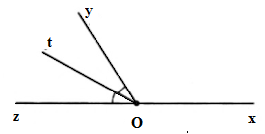
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \).
Lại có tia \(Ot\) là tia phân giác của \(\widehat {yOz}\) nên \(\widehat {zOt} = \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}.60^\circ = 30^\circ \)
Lại có \(\widehat {zOt};\,\widehat {tOx}\) là hai góc kề bù nên \(\widehat {zOt} + \widehat {tOx} = 180^\circ \Rightarrow \widehat {tOx} = 180^\circ - \widehat {zOt}\)\( = 180^\circ - 30^\circ = 150^\circ .\)
Vậy \(\widehat {tOx} = 150^\circ .\)
Cho góc \(AOB\) và tia phân giác \(OC\) của góc đó. Vẽ tia phân giác \(OM\) của góc \(BOC.\) Biết \(\widehat {BOM} = 35^\circ .\) Tính số đo góc \(AOB.\)
-
A
\({150^0}\)
-
B
\({120^0}\)
-
C
\({140^0}\)
-
D
\({160^0}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng: Nếu tia \(Ot\) là tiam phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
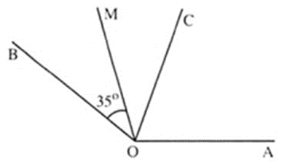
Vì tia \(OM\) là tia phân của góc \(BOC\)
nên \(\widehat {BOC} = 2.\widehat {BOM} = 2.35^\circ = 70^\circ \)
Lại có tia \(OC\) là tia phân giác của \(\widehat {AOB}\) nên \(\widehat {AOB} = 2.\widehat {BOC} = 2.70^\circ = 140^\circ \). Vậy \(\widehat {AOB} = 140^\circ \).
Cho góc bẹt \(xOy\). Trên cùng một nửa mặt phẳng bờ \(xy\) vẽ các tia \(Om;On\) sao cho \(\widehat {xOm} = a^\circ \,\left( {a < 180} \right)\) và \(\widehat {yOn} = 70^\circ .\) Với giá trị nào của \(a\) thì tia \(On\) là tia phân giác của \(\widehat {yOm}\).
-
A
\({45^0}\)
-
B
\({30^0}\)
-
C
\({50^0}\)
-
D
\({40^0}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng tính chất tia phân giác và tính chất hai góc kề bù.
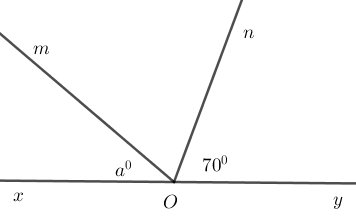
Giả sử tia \(On\) là tia phân giác của góc \(yOm\) thì \(\widehat {mOy} = 2.\widehat {yOn} = 2.70^\circ = 140^\circ \).
Mà hai góc \(\widehat {xOm};\widehat {yOm}\) là hai góc kề bù nên \(\widehat {xOm} + \widehat {yOm} = 180^\circ \)\( \Rightarrow \widehat {xOm} = 180^\circ - \widehat {yOm}\) \( = 180^\circ - 140^\circ = 40^\circ \).
Vậy \(a = 40 ^\circ\).
Cho hai góc kề bù \(\widehat {AOB};\,\widehat {BOC}\). Vẽ tia phân giác \(OM\) của góc \(BOA\) . Biết số đo góc \(MOC\) gấp \(5\) lần số đo góc \(AOM\). Tính số đo góc \(BOC\).
-
A
\({120^0}\)
-
B
\({130^0}\)
-
C
\({60^0}\)
-
D
\({90^0}\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng tính chất hai góc kề bù và tính chất tia phân giác của một góc để tính toán
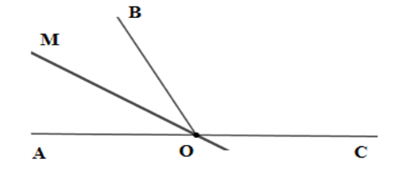
Vì hai góc kề bù \(\widehat {AOB};\,\widehat {BOC}\) nên \(\widehat {AOC} = 180^\circ \) hay \(OA;OC\) là hai tia đối nhau.
Suy ra hai góc \(\widehat {MOC};\widehat {MOA}\) là hai góc kề bù nên \(\widehat {MOA} + \widehat {MOC} = 180^\circ \) mà \(\widehat {MOC} = 5.\widehat {MOA}\) (gt)
Nên \(\widehat {MOA} + 5.\widehat {MOA} = 180^\circ \Rightarrow 6.\widehat {MOA} = 180^\circ \) suy ra \(\widehat {MOA} = 180^\circ :6 = 30^\circ \)
Mà tia phân giác \(OM\) của góc \(BOA\) nên \(\widehat {BOA} = 2.\widehat {MOA} = 2.30^\circ = 60^\circ \)
Lại có hai góc kề bù \(\widehat {AOB};\,\widehat {BOC}\) nên \(\widehat {AOB} + \,\widehat {BOC} = 180^\circ \) suy ra \(\widehat {BOC} = 180^\circ - \widehat {AOB} = 180^\circ - 60^\circ = 120^\circ \)
Vậy \(\widehat {BOC} = 120^\circ \).
Cho hai góc kề bù \(\widehat {xOy};\,\widehat {xOz}\). Vẽ tia \(Ot\) là phân giác \(\widehat {xOy}\) và tia \(Ot'\) là phân giác \(\widehat {xOz}\). Tính \(\widehat {tOt'}\).
-
A
\({70^0}\)
-
B
\({80^0}\)
-
C
\({60^0}\)
-
D
\({90^0}\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng tính chất hai góc kề bù và tính chất tia phân giác của một góc để tính toán
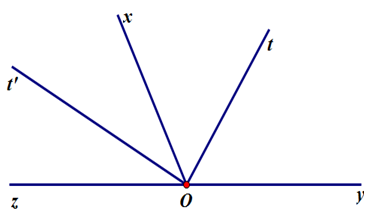
Vì tia \(Ot\) là phân giác \(\widehat {xOy}\) nên \(\widehat {yOt} = \widehat {xOt} = \dfrac{1}{2}\widehat {xOy}\) suy ra \(\widehat {xOy} = 2.\widehat {tOx}\) (1)
Và tia \(Ot'\) là phân giác \(\widehat {yOz}\) nên \(\widehat {zOt'} = \widehat {xOt'} = \dfrac{1}{2}\widehat {xOz}\) suy ra \(\widehat {xOz} = 2.\widehat {t'Ox}\) (2)
Mà \(\widehat {xOy};\,\widehat {xOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOz} = 180^\circ \) (3)
Từ (1) (2) (3) suy ra \(2.\widehat {tOx} + 2.\widehat {t'Ox} = 180^\circ \) suy ra \(2.\left( {\widehat {tOx} + \widehat {t'Ox}} \right) = 180^\circ \Rightarrow \widehat {tOx} + \widehat {t'Ox} = 90^\circ \) (4)
Lại có tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) và tia \(Ot'\) nằm giữa hai tia \(Ox;Oz\) nên tia \(Ox\) nằm giữa hai tia \(Ot;Ot'.\)
Do đó \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'}\) (5)
Từ (4) (5) suy ra \(\widehat {tOx} + \widehat {t'Ox} = \widehat {tOt'} = 90^\circ \).
Cho \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau. Biết \(\widehat {AOB} = \widehat {AOC} = {65^0}\),
Chọn câu đúng.
-
A
Tia \(OB\) là tia phân giác của \(\widehat {AOC}\).
-
B
Tia \(OC\) là tia phân giác của \(\widehat {BOA}\).
-
C
Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
-
D
Không có tia nào là tia phân giác của góc.
Đáp án của giáo viên lời giải hay : C
Sử dụng định nghĩa tia phân giác của một góc
Nếu \(\widehat {xOt} = \widehat {yOt}\) và tia \(Ot\) nằm giữa hai tia \(Ox;Oy\) thì tia $Ot$ là tia phân giác của \(\widehat {xOy}\).
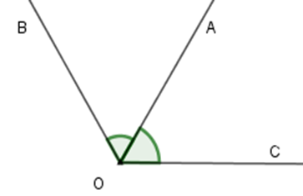
Vì \(\widehat {AOB},\;\widehat {AOC}\) kề với nhau nên tia \(OA\) nằm giữa hai tia \(OB;OC\) mà \(\widehat {AOB} = \widehat {AOC} = {65^0}\) nên tia Tia \(OA\) là tia phân giác của \(\widehat {BOC}\).
Số đo góc \(BOC\) là
-
A
\({140^0}\)
-
B
\({120^0}\)
-
C
\({35^0}\)
-
D
\({130^0}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) (theo câu trước) nên
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) hay \(\widehat {BOC} = 2.\widehat {AOC} = 2.65^\circ = 130^\circ \).
Cho hai góc kề bù \(\widehat {xOy}\) và \(\widehat {yOz}\) sao cho \(\widehat {xOy} = {120^0}\). Gọi Ot là tia phân giác của \(\widehat {xOy}\), vẽ tia Om trong góc \(\widehat {yOz}\) sao cho \(\widehat {tOm} = {90^0}\).
Tính \(\widehat {yOm}\).
-
A
\({30^0}\)
-
B
\({40^0}\)
-
C
\({35^0}\)
-
D
\({60^0}\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng tính chất tia phân giác để tính \(\widehat {tOy}\)
+ Sử dụng tính chất cộng góc để tính \(\widehat {yOz}\).

Vì $Ot$ là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {tOy} = \dfrac{{\widehat {xOy}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \).
Lại có tia \(Ot\) nằm trong góc \(xOy\) và tia \(Om\) nằm trong góc \(yOz\) mà hai góc \(\widehat {xOy};\,\widehat {yOz}\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Om;Ot\). Do đó \(\widehat {tOy} + \widehat {yOm} = \widehat {tOm}\) hay \(\widehat {yOm} = 90^\circ - \widehat {tOy} = 90^\circ - 60^\circ = 30^\circ \).
Vậy \(\widehat {yOm} = 30^\circ \).
Tia \(Om\) có phải là tia phân giác của \(\widehat {yOz}\) không? Vì sao?
-
A
Tia \(Om\) là tia phân giác của \(\widehat {xOz}\)
-
B
Tia \(Om\) là tia phân giác của \(\widehat {mOz}\)
-
C
Tia \(Om\) là tia phân giác của \(\widehat {tOz}\)
-
D
Tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng tổng hai góc kề bù bằng \(180^\circ \) để tính \(\widehat {yOz}\)
Sử dụng công thức cộng góc để tính \(\widehat {mOz}\)
Sử dụng định nghĩa tia phân giác để kết luận.
+ Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {yOz} = 180^\circ \) mà \(\widehat {xOy} = 120^\circ \) nên \(\widehat {yOz} = 180^\circ - 120^\circ = 60^\circ \)
+ Vì tia \(Om\) nằm trong góc \(\widehat {yOz}\) nên tia \(Om\) nằm giữa hai tia \(Oy;Oz\) (1)
Do đó \(\widehat {yOm} + \widehat {mOz} = \widehat {yOz}\) suy ra \(\widehat {mOz} = \widehat {yOz} - \widehat {yOm} = 60^\circ - 30^\circ = 30^\circ \)
Hay \(\widehat {mOz} = \widehat {yOm} = 30^\circ \) (2)
Từ (1) và (2) suy ra tia \(Om\) là tia phân giác của \(\widehat {yOz}\)
Cho góc \(xOy\) bằng \(110^\circ \) có tia \(Oz\) là tia phân giác. Vẽ các tia \(Om;On\) nằm trong góc \(xOy\) sao cho \(\widehat {xOm} = \widehat {yOn} = 30^\circ \).
Tính góc \(zOn\).
-
A
\({40^0}\)
-
B
\({30^0}\)
-
C
\({25^0}\)
-
D
\({60^0}\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng tính chất tia phân giác để tính \(\widehat {yOz}\)
+ Sử dụng dấu hiệu tia nằm giữa hai tia và tính chất cộng góc để tính \(\widehat {zOn}\)
Vì tia \(Oz\) là tia phân giác của góc \(xOy\) nên \(\widehat {xOz} = \widehat {yOz} = \dfrac{1}{2}\widehat {yOx} = \dfrac{1}{2}.110^\circ = 55^\circ \)
Trên nửa mặt phẳng bờ $Oy$ có \(\widehat {yOn} < \widehat {yOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(On\) nằm giữa hai tia \(Oy;Oz\).
Do đó \(\widehat {yOn} + \widehat {nOz} = \widehat {zOy}\) \( \Rightarrow \widehat {zOn} = \widehat {zOy} - \widehat {yOn} = 55^\circ - 30^\circ = 25^\circ \).
Chọn câu đúng.
-
A
Tia \(Oz\) là tia phân giác của \(\widehat {xOn}\).
-
B
Tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
-
C
Tia \(Oz\) là tia phân giác của \(\widehat {mOy}\).
-
D
Tia \(Oz\) là tia phân giác của \(\widehat {xOz}\).
Đáp án của giáo viên lời giải hay : B
Tính góc \(mOz\) từ đó sử dụng định nghĩa để suy ra tia phân giác của một góc.
Trên nửa mặt phẳng bờ $Oy$, vì \(\widehat {xOz} = 55^\circ \) (theo câu trước) nên \(\widehat {xOm} < \widehat {xOz}\,\left( {30^\circ < 55^\circ } \right)\) nên tia \(Om\) nằm giữa hai tia \(Ox;Oz\)
Do đó \(\widehat {xOm} + \widehat {mOz} = \widehat {xOz} \Rightarrow \widehat {mOz} = 55^\circ - 30^\circ = 25^\circ \)
Suy ra \(\widehat {mOz} = \widehat {nOz} = 25^\circ \) (1)
Vì \(On\) nằm giữa hai tia \(Oy;Oz\) (theo câu trước) và tia \(Om\)nằm giữa hai tia \(Ox;Oz\) (cmt) nên tia \(Oz\)nằm giữa hai tia \(Om;On\) (2)
Từ (1) và (2) suy ra tia \(Oz\) là tia phân giác của \(\widehat {mOn}\).
