Bậc của đa thức \({x^5} - 2{x^2}y - 2x + 9 - {x^5} - y\) là:
-
A
\(5\)
-
B
\(2\)
-
C
\(3\)
-
D
\(9\)
Đáp án của giáo viên lời giải hay : C
Thu gọn đa thức.
Bậc của đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Đa thức \({x^5} - 2{x^2}y - 2x + 9 - {x^5} - y\)\( = \left( {{x^5} - {x^5}} \right) - 2{x^2}y - 2x - y + 9\) \( = - 2{x^2}y - 2x - y + 9\).
Bậc cao nhất của các hạng tử trong đa thức thu gọn trên là \(2 + 1 = 3.\)
Bậc của đa thức đã cho là \(3.\)
Cho tam giác \(ABC\) các đường phân giác \(AM\) của góc \(A\) và \(BN\) của góc \(B\) cắt nhau tại \(I\).
Khi đó, điểm \(I\):
-
A
Là trực tâm của tam giác
-
B
Cách hai đỉnh A và B một khoảng lần lượt bằng \(\dfrac{2}{3}AM\) và \(\dfrac{2}{3}B{\rm N}\)
-
C
Cách đều ba cạnh của tam giác
-
D
Cách đều ba đỉnh của tam giác
Đáp án của giáo viên lời giải hay : C
Tính chất ba đường phân giác trong tam giác: Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ban cạnh của tam giác đó.
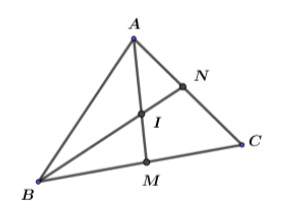
Cho tam giác \(ABC\) các đường phân giác \(AM\) của góc \(A\) và \(BN\) của góc \(B\) cắt nhau tại \(I\)
Khi đó, điểm \(I\) cách đều ba cạnh của tam giác.
Cho hình sau, biết \(G\) là trọng tâm của tam giác \(ABC\). Đẳng thức nào sau đây không đúng?
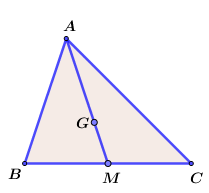
-
A
\(\dfrac{{GM}}{{GA}} = \dfrac{1}{2}\)
-
B
\(\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\)
-
C
\(\dfrac{{AG}}{{GM}} = 2\)
-
D
\(\dfrac{{GM}}{{AM}} = \dfrac{1}{2}\)
Đáp án của giáo viên lời giải hay : D
Tính chất ba đường trung tuyến của một tam giác: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Quan sát hình vẽ và dựa vào tính chất ba đường trung tuyến của một tam giác đã học ta có: \(AG = \dfrac{2}{3}AM\)
\( + )\,\,\dfrac{{GM}}{{GA}} = \dfrac{1}{2}\) nên câu A đúng.
\( + )\,\,\dfrac{{AG}}{{AM}} = \dfrac{2}{3}\) nên câu B đúng.
\( + )\,\,\dfrac{{AG}}{{GM}} = \dfrac{2}{1} = 2\) nên câu C đúng.
\( + )\,\,\dfrac{{GM}}{{AM}} = \dfrac{1}{3}\) nên câu D sai.
Tích của hai đơn thức \(\left( { - 2x{y^3}} \right)\) và \({x^2}y\) là:
-
A
\(2{x^3}{y^4}\)
-
B
\( - 2{x^4}{y^3}\)
-
C
\(2{x^4}{y^4}\)
-
D
\( - 2{x^3}{y^4}\)
Đáp án của giáo viên lời giải hay : D
Để nhân hai đơn thức với nhau ta nhân phần hệ số với nhau và phần biến số với nhau.
Ta có \(\left( { - 2x{y^3}} \right).\left( {{x^2}y} \right) = - 2.\left( {x.{x^2}} \right).\left( {{y^3}.y} \right)\) \( = - 2{x^3}{y^4}.\)
Tam giác \(ABC\) vuông tại A, kẻ \(AH \bot BC\) tại H. Biết \(\widehat {ABC} = {65^0}\). Số
đo \(\widehat {HAC}\) là:
-
A
\({55^0}\)
-
B
\({35^0}\)
-
C
\({25^0}\)
-
D
\({65^0}\)
Đáp án của giáo viên lời giải hay : D
Sử dụng hai góc phụ nhau có số đo bằng \({90^0}.\)
Trong tam giác vuông, hai góc nhọn phụ nhau.
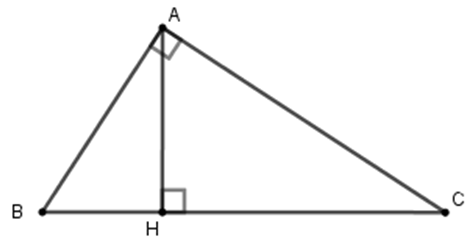
Xét tam giác \(AHB\) vuông tại \(H,\) có \(\widehat {BAH} + \widehat {ABH} = {90^0}\) mà \(\widehat {ABH} = \widehat {ABC} = {65^0}\)
Nên \(\widehat {BAH} = {90^0} - \widehat {ABH} = {90^0} - {65^0}\) \( = {25^0}\)
Lại có \(\widehat {BAH} + \widehat {HAC} = {90^0}\) nên \(\widehat {HAC} = {90^0} - \widehat {BAH} = {90^0} - {25^0}\) \( = {65^0}.\)
Vậy \(\widehat {HAC} = {65^0}.\)
Nếu \(\left| {x - 3,6} \right| = 1,4\) thì giá trị của \(x\) là:
-
A
\(5\)
-
B
\(5\) hoặc \(2,2\)
-
C
\( - 5\)
-
D
\(2,2\)
Đáp án của giáo viên lời giải hay : B
Sử dụng định nghĩa giá trị tuyệt đối \(\left| a \right| = \left\{ \begin{array}{l}a\,\,khi\,\,a \ge 0\\ - a\,\,khi\,\,a < 0\end{array} \right.\)
Ta có \(\left| {x - 3,6} \right| = 1,4\)
TH1: \(x - 3,6 = 1,4\)
\(\begin{array}{l}x = 3,6 + 1,4\\x = 5\end{array}\)
TH2: \(x - 3,6 = - 1,4\)
\(x = 3,6 - 1,4\)
\(x = 2,2\)
Vậy \(x = 5;x = 2,2.\)
Tam giác \(DEF\) vuông tại \(D\) có \(DE = 5cm,{\rm{ }}EF = 13cm\) khi đó số đo cạnh DF bằng:
-
A
\(15cm\)
-
B
\(8cm\)
-
C
\(10cm\)
-
D
\(12cm\)
Đáp án của giáo viên lời giải hay : D
Sử dụng định lý Pytago: “Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”
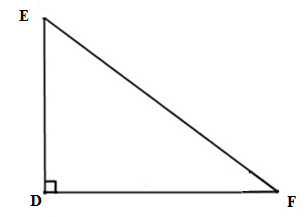
Xét tam giác \(DEF\) vuông tại \(D\), theo định lý Pytago ta có \(D{E^2} + D{F^2} = E{F^2} \Leftrightarrow D{F^2} = E{F^2} - D{E^2}\)
\( \Leftrightarrow D{F^2} = {13^2} - {5^2} = 144 \Rightarrow DF = 12\,cm\)
Vậy \(DF = 12\,cm.\)
Thu gọn đơn thức \(A = {\left( { - 2x{y^3}} \right)^2}.\dfrac{3}{8}x{z^2}\) rồi tìm bậc của đơn thức đó.
-
A
\(A = - \dfrac{3}{2}{x^3}{y^6}{z^2}\) và có bậc \(10\)
-
B
\(A = \dfrac{3}{2}{x^3}{y^6}{z^2}\) và có bậc \(11\)
-
C
\(A = \dfrac{3}{4}{x^2}{y^6}{z^2}\) và có bậc \(6\)
-
D
\(A =- \dfrac{3}{4}{x^3}{y^6}{z^2}\) và có bậc \(11\)
Đáp án của giáo viên lời giải hay : B
Để thu gọn các đơn thức: Thực hiện nhân các đơn thức với nhau.
Muốn nhân hai đơn thức với nhau, ta nhân phần hệ số với nhau và nhân phần biến với nhau, được đơn thức thu gọn.
Bậc của đơn thức thu gọn: Bậc của đơn thức có hệ số khác không là tổng số mũ của tất cả các biến có trong đơn thức đó.
\(\begin{array}{l}A = {\left( { - 2x{y^3}} \right)^2}.\dfrac{3}{8}x{z^2}\\ = \left( { (- 2)^2.\dfrac{3}{8}} \right){\left( {x{y^3}} \right)^2}.x.{z^2}\\ = \dfrac{3}{2}{x^2}.{y^6}.x.{z^2}\\ = \dfrac{3}{2}{x^3}{y^6}{z^2}\end{array}\).
Vậy \(A = \dfrac{3}{2}{x^3}{y^6}{z^2}\).
Bậc của đơn thức: \(3 + 6 + 2 = 11\).
Kết quả của phép tính \(1\dfrac{4}{5} + \dfrac{6}{{29}} - \dfrac{4}{5} + \dfrac{{23}}{{29}}\) là:
-
A
\( - 2\)
-
B
\(4\)
-
C
\(3\)
-
D
\(2\)
Đáp án của giáo viên lời giải hay : D
Sử dụng tính chất giao hoán, kết hợp để tính toán hợp lý.
Ta có:
\(1\dfrac{4}{5} + \dfrac{6}{{29}} - \dfrac{4}{5} + \dfrac{{23}}{{29}} = \left( {1\dfrac{4}{5} - \dfrac{4}{5}} \right) + \left( {\dfrac{6}{{29}} + \dfrac{{23}}{{29}}} \right)\)\( = 1 + 1 = 2\)
Tính hợp lý \(\dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 12}}{{13}}.\dfrac{4}{{17}} + \dfrac{4}{{13}}\) ta được kết quả là:
-
A
\(1\)
-
B
\(\dfrac{{17}}{4}\)
-
C
\(0\)
-
D
\(\dfrac{4}{{17}}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng tính chất phân phối của phép nhân đối với phép cộng: \(A\left( {B + C} \right) = AB + AC\)
Cộng hai phân số cùng mẫu ta cộng tử và giữ nguyên mẫu
Ta có \(\dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 12}}{{13}}.\dfrac{4}{{17}} + \dfrac{4}{{13}}\)
\( = \dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 4}}{{13}}.3.\dfrac{4}{{17}} + \dfrac{4}{{13}}\)
\( = \dfrac{{ - 4}}{{13}}.\dfrac{5}{{17}} + \dfrac{{ - 4}}{{13}}.\dfrac{{12}}{{17}} + \dfrac{4}{{13}}\)
\( = \dfrac{4}{{13}}\left( {\dfrac{{ - 5}}{{17}} + \dfrac{{ - 12}}{{17}} + 1} \right)\)
\( = \dfrac{4}{{17}}.( - 1 + 1) = \dfrac{4}{{17}}.0 = 0\)
Tìm x biết \(x + \dfrac{1}{3} = \dfrac{2}{5} - \left( { - \dfrac{1}{3}} \right)\)
-
A
\(x = \dfrac{2}{5}\)
-
B
\(x = \dfrac{5}{2}\)
-
C
\(x = - \dfrac{2}{5}\)
-
D
\(x = 2\)
Đáp án của giáo viên lời giải hay : A
Tính vế phải trước
Sử dụng: Muốn tìm số hạn chưa biết ta lấy tổng trừ đi số hạng đã biết.
Ta có:
\(x + \dfrac{1}{3} = \dfrac{2}{5} - \left( { - \dfrac{1}{3}} \right) \Leftrightarrow x + \dfrac{1}{3} = \dfrac{2}{5} + \dfrac{1}{3}\)\( \Leftrightarrow x = \dfrac{2}{5}\)
Vậy \(x = \dfrac{2}{5}.\)
Tìm \(x,{\rm{ }}y\) biết \(2x = 3y\) và \(3x + y = 33\)
-
A
\(x = 12; y = 9\)
-
B
\(x = 9;y = 12\)
-
C
\(x = 9;y = 6\)
-
D
\(x = 6;y = 9\)
Đáp án của giáo viên lời giải hay : C
Sử dụng tính chất dãy tỉ số bằng nhau \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{ka + c}}{{kb + d}}\,\,\left( {k \ne 0} \right)\)
Ta có: \(2x = 3y \Rightarrow \dfrac{x}{3} = \dfrac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3} = \dfrac{y}{2} = \dfrac{{3x + y}}{{9 + 2}} = \dfrac{{33}}{{11}} = 3\)
\( \Rightarrow x = 3.3 = 9; y = 2.3 = 6\)
Vậy \(x = 9;y = 6.\)
Cho đa thức \(P\left( x \right) = {x^2} + mx - 9\) (m là tham số). Tìm giá trị của m để \(x = 1\) là một nghiệm của đa thức \(P\left( x \right)\).
-
A
\(m = 8\)
-
B
\(m = 1\)
-
C
\(m = - 8\)
-
D
\(m = - 1\)
Đáp án của giáo viên lời giải hay : A
Ta thay \(x = 1\) vào phương trình \(P\left( x \right) = 0\) để tìm \(m\).
Để \(x = 1\) là nghiệm của \(P\left( x \right) = {x^2} + mx - 9\) ta có:
\(\begin{array}{l}P\left( 1 \right) = 1 + m - 9 = 0\\ \Leftrightarrow m - 8 = 0\\ \Leftrightarrow m = 8\end{array}\).
Vậy \(m = 8\) thì \(x = 1\) là một nghiệm của đa thức \(P\left( x \right)\).
Cho các đa thức \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\); \(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x\).
Sắp xếp các đa thức \(f\left( x \right),\,{\rm{ }}g\left( x \right)\) theo lũy thừa giảm dần của biến.
-
A
\(f\left( x \right) = {x^4} + {x^3} + 3{x^2} + 2x - 4;\) \(g\left( x \right) = {x^4} + {x^3} + 4{x^2} + 3x - 4.\)
-
B
\(f\left( x \right) = {x^4} + {x^3} + 2x - 3{x^2} - 4;\) \(g\left( x \right) = {x^4} + {x^3} + 3x - 4{x^2} - 4.\)
-
C
\(f\left( x \right) = {x^4} + {x^3} - 3{x^2} + 2x - 4;\) \(g\left( x \right) = {x^4} + {x^3} - 4{x^2} + 3x - 4.\)
-
D
\(f\left( x \right) = {x^4} + {x^3} - 3{x^2} + 2x + 4;\) \(g\left( x \right) = {x^4} + {x^3} - 4{x^2} + 3x - 4.\)
Đáp án của giáo viên lời giải hay : C
Thu gọn các đa thức (nếu cần) sau đó sắp xếp theo lũy thừa giảm dần của biến.
Chú ý đến dấu các hạng tử khi sắp xếp.
Ta có: \(f(x) = - 3{x^2} + {x^4} + 2x + {x^3} - 4\)\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)
\(g(x) = {x^3} - 4{x^2} + {x^4} - 4 + 3x \)\(= {x^4} + {x^3} - 4{x^2} + 3x - 4\).
Vậy \(f\left( x \right) = {x^4} + {x^3} - 3{x^2} + 2x - 4;\) \(g\left( x \right) = {x^4} + {x^3} - 4{x^2} + 3x - 4.\)
Tìm đa thức h(x) sao cho \(h(x) = f(x) - g(x)\).
-
A
\(h\left( x \right) = {x^2} + 5x + 8\)
-
B
\(h\left( x \right) = {x^2} + x\)
-
C
\(h\left( x \right) = {x^2} - x\)
-
D
\(h\left( x \right) = {x^2} - x - 8\)
Đáp án của giáo viên lời giải hay : C
Thực hiện phép trừ hai đa thức, nhóm các đơn thức đồng dạng với nhau để thu gọn đa thức thu được.
\(h(x) = f(x) - g(x) = \)(\({x^4} + {x^3} - 3{x^2} + 2x - 4\))\( - ({x^4} + {x^3} - 4{x^2} + 3x - 4)\)
\( = {x^4} + {x^3} - 3{x^2} + 2x - 4\)\( - {x^4} - {x^3} + 4{x^2} - 2x + 4\)
\( = {x^2} - x\).
Vậy \(h\left( x \right) = {x^2} - x\).
Có bao nhiêu nghiệm của đa thức \(h(x)\) với \(h(x)=f(x)-g(x)\).
-
A
\(2\)
-
B
\(3\)
-
C
\(4\)
-
D
\(0\)
Đáp án của giáo viên lời giải hay : A
Sử dụng kết quả câu trước: \(h(x)=f(x)-g(x)= {x^2} - x\)
Nghiệm của đa thức \(P\left( x \right)\) là \(x = a\) nếu \(P\left( a \right) = 0.\)
Theo câu trước ta có: \(h(x)=f(x)-g(x)= {x^2} - x\)
Ta có: \(h(x) = 0 \Leftrightarrow {x^2} - x = 0\).
\( \Leftrightarrow x(x - 1) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Vậy đa thức h(x) các các nghiệm là: \(x = 0;x = 1.\)
Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD\) ( \(D \in AC\)), từ \(D\) kẻ \(DE \bot BC\,(E \in BC)\).
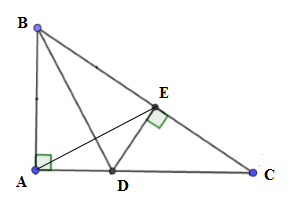
Chọn câu đúng.
-
A
Tam giác \(ABE\) là tam giác cân tại \(B\)
-
B
Tam giác \(ABE\) là tam giác cân tại \(A\)
-
C
Tam giác \(ABE\) là tam giác cân tại \(E\)
-
D
Tam giác \(ADE\) là tam giác cân tại \(A\)
Đáp án của giáo viên lời giải hay : A
Sử dụng cặp tam giác bằng nhau theo trường hợp cạnh huyền góc nhọn.
Xét hai tam giác vuông ABD và EBD có:
BD chung; \(\widehat {ABD} = \widehat {EBD}\) (gt)
\( \Rightarrow \Delta ABD = \Delta EBD \,(ch - gn)\)
\( \Rightarrow BA = BE;DA = DE\) (hai cạnh tương ứng)
Suy ra: \(\Delta ABE\) cân tại \(B\) và \(\Delta ADE\) cân tại D.
So sánh độ dài các đoạn thẳng \(AD\) và \(DC\).
-
A
\(DC > AD\)
-
B
\(DC < AD\)
-
C
\(DC = AD\)
-
D
Không đủ điều kiện so sánh
Đáp án của giáo viên lời giải hay : A
Trong tam giác vuông, cạnh huyền là cạnh có độ dài lớn nhất.
Do tam giác \(DEC\) vuông tại \(C\) nên \(DC > DE;\) mà \(DE = AD\) (theo câu trước)
Suy ra \(DC > AD.\)
Biết \(BE = 12cm;AD = 5cm\). Tính độ dài đoạn thẳng \(BD.\)
-
A
\(12\,cm\)
-
B
\(13\,cm\)
-
C
\(16\,cm\)
-
D
\(15\,cm\)
Đáp án của giáo viên lời giải hay : B
Sử dụng định lý Pytago: “Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”.
Áp dụng định lý Py-ta-go vào tam giác vuông BDE có:
\(B{D^2} = B{E^2} + D{E^2} \Leftrightarrow B{D^2} = BE{}^2 + A{D^2}\) (do \(AD = DE\) (theo câu trước))
\( \Leftrightarrow BD = \sqrt {B{E^2} + A{D^2}} = \sqrt {{{12}^2} + {5^2}} = \sqrt {169} = 13(cm)\).
Cho \(a > 2;b > 2\). Chọn câu đúng.
-
A
\(ab > a + b\)
-
B
\(ab = a + b\)
-
C
\(ab < a + b\)
-
D
\(ab < 4\)
Đáp án của giáo viên lời giải hay : A
Từ điều kiện đề bài lập luận để có: \(\left( {a - 1} \right)\left( {b - 1} \right) > 1\).
Từ đó nhân phá ngoặc để có hệ thức đúng.
Do \(a > 2;\,b > 2 \Rightarrow a - 1 > 1 > 0;b - 1 > 1 > 0\)
\( \Rightarrow (a - 1)(b - 1) > 1 \Leftrightarrow ab - a - b + 1 > 1 \Leftrightarrow ab > a + b\).
Cho đa thức \(f\left( x \right)\) thỏa mãn: \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right)\) với mọi \(x.\) Tìm 5 nghiệm của đa thức \(f\left( x \right)\).
-
A
\(x \in \left\{ {4;2;7;10;13} \right\}\)
-
B
\(x \in \left\{ {4; - 2;7;10;13} \right\}\)
-
C
\(x \in \left\{ {1; - 2;7;10;13} \right\}\)
-
D
\(x \in \left\{ {4; - 2;7;10;11} \right\}\)
Đáp án của giáo viên lời giải hay : B
Thay các giá trị của x làm cho \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right) = 0\).
Tìm được nghiệm ta thay các nghiệm của đa thức \(f\left( x \right)\) vào (1) để tìm tiếp nghiệm. Tìm đủ 5 nghiệm thì dừng lại.
+) Nghiệm của đa thức một biến: Cho đa thức \(P\left( x \right)\). Nếu tại \(x = a\) đa thức \(P\left( x \right)\) có giá trị bằng 0 thì ta nói a là một nghiệm của đa thức \(P\left( x \right)\).
+) Số nghiệm của đa thức một biến.
Một đa thức (khác đa thức không) có thể có \(1;2;3;...;n\) nghiệm hoặc không có nghiệm nào.
Tổng quát: Số nghiệm của một đa thức (khác đa thức 0) không vượt qua bậc của nó.
Ta có: \(f\left( x \right)\) thỏa mãn: \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right)\).
Nếu \(f\left( a \right) = 0 \Rightarrow a\) là một nghiệm của \(f\left( x \right)\).
Vì \(\left( {x - 1} \right).f\left( x \right) = \left( {x + 2} \right)f\left( {x + 3} \right)\) đúng với mọi x.
+) Ta thấy \(x = 1\) thì ta có:
\(\left( {1 - 1} \right)f\left( 1 \right) = \left( {1 + 2} \right)f\left( {1 + 3} \right)\)
\(\Rightarrow 0.f\left( 1 \right) = 3.f\left( 4 \right)\)
\(\Rightarrow 0 = 3.f\left( 4 \right)\)
\( \Rightarrow f\left( 4 \right) = 0\)
\(Hay\,\,\,\,x = 4\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = - 2\) ta được:
\(\left( { - 2 - 1} \right).f\left( { - 2} \right) = \left( { - 2 + 2} \right).f\left( { - 2 + 3} \right)\)
\( \Rightarrow - 3.f\left( { - 2} \right) = 0\)
\( \Rightarrow f\left( { - 2} \right) = 0\)
Hay \( x = - 2\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = 4\) ta được:
\(\left( {4 - 1} \right).f\left( 4 \right) = \left( {4 + 2} \right).f\left( {4 + 3} \right)\)
\( \Rightarrow 3.f\left( 4 \right)\)\( = \,6.f\left( 7 \right)\)
\( \Rightarrow 0= 6f\left( 7 \right)\)\( \Rightarrow f\left( 7 \right) = 0\)
\(Hay\,\,\,\,x = 7\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = 7\) ta tìm được \(f\left( {10} \right) = 0\,\,\,\,hay\,\,\,x = 10\) là một nghiệm của \(f\left( x \right)\)
+) Với \(x = 10\) ta tìm được \(f\left( {13} \right) = 0\,\,\,hay\,\,\,\,x = 13\) là một nghiệm của \(f\left( x \right)\)
Vậy 5 nghiệm của \(f\left( x \right)\) là: \(x \in \left\{ {4; - 2;7;10;13} \right\}\).
