
Một hình thoi có độ dài hai đường chéo là \(m,\,\,n\). Khi đó công thức tính diện tích hình thoi đó là:
A. \(S = (m + n) \times 2\) \(\)
B. \(S = m:n \times 2\)
C. \(S = m \times n\)
D. \(S = \dfrac{{m \times n}}{2}\)
D. \(S = \dfrac{{m \times n}}{2}\)
Diện tích hình thoi bằng tích độ dài hai đường chéo chia cho \(2\) (cùng một đơn vị đo).
Do đó, hình thoi có độ dài hai đường chéo là \(m,\,\,n\) thì diện được tính theo công thức: \(S = \dfrac{{m \times n}}{2}\).

Trong các hình sau, hình nào là hình thoi?
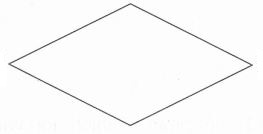
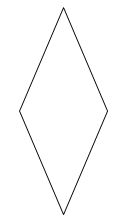
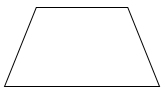



Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Quan sát các hình đã cho ta thấy hình thứ nhất và thứ hai từ trên xuống là hình thoi.
Hình thứ ba là hình thang và hình thứ tư là hình bình hành.

Diện tích hình thoi có độ dài hai đường chéo là \(17cm\) và \(8cm\) là:
A. \(25c{m^2}\)
B. \(50c{m^2}\)
C. \(68c{m^2}\)
D. \(136c{m^2}\)
C. \(68c{m^2}\)
Độ dài hai đường chéo đã có cùng đơn vị đo nên để tính diện tích ta lấy tính tích độ dài hai đường chéo rồi chia cho \(2\).
Diện tích hình thoi đó là:
\(\dfrac{{17 \times 8}}{2} = 68\left( {c{m^2}} \right)\)
Đáp số: \(68c{m^2}\).
Cho hình thoi ABCD, biết \(BD = 18dm\,;\,\,AC = 25dm\).
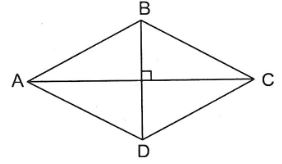
Diện tích hình thoi ABCD là
\(dm^2\).
Diện tích hình thoi ABCD là
\(dm^2\).
Hình thoi đã cho có hai đường chéo là AC và BD. Để tính diện tích ta lấy tích độ dài hai đường chéo chia cho \(2\).
Diện tích hình thoi ABCD là:
\(25 \times 18:2 = 225\left( {d{m^2}} \right)\)
Đáp số: \(225d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(225\).

Điền số thích hợp vào ô trống:
Hình thoi có độ dài các đường chéo là \(37dm\) và \(4m\) có diện tích là:
\(dm^2\).
Hình thoi có độ dài các đường chéo là \(37dm\) và \(4m\) có diện tích là:
\(dm^2\).
Độ dài hai đường chéo chưa cùng đơn vị đo nên ta đổi về cùng đơn vị đo, sau đó để tính diện tích ta lấy tích độ dài hai đường chéo chia cho \(2\).
Đổi: \(4m = 40dm\).
Diện tích hình thoi đó là:
\(37 \times 40:2 = 740\left( {d{m^2}} \right)\)
Đáp số: \(740d{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(740\).

Một hình thoi có diện tích là \(224c{m^2}\) và độ dài đường chéo lớn là \(28cm\) .Vậy độ dài đường chéo bé là:
A. \(8cm\)
B. \(10cm\)
C. \(12cm\)
D. \(16cm\)
D. \(16cm\)
Từ công thức tính diện tích hình thoi: \(S\,= \,\dfrac{{m \times n}}{2}\), ta có thể suy ra công thức tính độ dài một đường chéo là \(m = S \times 2:n\); hoặc \(n = S \times 2:m\).
Độ dài đường chéo bé của hình thoi đó là:
\(224 \times 2:28 = 16\,\,(cm)\)
Đáp số: \(16cm\).
.jpg)
Một mảnh đất dạng hình thoi có độ dài đường chéo bé là \(68m\), độ dài đường chéo lớn gấp đôi đường chéo bé. Diện tích mảnh đất đó là:
A. \(4264{m^2}\)
B. \(4624{m^2}\)
C. \(8528{m^2}\)
D. \(9248{m^2}\)
B. \(4624{m^2}\)
- Tính độ dài đường chéo lớn ta lấy độ dài đường chéo bé nhân với \(2\).
- Tính diện tích mảnh đất đó ta lấy tích độ dài hai đường chéo chia cho \(2\) .
Độ dài đường chéo lớn của mảnh đất đó là:
$68 \times 2 = 136\,\,(m)$
Diện tích của mảnh đất đó là:
$136 \times 68:2 = 4624\,\,({m^2})$
Đáp số: \(4624{m^2}\)
Cho hình vẽ như sau:
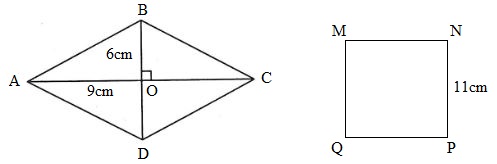
Hình thoi ABCD có O là giao điểm của hai đường chéo, \(OA = 9cm,\,\,OB = 6cm\). Biết rằng hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. Em hãy chọn khẳng định đúng:
A. Diện tích hình thoi bằng diện tích hình vuông.
B. Diện tích hình thoi lớn hơn diện tích hình vuông.
C. Diện tích hình thoi bé hơn diện tích hình vuông.
C. Diện tích hình thoi bé hơn diện tích hình vuông.
- Tính độ dài đường chéo AC, BD: \(AC = OA \times 2\,\,;\,\,\,BD = OB \times 2\,\).
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
- Tính diện tích hình vuông ta lấy cạnh nhân với cạnh.
- So sánh hai số đo diện tích rồi rút ra kết luận.
Độ dài đường chéo AC là:
\(9 \times 2 = 18\,\,(cm)\)
Độ dài đường chéo BD là:
\(6 \times 2 = 12\,\,(cm)\)
Diện tích hình thoi ABCD là:
\(18 \times 12:2 = 108\,(c{m^2})\)
Diện tích hình vuông MNPQ là:
\(11 \times 11 = 121\,(c{m^2})\)
Mà: \(108c{m^2} < 121c{m^2}\)
Vậy diện tích hình thoi bé hơn diện tích hình vuông.
Hình thoi ABCD có độ dài cạnh AB là \(a\).
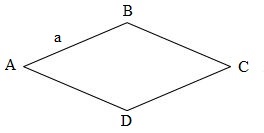
Công thức tính chu vi P của hình thoi là:
\(P = a \times 4\)
Áp dụng công thức trên để tính chu vi hình thoi biết \(a = 38cm\).
A. \(132cm\)
B. \(142cm\)
C. \(152cm\)
D. \(162cm\)
C. \(152cm\)
Thay \(a = 38cm\) vào biểu thức \(P = a \times 4\) rồi tính giá trị biểu thức đó.
Nếu \(a = 36cm\) thì \(P = a \times 4 = 38 \times 4 = 152\,\,(cm)\)
Vậy chu vi hình thoi đó là \(152cm\).
Chọn đáp án đúng hoặc sai cho mỗi khẳng định bên dưới:
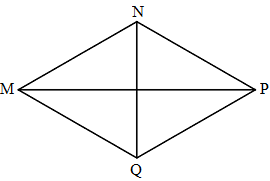
Trong hình thoi MNPQ:
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
MN và PQ không bằng nhau.
MN không song song với MQ
Các cặp cạnh đối diện song song.
MN = NP = PQ = QM
Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.
Trong hình thoi MNPQ ta có:
- Hai cặp cạnh đối diện song song: MN song song với PQ, NP song song với MQ.
- Bốn cạnh bằng nhau: MN = NP = PQ = QM.
Vậy các khẳng định đúng là b,c, d; khẳng định sai là a.
.png)
Điền số thích hợp vào ô trống:
Một thoi có diện tích là \(8d{m^2}\) và độ dài một đường chéo là \(32cm\).
Vậy độ dài đường chéo còn lại là
\(cm\).
Một thoi có diện tích là \(8d{m^2}\) và độ dài một đường chéo là \(32cm\).
Vậy độ dài đường chéo còn lại là
\(cm\).
- Đổi \(8d{m^2}\) sang đơn vị đo là \(c{m^2}\).
- Từ công thức tính diện tích hình thoi: \(S\,\,\, = \,\,\,\dfrac{{m \times n}}{2}\), ta có thể suy ra công thức tính độ dài một đường chéo là: \(m = S \times 2:n\); hoặc \(n = S \times 2:m\).
Đổi: \(8d{m^2} = 800c{m^2}\)
Độ dài đường chéo còn lại là:
\(800 \times 2:32 = 50\,\,(cm)\)
Đáp số: \(50cm\).
Vậy đáp án đúng điền vào ô trống là \(50\).
Điền số thích hợp vào ô trống:
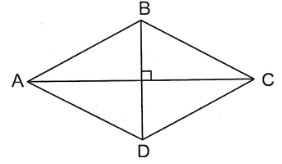
Cho hình thoi ABCD. Biết $AC = 36cm$, độ dài đường chéo BD bằng \(\dfrac{3}{4}\) độ dài đường chéo AC.
Vậy diện tích hình thoi đó là
\(cm^2\).

Cho hình thoi ABCD. Biết $AC = 36cm$, độ dài đường chéo BD bằng \(\dfrac{3}{4}\) độ dài đường chéo AC.
Vậy diện tích hình thoi đó là
\(cm^2\).
- Tính độ dài đường chéo BD ta lấy độ dài đường chéo AC nhân với \(\dfrac{3}{4}\).
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).
Độ dài đường chéo BD là:
\(36 \times \dfrac{3}{4} = 27\;(cm)\)
Diện tích của hình thoi ABCD là:
$36 \times 27:2 = 486\;(c{m^2})$
Đáp số: \(486c{m^2}\).
Vậy đáp án đúng điền vào ô trống là \(486\).
Cho hình vẽ như sau:
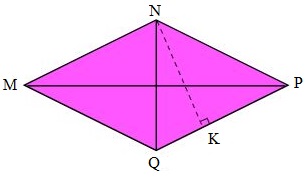
Hình thoi MNPQ có độ dài cạnh là \(32cm\). Tổng độ dài hai đường chéo là \(84cm\), hiệu độ dài hai đường chéo là \(12cm\). Độ dài chiều cao NK là:
A. \(27cm\)
B. \(36cm\)
C. \(54cm\)
D. \(72cm\)
A. \(27cm\)
- Ta có tổng và hiệu của hai đường chéo. Ta sẽ tìm hai đường chéo theo công thức tìm hai số khi biết tổng và hiệu của hai số đó:
Số lớn = (Tổng + Hiệu) \(:\,\,2\) ; Số bé = (Tổng – hiệu) \(:\,\,2\)
- Tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\) .
- Vì hình thoi có các cặp cạnh đối diện song song và bằng nhau nên hình thoi cũng chính là hình bình hành. Để tính độ dài chiều cao NK ta lấy diện tích chia cho độ dài cạnh đáy PQ.
Ta có sơ đồ:
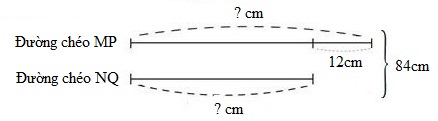
Độ dài đường chéo MP là:
\((84 + 12):2 = 48\left( {cm} \right)\)
Độ dài đường chéo NQ là:
\(84 - 48 = 36\,\,\left( {cm} \right)\)
Diện tích hình thoi đó là:
\(48 \times 36:2 = 864\left( {{m^2}} \right)\)
Độ dài chiều cao NK là:
\(864:32 = 27\,\,(cm)\)
Đáp số: \(27cm\).

Điền số thích hợp vào ô trống:
Một hình thoi có diện tích bằng diện tích của hình chữ nhật có chiều dài \(75cm\), chiều rộng kém chiều dài $33cm$. Biết đường chéo thứ nhất của hình thoi dài \(50cm\).
Vậy độ dài đường chéo còn lại của hình thoi là
\(cm\).
Một hình thoi có diện tích bằng diện tích của hình chữ nhật có chiều dài \(75cm\), chiều rộng kém chiều dài $33cm$. Biết đường chéo thứ nhất của hình thoi dài \(50cm\).
Vậy độ dài đường chéo còn lại của hình thoi là
\(cm\).
- Tính số đo chiều rộng ta lấy số đo chiều dài trừ đi $33cm$.
- Tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng.
Từ đó ta có diện tích hình thoi.
- Tính độ dài đường chéo còn lại ta lấy \(2\) lần diện tích hình thoi chia cho độ dài đường chéo đã biết.
Chiều rộng của hình chữ nhật là:
\(75 - 33 = 42\,(cm)\)
Diện tích hình chữ nhật là:
\(75 \times 42 = 3150\,(c{m^2})\)
Vậy diện tích hình thoi là \(3150c{m^2}\).
Độ dài đường chéo còn lại của hình thoi là:
$3150 \times 2:50 = 126{\rm{ }}\left( {cm} \right)$
Đáp số: \(126cm\).
Vậy đáp án đúng điền vào ô trống là \(126\).
