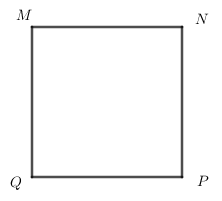
Cho hình vuông \(MNPQ\), khẳng định nào sau đây đúng?
-
A
\(MN\) và \(PQ\) song song
-
B
\(MN\) và \(NP\) song song
-
C
\(MQ\) và \(PQ\) song song
-
D
\(MN\) và \(MQ\) song song
Đáp án của giáo viên lời giải hay : A
Trong hình vuông, hai cặp cạnh đối song song với nhau.
Trong hình vuông \(MNPQ\) có hai cặp cạnh đối song song với nhau là:
+ \(MN\) và \(PQ\).
+ \(MQ\) và \(NP\)
=> Đáp án A đúng.
Chọn phát biểu sai?
-
A
Hình vuông có bốn cạnh bằng nhau
-
B
Hình vuông có bốn cặp cạnh đối song song
-
C
Hình vuông có hai đường chéo bằng nhau
-
D
Hình vuông có bốn góc bằng nhau
Đáp án của giáo viên lời giải hay : B
Sử dụng dấu hiệu nhận biết của hình vuông.
Hình vuông có hai cặp cạnh đối song song => Đáp án B sai.
Phát biểu nào sau đây sai?
-
A
Hình lục giác đều có 6 đỉnh
-
B
Hình lục giác đều có 6 cạnh
-
C
Hình lục giác đều có 6 đường chéo chính
-
D
Hình lục giác đều có 6 góc
Đáp án của giáo viên lời giải hay : C
Sử dụng dấu hiệu nhận biết lục giác đều.
Các đáp án A, B, D đúng.
Hình lục giác đều có 3 đường chéo chính => Đáp án C sai.
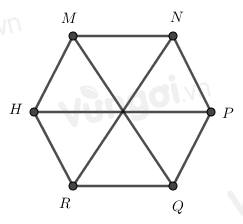
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
-
A
\(MQ = NR\)
-
B
\(MH = RQ\)
-
C
\(MN = HR\)
-
D
\(MH = MQ\)
Đáp án của giáo viên lời giải hay : D
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Hình lục giác đều MNPQRH có 3 đường chéo chính bằng nhau nên: \(MQ = NR\)
=> A đúng
Hình lục giác đều MNPQRH có 6 cạnh bằng nhau nên \(MH = RQ\) và \(MN = HR\)
=> B, C đúng.
Do MH là cạnh, MQ là đường chéo chính nên hai đoạn này không bằng nhau
=> D sai
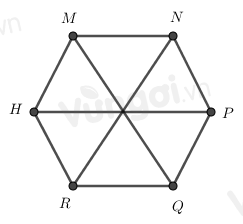
Cho hình lục giác đều MNPQRH, có bao nhiêu tam giác đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
-
A
8
-
B
2
-
C
4
-
D
6
Đáp án của giáo viên lời giải hay : D
Đếm số tam giác đều đều được tạo thành từ các đường chéo chính có cạnh bằng cạnh của lục giác đều
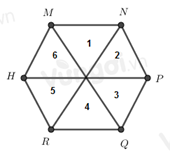
Ta đánh số như hình trên
Nhận thấy có các hình tam giác đều là: 1, 2, 3, 4, 5, 6.
Vậy có 6 tam giác đều.
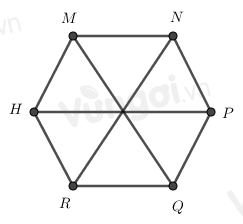
Cho hình lục giác đều MNPQRH, phát biểu nào sai?
-
A
6 đỉnh là M, N, P, Q, R, H
-
B
6 cạnh là MN, NP, PQ, MQ, QR, HM
-
C
3 đường chéo chính là MQ, HP, RN.
-
D
3 đường chéo chính cắt nhau tại 1 điểm.
Đáp án của giáo viên lời giải hay : B
- Trong hình lục giác đều:
+ 6 cạnh bằng nhau
+ 3 đường chéo chính bằng nhau.
Đáp án B sai do MQ là đường chéo chính, sửa lại:
6 cạnh là MN, NP, PQ, HR, QR, HM
Chọn phát biểu sai:
-
A
Tam giác đều có ba cạnh
-
B
Ba cạnh của tam giác đều bằng nhau
-
C
Bốn góc của tam giác đều bằng nhau
-
D
Tam giác đều có ba đỉnh
Đáp án của giáo viên lời giải hay : C
Trong tam giác đều ba góc bằng nhau => Đáp án C sai.
Cho tam giác đều \(MNP\) có \(MN = 5\,cm\), khẳng định nào sau đây đúng?
-
A
\(NP = 3\,cm\)
-
B
\(MP = 4\,cm\)
-
C
\(NP = 6\,cm\)
-
D
\(MP = 5\,cm\)
Đáp án của giáo viên lời giải hay : D
Trong tam giác đều ba cạnh bằng nhau mà \(MN = 5\,cm\) nên ta có: \(MN = NP = MP = 5\,cm\)
=> Chọn D
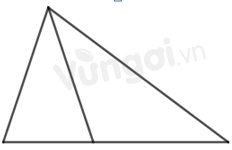
Hình dưới đây có mấy hình tam giác?
-
A
1
-
B
2
-
C
3
-
D
4
Đáp án của giáo viên lời giải hay : C
Đếm số hình tam giác nhỏ + số hình tam giác tạo từ các hình tam giác nhỏ
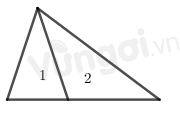
Hình trên có 2 hình tam giác nhỏ là: 1, 2 và 1 hình tam giác lớn ghép từ hai hình trên
=> Có tất cả 3 hình tam giác
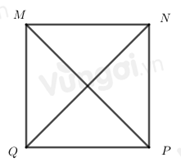
Cho hình vuông \(MNPQ\), khẳng định nào sau đây sai?
-
A
\(MN = PQ\)
-
B
\(MQ = QP\)
-
C
\(MN = NP\)
-
D
\(MN = MP\)
Đáp án của giáo viên lời giải hay : D
Trong hình vuông:
- Bốn cạnh bằng nhau.
- Hai đường chéo bằng nhau.
Hình vuông \(MNPQ\) có: \(MN = NP = PQ = MQ\)
=> Đáp án A, B, C đúng.
Đáp án D sai do \(MN\) là cạnh của hình vuông, \(MP\) là đường chéo nên \(MN = MP\) là sai.
Hình dưới đây có tất cả bao nhiêu hình vuông?

-
A
9
-
B
14
-
C
10
-
D
13
Đáp án của giáo viên lời giải hay : B
Đếm số hình vuông nhỏ + số hình vuông được ghép từ các ô vuông nhỏ.
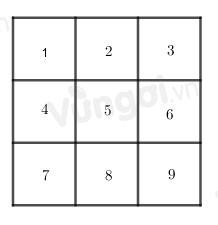
Ta đánh số như hình trên:
+ 9 hình vuông nhỏ là: 1, 2, 3, 4, 5, 6, 7, 8, 9.
+ 4 hình vuông được gép từ bốn hình vuông nhỏ là: 1245, 2356, 4578, 5689.
+ 1 hình vuông lớn được ghép từ 9 hình vuông nhỏ.
Vậy có tất cả \(9 + 4 + 1 = 14\) hình vuông.
