
Héc-tô-mét vuông còn gọi là héc-ta hay ha. Đúng hay sai ?
A. Đúng
B. Sai
A. Đúng
Dựa vào cách viết khác của đơn vị héc-tô-mét vuông.
Héc-tô-mét vuông còn gọi là héc-ta hay ha.

Cho các phân số sau: \(\dfrac{3}{5};\dfrac{2}{3};\dfrac{7}{{10}};\dfrac{{27}}{{50}}\).
Trong các phân số trên, phân số nào là phân số thập phân?
A. \(\dfrac{3}{5}\)
B.\(\dfrac{2}{3}\)
C. \(\dfrac{7}{{10}}\)
D. \(\dfrac{{27}}{{50}}\)
C. \(\dfrac{7}{{10}}\)
Các phân số có mẫu số là $10;{\rm{ }}100;{\rm{ }}1000...$ được gọi là phân số thập phân.
Các phân số có mẫu số là $10;{\rm{ }}100;{\rm{ }}1000...$ được gọi là phân số thập phân.
Mà trong các phân số trên ta thấy số phân số \(\dfrac{7}{{10}}\) có mẫu số là \(10.\) Vậy phân số \(\dfrac{7}{{10}}\) là phân số thập phân.

Chọn dấu thích hợp để điền vào chỗ trống :
\(\dfrac{5}{7}\) $...$ \(1\)
A. \( = \)
B. \( > \)
C. \( < \)
C. \( < \)
Phân số nào có tử số nhỏ hơn mẫu số thì phân số đó nhỏ hơn \(1.\)
Phân số nào có tử số lớn hơn mẫu số thì phân số đó lớn hơn \(1\).
Phân số nào có tử số bằng mẫu số thì phân số đó lớn hơn \(1\).
Phân số \(\dfrac{5}{7}\) có \(5 < 7\) nên \(\dfrac{5}{7} < 1.\)

$23{\rm{ }}dm{\rm{ }} = $ \(...cm\).
Số thích hợp điền vào chỗ trống là:
A. \(230\)
B. \(2300\)
C. \(23000\)
D. \(230000\)
A. \(230\)
Áp dụng nhận xét: Trong bảng đơn vị đo độ dài, hai đơn vị liền nhau hơn (kém) nhau \(10\) lần.
Ta thấy \(dm\) và \(cm\) là hai đơn vị đo độ dài liền nhau.
Ta có \(1dm = 10cm\) nên \(23dm = 230cm\)
(vì \(10 \times 23 = 230\))
Vậy số thích hợp điền vào chỗ trống là \(230\).

Điền số thích hợp vào ô trống:
\(25\) tấn \( = \)
tạ.
\(25\) tấn \( = \)
tạ.
Áp dụng nhận xét, trong bảng đơn vị đo khối lượng, hai đơn vị đo liền nhau hơn (kém) nhau $10$ lần.
Ta thấy hai đơn vị tấn và tạ là hai đơn vị đo khối lượng liền nhau.
Ta có \(1\) tấn = \(10\) tạ nên \(25\) tấn = \(250\) tạ (vì \(10 \times 25 = 250\))
Vậy số thích hợp điền vào chỗ trống là \(250\).

Rút gọn phân số sau thành phân số tối giản:
- Khi rút gọn phân số ta xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào lớn hơn $1,$ sau đó chia cả tử số và mẫu số cho số tự nhiên đó, cứ làm như thế cho đến khi nhận được phân số tối giản.
- Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\).
Ta thấy phân số \(\dfrac{{16}}{{52}}\) có tử số là \(16\), mẫu số là \(52\). Mà \(16\) và \(52\) đều chia hết cho \(4\).
Do đó ta có: \(\dfrac{{16}}{{52}} = \dfrac{{16:4}}{{52:4}} = \dfrac{4}{{13}}\)
Phân số \(\dfrac{4}{{13}}\) là phân số tối giản (vì \(4\) và \(13\) không cùng chia hết cho số tự nhiên nào lớn hơn \(1\)).
Vậy rút gọn phân số \(\dfrac{{16}}{{52}}\) ta được phân số tối giản là \(\dfrac{4}{{13}}\).
Số thích hợp điền vào ô trống theo thứ tự từ trên xuống dưới là \(4;\,13\).

Tính rồi rút gọn (nếu được) : \(\dfrac{7}{5} - \dfrac{5}{6} + \dfrac{1}{3}\)
A. \(\dfrac{7}{{30}}\)
B. \(\dfrac{{27}}{{30}}\)
C. \(\dfrac{{17}}{{10}}\)
D. \(\dfrac{9}{{10}}\)
D. \(\dfrac{9}{{10}}\)
- Phép tính chỉ có phép tính cộng và trừ nên ta tính lần lượt từ trái sang phải.
- Để cộng hoặc trừ hai phân số, ta quy đồng mẫu số hai phân số rồi cộng hoặc trừ hai phân số đã quy đồng.
$\dfrac{7}{5} - \dfrac{5}{6} + \dfrac{1}{3} $$= \dfrac{{42}}{{30}} - \dfrac{{25}}{{30}} + \dfrac{1}{3} $$= \dfrac{{17}}{{30}} + \dfrac{1}{3} $$= \dfrac{{17}}{{30}} + \dfrac{{10}}{{30}} $$= \dfrac{{27}}{{30}} $$= \dfrac{9}{{10}}$

Thực hiện phép tính $2\dfrac{2}{3}:4\dfrac{1}{5}$ ta được kết quả là phân số tối giản có tử số là
Thực hiện phép tính $2\dfrac{2}{3}:4\dfrac{1}{5}$ ta được kết quả là phân số tối giản có tử số là
- Có thể viết hỗn số thành một phân số như sau:
+ Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số
+ Mẫu số bằng mẫu số ở phần phân số
- Sau khi đổi sang phân số ta thực hiện chia hai phân số.
$2\dfrac{2}{3}:4\dfrac{1}{5} $$= \dfrac{8}{3}:\dfrac{{21}}{5} $$= \dfrac{8}{3} \times \dfrac{5}{{21}} $$= \dfrac{{40}}{{63}}$
Ta có $\dfrac{{40}}{{63}}$ là phân số tối giản có tử số là \( 40\).
Vậy số thích hợp điền vào ô trống là $40$.

Chọn dấu thích hợp để điền vào chỗ trống:
$5m\;{\rm{ 2}}cm$ $...$ $52{\rm{0}}cm$
A. \( > \)
B. \( < \)
C. \( = \)
B. \( < \)
- Đổi về cùng một đơn vị đo là \(cm\) rồi so sánh.
- Áp dụng cách đổi \(1m=100cm\) để đổi \(5m\) sang đơn vị đo là \(cm\).
Ta có: $1m{\rm{ }} = {\rm{ }}100cm$ nên $5m{\rm{ }} = {\rm{ 5}}00cm.$
$5m\;{\rm{ 2}}cm = {\rm{5}}m + 2cm = {\rm{5}}00cm + {\rm{2}}cm = {\rm{502}}cm.$
Mà $502cm < 520cm$.
Vậy $5m\;2cm\; < \;520cm$.

Có \(14\) người làm xong một công việc trong \(5\) ngày. Hỏi nếu có \(35\) người thì sẽ làm xong công việc đó trong bao nhiêu ngày? (biết mức làm của mỗi người là như nhau).
A. \(2\) ngày
B. \(4\) ngày
C. \(6\) ngày
D. \(8\) ngày
A. \(2\) ngày
+ Để làm xong một công việc, càng có nhiều người thì thời gian hoàn thành công việc đó càng giảm. Vậy đây là bài toán tỉ lệ nghịch.
+ Với dạng bài về quan hệ tỉ lệ, ta có thể làm theo 2 cách sau:
Cách 1: Dùng phương pháp rút về đơn vị.
Cách 2: Dùng phương pháp tìm tỉ số: số người tăng lên bao nhiêu lần thì số ngày làm phải giảm đi bấy nhiêu lần.
Tóm tắt:
\(14\) người : \(5\) ngày
\(35\) người : … ngày?
(Phương pháp rút về đơn vị)
Một người làm xong công việc đó trong số ngày là:
\(14 \times 5 = 70\) (ngày)
Nếu có \(35\) người thì sẽ làm xong công việc đó trong số ngày là:
$70:35 = 2$ (ngày)
Đáp số: \(2\) ngày.

Chọn dấu thích hợp để điền vào chỗ trống:
\(2h{m^2}\;5da{m^2}\) $...$ \(2005da{m^2}\)
A. \( > \)
B. \( = \)
C. \( < \)
C. \( < \)
Đổi về cùng một đơn vị đo là \(dam^2\) rồi so sánh.
Ta có:
\(2h{m^2} = 200da{m^2}\)
\(2h{m^2}5da{m^2} \)\(= 2h{m^2} + 5da{m^2} \)\(= 200h{m^2} + 5da{m^2} \)\(= 205da{m^2}\)
Vì \(205da{m^2} < 2005da{m^2}\) nên \(2h{m^2}5da{m^2} < 2005da{m^2}\).
 \(\dfrac{3}{5}\) của \(15h{m^2}\) bằng bao nhiêu \({m^2}\)?
\(\dfrac{3}{5}\) của \(15h{m^2}\) bằng bao nhiêu \({m^2}\)?
A. $9$
B. $900$
C. $9000$
D. $90000$
D. $90000$
Đây là dạng bài tìm một phân số của một số, muốn tìm một phân số của một số ta lấy số đó nhân với phân số đã cho.
Ta sẽ tìm \(\dfrac{3}{5}\) của \(15h{m^2}\) là bao nhiêu \(h{m^2}\), sau đó đổi ra đơn vị \({m^2}\); lưu ý rằng \(1hm^2=10000m^2\).
\(\dfrac{3}{5}\) của \(15h{m^2}\) là: \(15 \times \dfrac{3}{5} = 9\left( {h{m^2}} \right)\)
Đổi \(9h{m^2} = 90000{m^2}\).
Vậy: \(\dfrac{3}{5}\) của \(15h{m^2}\) là \(90000{m^2}\).

Hiện nay tuổi An bằng \(\dfrac{3}{5}\) tuổi Bình. Ba năm trước An kém Bình \(8\) tuổi. Tính số tuổi mỗi người hiện nay.
A. An \(5\) tuổi, Bình \(13\) tuổi
B. An \(12\) tuổi, Bình \(20\) tuổi
C. An \(6\) tuổi, Bình \(14\) tuổi
D. An \(9\) tuổi, Bình \(15\) tuổi
B. An \(12\) tuổi, Bình \(20\) tuổi
- Vì hiệu số tuổi của hai bạn không thay đổi theo thời gian nên hiện nay An vẫn kém Bình \(8\) tuổi.
- Hiện nay tuổi An bằng \(\dfrac{3}{5}\) tuổi Bình hay tỉ số về số tuổi của An và Bình là \(\dfrac{3}{5}\). Ta biểu diễn số tuổi của An hiện nay là \(3\) phần bằng nhau, số tuổi của Bình hiện nay là \(5\) phần như thế. Coi tuổi An là số bé, tuổi Bình là số lớn, ta tìm hai số theo công thức:
Số bé = Giá trị một phần × số phần của số bé
hoặc
Số lớn = Giá trị một phần × số phần của số lớn.
Vì hiệu số tuổi của hai bạn không thay đổi theo thời gian, ba năm trước An kém Bình \(8\) tuổi nên hiện nay An vẫn kém Bình \(8\) tuổi.
Ta có sơ đồ số tuổi hai bạn hiện nay:
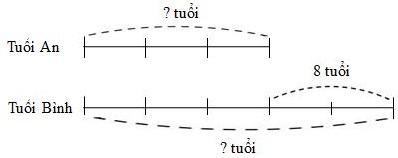
Theo sơ đồ, hiệu số phần bằng nhau là:
\(5 - 3 = 2\) (phần)
Giá trị một phần là:
\(8:2 = 4\) (tuổi)
Tuổi An hiện nay là:
\(4 \times 3 = 12\) (tuổi)
Tuổi Bình hiện nay là:
\(12 + 8 = 20\) (tuổi)
Đáp số: An \(12\) tuổi; Bình \(20\) tuổi.

Điền số thích hợp vào ô trống:
Hai bao có tất cả $120kg$ gạo. Nếu chuyển $20kg$ gạo từ bao thứ nhất sang bao thứ hai thì bao thứ hai nhiều hơn bao thứ nhất $12kg$ gạo.
Vậy lúc đầu bao thứ nhất có
\(kg\) gạo, bao thứ hai có
\(kg\) gạo.
Hai bao có tất cả $120kg$ gạo. Nếu chuyển $20kg$ gạo từ bao thứ nhất sang bao thứ hai thì bao thứ hai nhiều hơn bao thứ nhất $12kg$ gạo.
Vậy lúc đầu bao thứ nhất có
\(kg\) gạo, bao thứ hai có
\(kg\) gạo.
- Chuyển $20kg$ gạo từ bao thứ nhất sang bao thứ hai thì tổng số gạo ở hai bao không thay đối.
- Khi đó ta có bài toán tìm hai số khi biết tổng và hiệu, coi số gạo lúc sau của bao thứ nhất là số bé, số gạo lúc sau của bao thứ hai là số lớn, ta tìm hai số theo công thức:
Số bé = (tổng – hiệu) : \(2\)
Số lớn = (tổng + hiệu) : \(2\)
- Tìm số gạo lúc đầu của bao thứ nhất là lấy số gạo lúc sau của bao thứ nhất cộng với \(20kg\).
- Tìm số gạo lúc đầu của bao thứ hai ta lấy tổng số gạo của hai bao trừ đi số gạo lúc đầu của bao thứ nhất.
Chuyển $20kg$ gạo từ bao thứ nhất sang bao thứ hai thì tổng số gạo ở hai bao không thay đối.
Ta có sơ đồ biểu diễn số gạo lúc sau của hai bao:
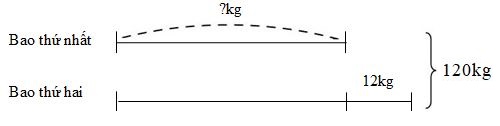
Lúc sau bao thứ nhất có số ki-lô-gam gạo là:
\((120 - 12):2 = 54\;(kg)\)
Lúc đầu bao thứ nhất có số ki-lô-gam gạo là:
\(54 + 20 = 74\;(kg)\)
Lúc đầu bao thứ hai có số ki-lô-gam gạo là:
\(120 - 74 = 46\;(kg)\)
Đáp số: Bao thứ nhất \(74kg\);
Bao thứ hai \(46kg\).
Vậy số thích hợp điền vào ô trống theo thứ tự từ trên xuống dưới là \(74;\,46\).

Một người nuôi \(112\) con gà. Sau khi người đó mua thêm \(38\) con gà mái và bán đi \(15\) con gà trống thì lúc này số gà trống bằng \(\dfrac{4}{5}\) số gà mái. Hỏi lúc đầu người đó nuôi bao nhiêu con gà trống, bao nhiêu con gà mái?
A. \(40\) con gà trống, \(72\) con gà mái
B. \(75\) con gà trống, \(37\) con gà mái
C. \(75\) con gà trống, \(60\) con gà mái
D. \(45\) con gà trống, \(67\) con gà mái
B. \(75\) con gà trống, \(37\) con gà mái
- Đề bài cho tổng số gà ban đầu nhưng lại cho tỉ số giữa gà trống và gà mái lúc sau, tức là sau khi mua thêm \(38\) con gà mái và bán đi \(15\) con gà trống . Để tính được lúc đầu người đó có bao nhiêu con gà mỗi loại, ta sẽ đi tìm số gà mỗi loại lúc sau.
- Sau khi người đó mua thêm \(38\) con gà mái và bán đi \(15\) con gà trống thì tổng số con gà là:
$112 + 38 - 15 = 135$ (con)
Theo đề bài, lúc sau số gà trống bằng \(\dfrac{4}{5}\) số gà mái nên ta biểu diễn số gà trống lúc sau bằng \(4\) phần bằng nhau, số gà mái lúc sau bằng \(5\) phần như thế. Coi số gà trống là số bé, số gà mái là số lớn, ta tìm hai số theo công thức:
Số bé = Giá trị một phần × số phần của số bé
hoặc
Số lớn = Giá trị một phần × số phần của số lớn.
- Tìm số gà mái ban đầu ta lấy số gà mái lúc sau trừ đi \(38.\)
- Tìm số gà trống ban đầu ta lấy tổng số gà ban đầu trừ đi số gà mái ban đầu.
Sau khi người đó mua thêm \(38\) con gà mái và bán đi \(15\) con gà trống thì tổng số con gà là:
$112 + 38 - 15 = 135$ (con)
Ta có sơ đồ biểu diễn số gà lúc sau:
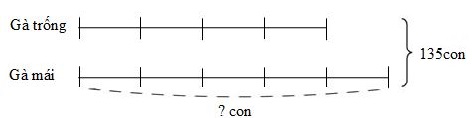
Theo sơ đồ, tổng số phần bằng nhau là:
$4 + 5 = 9$ (phần)
Giá trị một phần là:
\(135:9 = 15\) (con)
Số gà mái lúc sau là:
\(15 \times 7 = 75\) (con)
Lúc đầu người đó nuôi số con gà mái là:
\(75 - 38 = 37\) (con)
Lúc đầu người đó nuôi số con gà trống là:
\(112 - 37 = 75\) (con)
Đáp số: \(75\) con gà trống;
\(37\) con gà mái.
