Hai tụ điện \({C_1} = {\rm{ }}{C_2}\) mắc song song. Nối hai đầu bộ tụ với ắc qui có suất điện động \(E{\rm{ }} = {\rm{ }}6V\) để nạp điện cho các tụ rồi ngắt ra và nối với cuộn dây thuần cảm \(L\) để tạo thành mạch dao động. Sau khi dao động trong mạch đã ổn định, tại thời điểm dòng điện qua cuộn dây có độ lớn bằng một nữa giá trị dòng điện cực đại, người ta ngắt khóa K để cho mạch nhánh chứa tụ \({C_2}\) hở. Kể từ đó, hiệu điện thế cực đại trên tụ còn lại \({C_1}\) là:
-
A
\(3\sqrt 3 V\)
-
B
\(3V\)
-
C
\(3\sqrt 5 V\)
-
D
\(\sqrt 2 V\)
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức tính năng lượng : \({\rm{W}} = \frac{1}{2}CU_0^2\)
+ Năng lượng từ trường: \({{\rm{W}}_L} = \frac{1}{2}L{i^2}\)
Gọi \({C_0}\) là điện dung của mỗi tụ điên.
Năng lượng của mạch dao động khi chư ngắt tụ \({C_2}\)
\({W_0} = \frac{{C{U^2}}}{2} = \frac{{2{C_0}{E^2}}}{2} = 36{C_0}\)
Khi \(i = \frac{{{I_0}}}{2}\), năng lượng từ trường \({W_L} = {\rm{ }}L{i^2} = \frac{1}{4}\frac{{LI_0^2}}{2} = \frac{{{W_0}}}{4} = 9{C_0}\)
Khi đó năng lượng điên trường: \({W_C} = \frac{{3{W_0}}}{4} = 27{C_0}\)
Năng ượng điên trường của mỗi tụ: \({W_{{C_1}}} = {W_{{C_2}}} = {\rm{ }}13,5{C_0}\)
Sau khi ngắt một tụ năng lượng còn lại của mạch là: \(W = {W_L} + {W_{{C_1}}} = 22,5{C_0}\)
\(W = \frac{{{C_1}U_1^2}}{2} = \frac{{{C_0}U_1^2}}{2} = 22,5{C_0}\)
\( \to U_1^2 = 45 \to {U_1} = 3\sqrt 5 V\)
Hai tụ điện \({C_1} = {\rm{ }}3{C_0}\) và \({C_2} = {\rm{ }}6{C_0}\) mắc nối tiếp. Nối hai đầu bộ tụ với pin có suất điện động \(E{\rm{ }} = {\rm{ }}3V\) để nạp điện cho các tụ rồi ngắt ra và nối với cuộn dây thuần cảm \(L\) tạo thành mạch dao động điện từ tự do. Tại thời điểm dòng điện qua cuộn dây có độ lớn bằng một nửa giá trị dòng điện đạt cực đại, thì người ta nối tắt hai cực của tụ \({C_1}\). Điện áp cực đại trên tụ \({C_2}\) của mạch dao động sau đó:
-
A
\(\dfrac{{\sqrt 6 }}{2}V\)
-
B
\(\dfrac{{3\sqrt 3 }}{2}V\)
-
C
\(\sqrt 6 V\)
-
D
\(\sqrt 3 V\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức tính điện dung của bộ tụ khi mắc nối tiếp: \(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + ... + \frac{1}{{{C_n}}}\)
+ Sử dụng biểu thức mối liên hệ giữa điện tích – điện dung – suất điện động: \(Q = CE\)
+ Sử dụng biểu thức tính năng lượng từ trường: \({{\rm{W}}_L} = \frac{1}{2}L{i^2}\)
+ Ta có hai tụ mắc nối tiếp,
=> Điện dung của bộ tụ:
\(\begin{array}{l}\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} = \frac{1}{{3{C_0}}} + \frac{1}{{6{C_0}}} = \frac{1}{{2{C_0}}}\\ \to C = {\rm{ }}2{C_0}\end{array}\)
+ Điện tích của bộ tụ \({Q_0} = {\rm{ }}EC{\rm{ }} = {\rm{ }}6{C_0}\)
Năng lượng ban đầu của mạh \({W_0} = \frac{{Q_0^2}}{{2C}} = \frac{{{{\left( {6{C_0}} \right)}^2}}}{{2.2{C_0}}} = 9{C_0}\)
+ Khi \(i = \frac{{{I_0}}}{2}\): \({W_L} = \frac{{L{i^2}}}{2} = \frac{{LI_0^2}}{8} = \frac{{{{\rm{W}}_0}}}{4} = \frac{{9{C_0}}}{4} = 2,25{C_0}\)
Năng lượng của hai tụ khi đó \({W_{C1}} + {\rm{ }}{W_{C2}} = \frac{{3{W_0}}}{4} = \frac{{3.9{C_0}}}{4} = 6,75{C_0}\) (1)
Mặt khác khi hai tụ mắc nối tiếp \(\frac{{{W_{{C_1}}}}}{{{W_{{C_2}}}}} = \frac{{{C_2}}}{{{C_1}}} = 2\) (2)
Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}{{\rm{W}}_{{C_1}}} = 4,5{C_0}\\{W_{{C_2}}} = 2,25{C_0}\end{array} \right.\)
+ Sau khi nối tắt tụ \({C_1}\) năng lượng của mạch \(L{C_2}\): \(W{\rm{ }} = {\rm{ }}{W_L} + {\rm{ }}{W_{C2}} = 2,25{C_0}{\rm{ + 2}}{\rm{,25}}{{\rm{C}}_0}{\rm{ = }}4,5{C_0}\)
Lại có:
\(\begin{array}{l}{\rm{W}} = \frac{1}{2}{C_2}U_{02}^2 = 4,5{C_0} \leftrightarrow \frac{1}{2}6{C_0}U_{02}^2 = 4,5{C_0}\\ \to {U_{02}} = \sqrt {\frac{3}{2}} = \frac{{\sqrt 6 }}{2}V\end{array}\)
Hai tụ \({C_1} = 3{C_0}\) và \({C_2} = {\rm{ }}6{C_0}\) mắc nối tiếp. Nối \(2\) đầu bộ tụ với pin có suất điện động \(E = {\rm{ }}3V\) để nạp điện cho các tụ rồi ngắt ra và nối với cuộn dây thuần cảm L tạo thành mạch dao động điện từ tự do. Khi dòng điện trong mạch dao động đạt cực đại thì người ta nối tắt 2 cực của tụ \({C_1}\). Hiệu điện thế cực đại trên tụ \({C_2}\) của mạch dao động sau đó là:
-
A
1 V
-
B
\(\sqrt 3 V\)
-
C
2 V
-
D
3 V
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính điện dung của bộ tụ khi mắc nối tiếp: \(\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} + ... + \frac{1}{{{C_n}}}\)
+ Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = \frac{1}{2}C{U_0}^2 = \frac{{{Q_0}^2}}{{2C}} = \frac{{LI{{_0^{}}^2}}}{2}\)
+ Ta có hai tụ mắc nối tiếp,
=> Điện dung của bộ tụ:
\(\begin{array}{l}\frac{1}{C} = \frac{1}{{{C_1}}} + \frac{1}{{{C_2}}} = \frac{1}{{3{C_0}}} + \frac{1}{{6{C_0}}} = \frac{1}{{2{C_0}}}\\ \to C = {\rm{ }}2{C_0}\end{array}\)
+ Điện tích của bộ tụ sau khi nối với pin: \(Q = {C_B}E = 2{C_0}E = 6{C_0}\)
+ Năng lượng của mạch dao động \(W{\rm{ }} = \frac{{{Q^2}}}{{2{C_B}}} = \frac{{36C_0^2}}{{4{C_0}}} = 9{C_0}\)
+ Năng lượng của mạch sau khi nối tắt \({C_1}\): \({\rm{W}} = \frac{{U_0^2{C_2}}}{2} \Rightarrow U_0^2 = \frac{{2W}}{{{C_2}}} = \frac{{18{C_0}}}{{6{C_0}}} = 3 \Rightarrow {U_0} = \sqrt 3 \left( V \right)\)
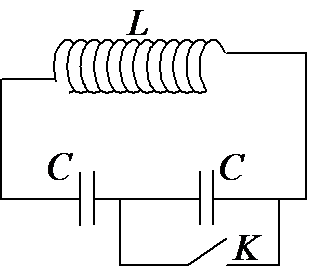
Mạch dao động điện từ lí tưởng gồm cuộn dây thuần cảm và hai tụ điện giống hệt nhau ghép nối tiếp. Hai bản của một tụ được nối với nhau bằng khóa K. Ban đầu khóa K mở. Cung cấp năng lượng cho mạch dao động thì điện áp cực đại giữa hai đầu cuộn cảm là \(8\sqrt 6 V\) . Sau đó vào đúng thời điểm dòng điện qua cuộn dây có cường độ bằng giá trị hiệu dụng thì đóng khóa K. Hiệu điện thế cực đại giũa hai đầu cuộn dây sau khi đóng khóa K:
-
A
\(12\sqrt 3 V\)
-
B
\(12 V\)
-
C
\(16 V\)
-
D
\(14\sqrt 6 V\)
Đáp án của giáo viên lời giải hay : B
+ Sử dụng biểu thức tính năng lượng của mạch: \({\rm{W}} = \dfrac{1}{2}CU_0^2\)
+ Sử dụng biểu thức tính năng lượng từ trường: \({{\rm{W}}_L} = \dfrac{1}{2}L{i^2}\)

+ Năng lượng ban đầu của mạch: \({W_0} = \dfrac{{\dfrac{C}{2}U_0^2}}{2} = \dfrac{{CU_0^2}}{4} = {\rm{ }}96C\)
+ Khi nối tắt một tụ (đóng khoá k): \({W_L} = \dfrac{{L{I^2}}}{2} = \dfrac{1}{2}\dfrac{{LI_0^2}}{2} = \dfrac{1}{2}{{\rm{W}}_0} = 48C\)
+ Năng lượng của tụ còn lại: \({{\rm{W}}_C} = \dfrac{1}{2}\left( {{{\rm{W}}_0} - {{\rm{W}}_L}} \right) = \dfrac{1}{2}\left( {96 - 48} \right)C = 24C\)
+ Năng lượng của mạch sau khi đóng khóa K : \(W{\rm{ }} = {\rm{ }}{W_L} + {\rm{ }}{W_C} \to \dfrac{{CU_{{\rm{max}}}^2}}{2} = 48C + 24C = 72C\)
\( \to U_{max}^2 = 144 \to {U_{{\rm{max}}}} = 12V\)
Một mạch dao động LC lí tưởng gồm cuộn thuần cảm L và hai tụ điện C giống nhau mắc nối tiếp. Mạch đang hoạt động thì ngay tại thời điểm nặng lượng điện trường trong tụ gấp đôi năng lượng từ trường trong cuộn cảm, một tụ bị đánh thủng hoàn toàn. Điện áp cực đại hai đầu cuộn cảm đó sẽ bằng bao nhiêu lần so với lúc đầu?
-
A
\(\dfrac{2}{3}\)
-
B
\(\dfrac{1}{3}\)
-
C
\(\dfrac{1}{{\sqrt 3 }}\)
-
D
\(\dfrac{2}{{\sqrt 3 }}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
Gọi \({U_0}\) là điện áp cực đại lúc đầu giữa hai đầu cuộn cảm cũng chính là điện áp cực đại giữa hai đầu bộ tụ; \(C\) là điện dung của mỗi tụ.
+ Năng lượng ban đầu của mạch dao động
\({{\rm{W}}_0} = \dfrac{{\dfrac{C}{2}U_0^2}}{2} = \dfrac{C}{4}U_0^2\)
Theo giả thuyết, khi năng lượng điện trường \({W_C}\) trong tụ gấp đôi năng lượng từ trường \({W_L}\) trong cuộn cảm, thì: \({W_{{C_1}}} = {W_{{C_2}}} = {W_L} = \frac{1}{3}{W_0}\)
+ Khi một tụ bị đánh thủng hoàn toàn thì năng lượng của mạch:\({\rm{W}} = \dfrac{2}{3}{{\rm{W}}_0} = \dfrac{2}{3}\dfrac{{CU_0^2}}{4} = \dfrac{{CU_0^2}}{6}\)
Mặt khác:
\(\begin{array}{l}{\rm{W}} = \dfrac{{C{U'}_0^2}}{2} \Rightarrow \dfrac{{C{U'}_0^2}}{2} = \dfrac{{CU_0^2}}{6}\\ \Rightarrow {U'}_0 = \dfrac{{{U_0}}}{{\sqrt 3 }}\end{array}\)
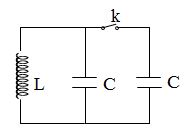
Mạch dao động điện từ gồm cuộn cảm và một bộ hai tụ điện có cùng điện dung \(C = 2,5\mu F\) mắc song song. Trong mạch có dao động điện từ tự do, hiệu điện thế cực đại giữa hai bản tụ điện là \({U_0} = 12V\). Tại thời điểm hiệu điện thế hai đầu cuộn cảm \({u_L} = 6V\) thì một tụ điện bị bong ra vì đứt dây nối. Tính năng lượng cực đại trong cuộn cảm sau đó:
-
A
\(0,27{\rm{ }}mJ\)
-
B
\(0,135{\rm{ }}mJ\)
-
C
\(0,315J\)
-
D
\(0,54{\rm{ }}mJ\)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
+ Năng lượng ban đầu của mạch dao động:
\({W_0} = \dfrac{{{C_b}U_0^2}}{2} = \dfrac{{2CU_0^2}}{2} = C{U_0}^2 = 2,{5.10^{ - 6}}144{\rm{ }} = {\rm{ }}{360.10^{ - 6}}J = {\rm{ }}0,360{\rm{ }}mJ\)
+ Năng lượng của cuộn cảm khi \({u_L} = {\rm{ }}6V\): \( \to {u_C} = {u_L}\)
\({W_C} = \dfrac{{2Cu_L^2}}{2} = {\rm{ }}C{u_L}^2 = {90.10^{ - 6}}J = 0,090mJ\)
\({W_L} = {\rm{ }}{W_0}-{\rm{ }}{W_C} = {\rm{ }}0,360{\rm{ }}-{\rm{ }}0,090{\rm{ }} = {\rm{ }}0,270{\rm{ }}mJ\)
+ Khi một tụ bị hỏng, năng lượng của mạch:
\(W{\rm{ }} = {\rm{ }}{W_L} + \dfrac{{{W_C}}}{2} = 0,270{\rm{ }} + {\rm{ }}0,045{\rm{ }} = {\rm{ }}0,315{\rm{ }}mJ\)
Do đó: \({W_{Lmax}} = {\rm{ }}W{\rm{ }} = {\rm{ }}0,315{\rm{ }}mJ\)
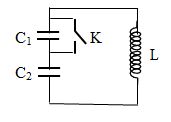
Một mạch dao động gồm cuộn thuần cảm \(L\) và hai tụ \({C_1} = 2{C_2}\) mắc nối tiếp. Mạch đang hoạt động thì ta đóng khóa \(K\) ngay tại thời điểm năng lượng trong cuộn cảm triệt tiêu. Năng lượng toàn phần của mạch sau đó sẽ:
-
A
không đổi
-
B
giảm còn \(\frac{1}{3}\)
-
C
giảm còn \(\frac{2}{3}\)
-
D
giảm còn \(\frac{4}{9}\)
Đáp án của giáo viên lời giải hay : C
Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \frac{1}{2}C{U_0}^2 = \frac{{{Q_0}^2}}{{2C}} = \frac{{LI{{_0^{}}^2}}}{2}\)
Gọi \({Q_0}\) là điện tích cực đại trong mạch
+ Năng lượng ban đầu của mạch: \({{\rm{W}}_0} = \frac{{Q_0^2}}{{2C}} = \frac{{3Q_0^2}}{{2{C_1}}} = \frac{{3Q_0^2}}{{4{C_2}}}\)
Khi năng lượng cuộn cảm triệt tiêu: \(q{\rm{ }} = {\rm{ }}{Q_0}\)
\({W_0} = {\rm{ }}{W_1} + {\rm{ }}{W_2}\) với \({W_2} = \frac{{Q_0^2}}{{2{C_2}}}\).
+ Khi đóng khóa K thi năng lượng toàn phấn của mạch \(W = {W_2} = \frac{{Q_0^2}}{{2{C_2}}}\) (2)
Từ đó suy ra \(\frac{W}{{{W_0}}} = \frac{2}{3} \to {\rm{W}} = \frac{2}{3}{{\rm{W}}_0}\)
Ăng-ten sử dụng một mạch dao động \(LC\) lý tưởng để thu sóng điện từ, trong đó cuộn dây có \(L\) không đổi, tụ điện có điện dung \(C\) thay đổi được. mỗi sóng điện từ đều tạo ra trong mạch dao động một suất điện động cảm ứng. Xem rằng các sóng điện từ có biên độ cảm ứng từ đều bằng nhau. Khi điện dung của tụ điện \({C_1} = 1\mu F\) thì suất điện động cảm ứng hiệu dụng trong mạch do sóng điện từ tạo ra là \({E_1} = 4,5\mu V\). Khi điện dung của tụ điện \({C_2} = 9\mu F\) thì suất điện động cảm ứng hiệu dụng do sóng điện từ tạo ra là:
-
A
\({E_2} = {\rm{ }}1,5\mu V\)
-
B
\({E_2} = {\rm{ }}2,25\mu V\)
-
C
\({E_2} = {\rm{ }}13,5\mu V\)
-
D
\({E_2} = 9\mu V\)
Đáp án của giáo viên lời giải hay : A
+ Viết biểu thức từ thông: \(\Phi \)
+ Suất điện động cảm ứng: \(e = - \Phi '\)
+ Vận dụng biểu thức tính tần số góc \(\omega = \frac{1}{{\sqrt {LC} }}\)
+ Sử dụng biểu thức tính biên độ của suất điện động cảm ứng: \({E_0} = {\Phi _0}\omega \)
+ Từ thông xuất hiện trong mạch \(\Phi = NBScos\omega t\)
+ Suất điện động cảm ứng xuất hiện:
\(e = - \Phi ' = NBS\omega c{\rm{os}}\left( {\omega t - \frac{\pi }{2}} \right) = E\sqrt 2 c{\rm{os}}\left( {\omega t - \frac{\pi }{2}} \right)\) với \(\omega = \frac{1}{{\sqrt {LC} }}\) tần số góc của mạch dao động
\(E = NBS\omega \) là suất điện động hiệu dụng xuất hiện trong mạch
$\frac{{{E_1}}}{{{E_2}}} = \frac{{{\omega _1}}}{{{\omega _2}}} = \sqrt {\frac{{{C_2}}}{{{C_1}}}} = 3 \to {E_2} = \frac{{{E_1}}}{3} = \frac{{4,5}}{3} = 1,5\mu V$
Một mạch dao động $LC$ lí tưởng. Ban đầu nối hai đầu cuộn cảm thuần với nguồn điện có $r = 2\Omega $ , suất điện động $E$. Sau khi dòng điện qua mạch ổn định, người ta ngắt cuộn dây với nguồn và nối nó với tụ điện thành mạch kín thì điện tích cực đại của tụ là ${4.10^{ - 6}}C$. Biết khoảng thời gian ngắn nhất kể từ khi năng lượng từ trường đạt giá trị cực đại đến khi năng lượng trên tụ bằng $3$ lần năng lượng trên cuộn cảm là $\dfrac{\pi }{6}{.10^{ - 6}}s$. Giá trị của suất điện động $E$ là:
-
A
$2 V$
-
B
$6 V$
-
C
$8 V$
-
D
$4 V$
Đáp án của giáo viên lời giải hay : C
+ Sử dụng biểu thức định luật Ôm: \(I = \dfrac{E}{{R + r}}\)
+ Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
+ Cường độ dòng điện cực đại qua mạch: \({I_0} = \dfrac{E}{r}\)
+ Năng lượng ban đầu của mạch: W0 = \(\dfrac{{LI_0^2}}{2}\) = \(\dfrac{{Q_0^2}}{{2C}}\)
+ Khi năng lượng của tụ \({{\rm{W}}_C} = 3{{\rm{W}}_L}\) => $\dfrac{{{q^2}}}{{2C}} = \dfrac{3}{4}\dfrac{{{Q^2}}}{{2C}} \to q = \dfrac{{\sqrt 3 }}{2}{Q_0}$
+ Thời gian điện tích giảm từ \({Q_0}\) đến \(\dfrac{{\sqrt 3 }}{2}{Q_0}\)
là $t = \dfrac{T}{{12}} = \dfrac{\pi }{6}{.10^{ - 6}} \to T = 2\pi {.10^{ - 6}}s$
Mặt khác:
+ Chu kì: \(T = 2\pi \sqrt {LC} = 2\pi {10^{ - 6}} \to \sqrt {LC} = {10^{ - 6}}\)
+ Cường độ dòng điện cực đại: \({I_0} = \omega {Q_0} = \dfrac{{{Q_0}}}{{\sqrt {LC} }} = \dfrac{{{{4.10}^{ - 6}}}}{{{{10}^{ - 6}}}} = 4A\)
Ta suy ra: \(E = {I_0}r = 8V\)
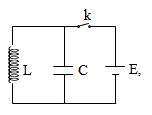
Cho mạch điện như hình vẽ bên. Cuộn dây thuần cảm có độ tự cảm $L = {4.10^{ - 3}}H$, tụ điện có điện dung $C{\rm{ }} = {\rm{ }}0,1\mu F$, nguồn điện có suất điện động $E{\rm{ }} = {\rm{ }}3mV$ và điện trở trong $r = 1\Omega $. Ban đầu khóa $k$ đóng, khi có dòng điện chạy ổn định trong mạch, ngắt khóa $k$ . Tính điện tích trên tụ điện khi năng lượng từ trong cuộn dây gấp $3$ lần năng lượng điện trường trong tụ điện?
-
A
\({3.10^{ - 8}}C\)
-
B
\({2,6.10^{ - 8}}C\)
-
C
\({6,2.10^{ - 7}}C\)
-
D
\({5,2.10^{ - 8}}C\)
Đáp án của giáo viên lời giải hay : A
+ Sử dụng biểu thức định luật ôm: $I = \dfrac{E}{{R + r}}$
+ Vận dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
+ Cường độ dòng điện cực đại qua cuộn cảm \({I_0} = {\rm{ }}\dfrac{E}{r}{\rm{ }} = {\rm{ }}3mA{\rm{ }} = {\rm{ }}{3.10^{ - 3}}A\)
+ Năng lượng từ trường bằng 3 lần năng lượng điên trường có nghĩa là:
\({{\rm{W}}_C} = \dfrac{1}{4}{{\rm{W}}_0} = \dfrac{1}{4}\dfrac{{LI_0^2}}{2}\) hay \(\dfrac{{{q^2}}}{{2C}} = \dfrac{1}{4}\dfrac{{LI_0^2}}{2} \Rightarrow q = I_0^{}\sqrt {\dfrac{{LC}}{4}} = {3.10^{ - 3}}\sqrt {\dfrac{{{{4.10}^{ - 3}}{{.10}^{ - 7}}}}{4}} = {3.10^{ - 8}}\left( C \right)\)
Một mạch dao động \(LC\) có \(L{\rm{ }} = {\rm{ }}2mH,{\rm{ }}C = 8pF\) , lấy \({\pi ^2} = 10\). Thời gian từ lúc tụ bắt đầu phóng điện đến lúc có năng lượng điện trường bằng ba lần năng lượng từ trường là:
-
A
\({2.10^{ - 7}}s\)
-
B
\({10^{ - 7}}s\)
-
C
\(\frac{{{{10}^{ - 5}}}}{{75}}s\)
-
D
\(\frac{{{{10}^{ - 6}}}}{{15}}s\)
Đáp án của giáo viên lời giải hay : D
+ Sử dụng biểu thức tính chu kì dao động : \(T = 2\pi \sqrt {LC} \)
+ Vận dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \frac{1}{2}C{U_0}^2 = \frac{{{Q_0}^2}}{{2C}} = \frac{{LI{{_0^{}}^2}}}{2}\)
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)
Ta có: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{2.10}^{ - 3}}{{.8.10}^{ - 12}}} = {8.10^{ - 7}}s\)
Đề cho: \({W_C}{\rm{ }} = 3{W_L} \to {W_L} = \frac{{{W_C}}}{3}\)
\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = {{\rm{W}}_C} + \frac{{{{\rm{W}}_C}}}{3} = \frac{4}{3}{{\rm{W}}_C}\\ \leftrightarrow \frac{{q_0^2}}{{2C}} = \frac{4}{3}\frac{{{q^2}}}{{2C}}\\ \to q = \frac{{\sqrt 3 }}{2}{q_0}\end{array}\)
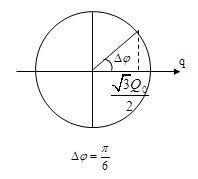
Hình vẽ cho ta góc quét : \(\Delta \varphi = \frac{\pi }{6}\)
Mặt khác, ta có : \(\Delta \varphi = \omega \Delta t \to \Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{\pi }{6}}}{{\frac{{2\pi }}{T}}} = \frac{T}{{12}}\)
\(\Delta t = \frac{T}{{12}} = \frac{{{{8.10}^{ - 7}}}}{{12}} = \frac{2}{3}{10^{ - 7}} = \frac{1}{{15}}{10^{ - 6}}s\)
Trong mạch dao động LC có điện trở thuần không đáng kể, chu kỳ dao động của mạch là \(T{\rm{ }} = {\rm{ }}{10^{ - 6}}s\), khoảng thời gian ngắn nhất để năng lượng điện trường lại bằng năng lượng từ trường :
-
A
\({2,5.10^{ - 5}}s\)
-
B
\({10^{ - 6}}s\)
-
C
\({5.10^{ - 7}}s\)
-
D
\({2,5.10^{ - 7}}s\)
Đáp án của giáo viên lời giải hay : D
+ Vận dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)
Đề cho: \({W_C} = {W_L}\)
W = WC + WL = \(\dfrac{{{q^2}}}{{2C}}\) + \(\dfrac{{L{i^2}}}{2}\)
<=>\(\dfrac{{{q_0}^2}}{{2C}}\) =\(\dfrac{{{q^2}}}{{2C}}\) +\(\dfrac{{{q^2}}}{{2C}}\)
<=> \(q = \dfrac{{\sqrt 2 }}{2}{q_0}\)
Hình vẽ vòng lượng gíác cho ta góc quét từ lúc năng lượng điện trường cực đại đến năng lượng điện trường bàng năng lượng từ rường là: \(\Delta \varphi = \dfrac{\pi }{4}\)
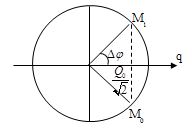
Vậy từ lúc năng lượng điện trường bằng năng lượng từ trường đến lúc năng lượng điện trường bàng năng lượng từ trường lần kế tiếp là:
\(\Delta \varphi ' = \dfrac{\pi }{2}\) ( xem hình vẽ từ M0 đến M1)
Ứng với thời gian \(t = \dfrac{T}{4} = \dfrac{{{{10}^{ - 6}}}}{4} = {2,5.10^{ - 7}}s\)
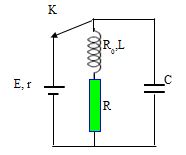
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E = 12V\) điện trở trong \(r = 1\Omega \), tụ có điện dung \(C = 100\mu F\), cuộn dây có hệ số tự cảm \(L = 0,2H\) và điện trở là \({R_0} = 5\Omega \); điện trở \(R = 18\Omega \). Ban đầu K đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá K. Tính nhiệt lượng tỏa ra trên điện trở \(R\) trong thời gian từ khi ngắt K đến khi dao động trong mạch tắt hoàn toàn?
-
A
25 mJ
-
B
28,45 mJ
-
C
24,74 mJ
-
D
5,175mJ
Đáp án của giáo viên lời giải hay : C
+ Vận dụng biểu thức định luật Ôm: \(I = \dfrac{E}{{R + r}}\)
+ Sử dụng biểu thức tính năng lượng điện từ
+ Vận dụng biểu thức tính nhiệt lượng: \(Q = {I^2}Rt\)
+ Khi K đóng \(I = \dfrac{E}{{\left( {R{\rm{ }} + r + {R_0}} \right)}} = \dfrac{{12}}{{\left( {{\rm{ }}18 + 1 + 5} \right)}} = 0,5A\)
+ Điện áp \(2\) đầu tụ \(C\) lúc đầu: \({U_0} = I\left( {R + {R_0}} \right) = 0,5.23 = 11,5V\)
+ Năng lượng lúc đầu của mạch: \(W = \dfrac{{CU_0^2}}{2} + \dfrac{{LI_0^2}}{2} = \dfrac{{{{10}^{ - 4}}.11,5_{}^2}}{2} + \dfrac{{0,2.0,5_{}^2}}{2} = {0,66125.10^{ - 2}} + 0,025 = 0,0316125J\) .
Năng lượng tỏa ra trên \(R\) và \({R_0}\) tỉ lệ thuận với điện trở: $\dfrac{{{Q_R}}}{{{Q_{{R_0}}}}} = \dfrac{R}{{{R_0}}}$
Khi mạch tắt hoàn toàn thì năng lượng \(W\) chuyển thành nhiệt lượng tỏa ra trên \(R\) và \({R_0}\) nên ta có: $Q_R+Q_{R_0}=W$
=> Nhiệt lượng tỏa ra trên $R$ là:
\(Q = \dfrac{{18}}{{23}}W = \dfrac{{18}}{{23}}.0,0316125 = 0,024740217J \approx 0,02474J = 24,74{\rm{ }}mJ\)
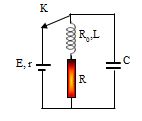
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E = 24V,r = 1\Omega \), tụ điện có điện dung \(C = 100\mu F\), cuộn dây có hệ số tự cảm \(L{\rm{ }} = {\rm{ }}0,2H\) và điện trở \({R_0} = 5\Omega \), điện trở \(R = 18\Omega \). Ban đầu khoá K đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá K. Nhiệt lượng toả ra trên điện trở R trong thời gian từ khi ngắt khoá k đến khi dao động trong mạch tắt hoàn toàn.
-
A
98,96 mJ
-
B
24,74 mJ
-
C
126,45 mJ
-
D
31,61 mJ
Đáp án của giáo viên lời giải hay : A
+ Vận dụng biểu thức định luật Ôm: \(I = \dfrac{E}{{R + r}}\)
+ Sử dụng biểu thức tính năng lượng điện từ
+ Vận dụng biểu thức tính nhiệt lượng: \(Q = {I^2}Rt\)
Cách 1:
+ Cường độ dòng điện qua mạch trước khi mở khóa K: \({I_0} = \dfrac{E}{{R + {R_0} + r}} = \dfrac{{24}}{{24}} = 1A\)
+ Điện áp giữa hai bản cực tụ điện \(U{\rm{ }} = {\rm{ }}I\left( {R{\rm{ }} + {\rm{ }}{R_0}} \right){\rm{ }} = {\rm{ }}23{\rm{ }}V\)
+ Năng lượng của mạch dao động sau khi ngắt khóa K:
\({{\rm{W}}_0} = \dfrac{{LI_0^2}}{2} + \dfrac{{C{U^2}}}{2} = 0,1J + 0,02645J = 0,12645J = 126,45mJ\)
+ Trong thời gian từ khi ngắt khoá K đến khi dao động trong mạch tắt hoàn toàn, năng lượng này biến thành nhiệt lượng tỏa ra trên điện trở \(R\) và trên \({R_0}\) của cuộn dây
+ Nhiệt lượng tỏa ra trên điện trở \(R\) là: \({Q_R} = \dfrac{{{{\rm{W}}_0}}}{{R + {R_0}}}R = \dfrac{{126,45}}{{23}}.18 = 98,96mJ\)
Cách 2:
Ta có:
\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}.L{.1^2} + \dfrac{1}{2}.C.{\left( {24 - 1} \right)^2} = 0,12645J\\ = > {Q_R} = \dfrac{{18}}{{23}}.0,12645 = 98,96mJ\end{array}\)
Nếu hai đầu đoạn mạch gồm cuộn cảm thuần L mắc nối tiếp với điện trở thuần \(R = 1\,\,\Omega \) vào hai cực của nguồn điện một chiều có suất điện động và điện trở trong r không đổi thì trong mạch có dòng điện không đổi cường độ I. Dùng nguồn điện này để nạp điện cho một tụ điện có điện dung \(C = {2.10^{ - 6}}\,\,F\). Khi điện tích trên tụ điện đạt giá trị cực đại, ngắt tụ điện khỏi nguồn rồi nối tụ điện với cuộn cảm thuần L thành một mạch dao động thì trong mạch có dao động điện từ tự do với chu kì bằng \(\pi {.10^{ - 6}}\,\,s\) và cường độ dòng điện cực đại bằng 6I. Giá trị của r bằng
-
A
2 Ω
-
B
0,25 Ω
-
C
0,5 Ω
-
D
1 Ω
Đáp án của giáo viên lời giải hay : C
Định luật Ôm cho toàn mạch: \(I = \dfrac{E}{{r + R}}\)
Chu kì của mạch dao động điện từ tự do: \(T = 2\pi \sqrt {LC} \)
Định luật bảo toàn năng lượng cho mạch dao động điện từ tự do: \(\dfrac{1}{2}L{I_0}^2 = \dfrac{1}{2}C{U_0}^2\)
Khi mắc cuộn cảm thuần L và điện trở R với nguồn, cường độ dòng điện trong mạch là:
\(I = \dfrac{E}{{r + R}} \Rightarrow E = I\left( {r + R} \right)\)
Khi mắc tụ điện với cuộn cảm thành mạch dao động điện từ tự do, chu kì của mạch là:
\(T = 2\pi \sqrt {LC} \Rightarrow \pi {.10^{ - 6}} = 2\pi .\sqrt {L{{.2.10}^{ - 6}}} \Rightarrow L = 1,{25.10^{ - 7}}\,\,\left( H \right)\)
Điện áp cực đại giữa hai đầu tụ điện là: \({U_0} = E = I.\left( {r + R} \right)\)
Ta có định luật bảo toàn năng lượng trong mạch dao động điện từ tự do:
\(\begin{array}{l}\dfrac{1}{2}L{I_0}^2 = \dfrac{1}{2}C{U_0}^2 \Rightarrow L{\left( {6I} \right)^2} = C.{I^2}{\left( {r + R} \right)^2}\\ \Rightarrow 1,{25.10^{ - 7}}.36{I^2} = {2.10^{ - 6}}{I^2}.{\left( {r + 1} \right)^2} \Rightarrow r = 0,5\,\,\left( \Omega \right)\end{array}\)
