32.1
Em hãy viết chương trình nhập một họ tên đầy đủ từ bàn phím, ví dụ "Nguyễn Thị Mai Hương", sau đó tách riêng phần tên, họ, đệm và thông báo ra màn hình.
Phương pháp giải:
Em đã biết cách tách phần họ và tên của một xâu kí tự họ tên đầy đủ. Bài tập này yêu cầu tách thêm phần đệm, tức là phần nằm giữa tên và họ ra. Việc tách này khá đơn giản bằng cách sử dụng phương thức join() của xâu kí tự. Xâu kí tự họ tên gốc trước tiên được tách thành một dãy bằng hàm split(). Sau khi lấy phần họ, tên, phần đệm sẽ được lấy ra bằng lệnh sau:
dem = " ".join(slist[1:n-1])
Trong đó slist là dãy đã được tách ra từ xâu kí tự họ tên đầy đủ, n là độ dài của xâu slist.
Lời giải chi tiết:
Chương trình chính có thể như sau:
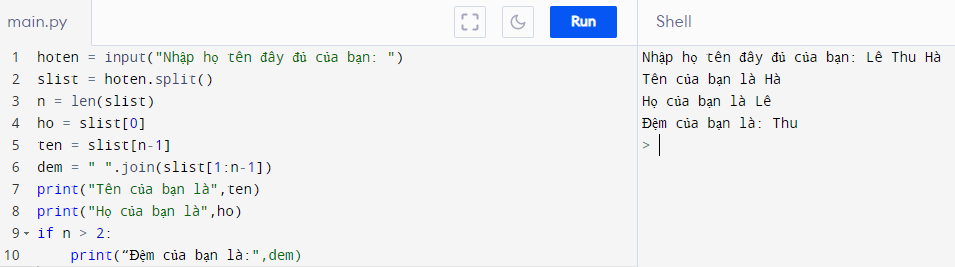
32.2
Nhà nước quản lí lượng tiêu thụ điện được thống kê theo tháng. Tháng được gọi là đột biến nếu sản lượng tiêu thụ của tháng đó lớn hơn cả tháng trước và sau tháng đó. Dữ liệu sản lượng tiêu thụ điện hàng tháng được cho bởi dãy các số, ví dụ:
a[0], a[1],….., a[N-1].
Cần tìm và liệt kê các chỉ số và giá trị a[i] sao cho a[i] tương ứng với tháng đột biến.
Yêu cầu nhập dữ liệu sản lượng điện tiêu thụ từ bàn phím trên một hàng có N số, mỗi số cách nhau bởi dấu cách. Chương trình cần in ra dãy các tháng (bằng chỉ số dãy) và sản lượng tiêu thụ đột biến của tháng đó.
Phương pháp giải:
Vận dụng kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình chính có thể như sau:

32.3
Bài toán đếm số lần lặp của một mẫu xâu trong xâu gốc như sau: Cho trước xâu gốc S và một xâu mẫu str. Yêu cầu cần tìm số lần lặp của xâu mẫu str trong xâu gốc S. Có hai kiểu tìm số lần lặp:
- Tìm số lần lặp xâu con có thể chồng lấn lên nhau.
- Tìm số lần lặp không chồng lấn của xâu con.
Ví dụ nếu xâu gốc là "12121341212100", xâu con mẫu là "121" thì:
- Số lần lặp có chồng lấn của str trong S là 4 lần.
- Số lần lặp không chồng lấn của str trong S là 2 lần.
Bài toán như sau: Cho trước các xâu kí tự S và str, hãy tìm số lần lặp không chồng lấn của xâu str trong xâu S.
Phương pháp giải:
Vận dụng kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình chính có thể như sau:
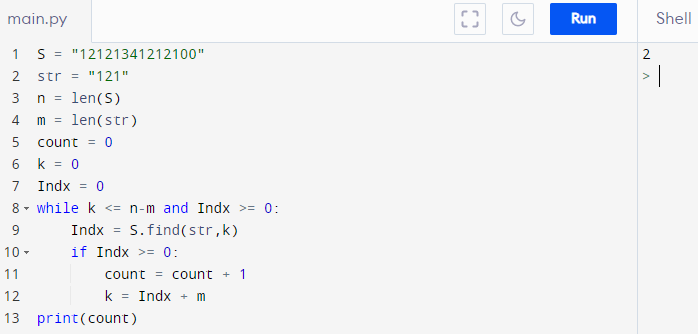
32.4
Cho trước dãy số. Yêu cầu cần tìm ra một dãy con liên tục có độ dài lớn nhất bao gồm các số bằng nhau. Ví dụ với dãy: 1, 1, 2, 3, 0, 0, 0, 7, 10, 10, 5, 1, 1, 6 thì cần đưa ra thông báo:
Dãy con bằng nhau có độ dài lớn nhất là 0, 0, 0 bắt đầu từ chỉ số 4.
Dãy số gốc gồm các số nguyên được nhập trên một dòng từ bàn phím, chương trình cần đưa ra thông báo như trên.
Phương pháp giải:
Vận dụng kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình chính có thể như sau:
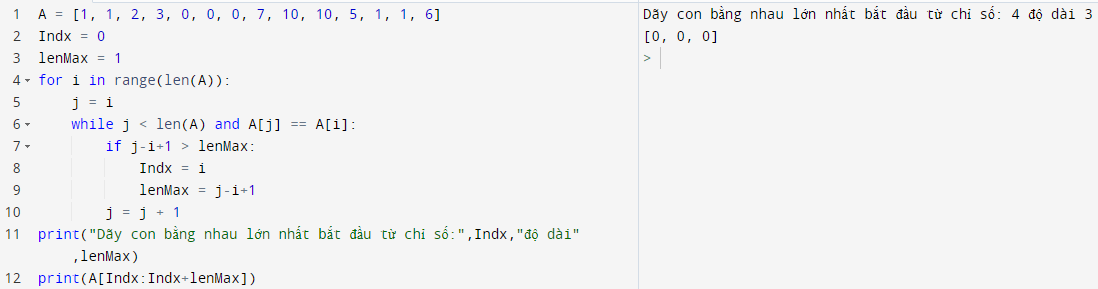
32.5
Trong các phần mềm bảng tính điện tử, dữ liệu ngày tháng được coi là số ngày tính từ ngày 1-1-1990. Viết chương trình nhập số tự nhiên n từ bàn phím và tính xem số đó ứng với ngày, tháng, năm nào.
Phương pháp giải:
Vận dụng kiến thức đã học để viết chương trình
Lời giải chi tiết:
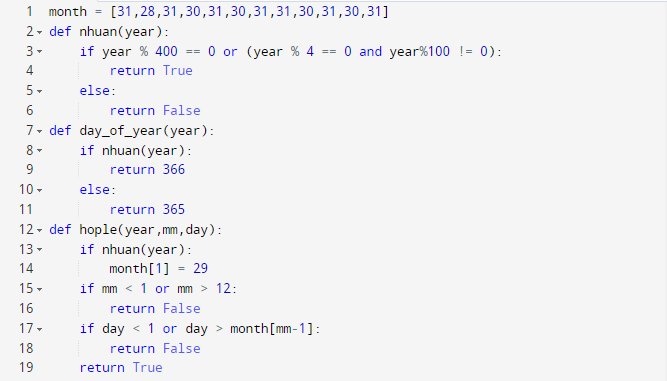
Chương trình chính có thể như sau:
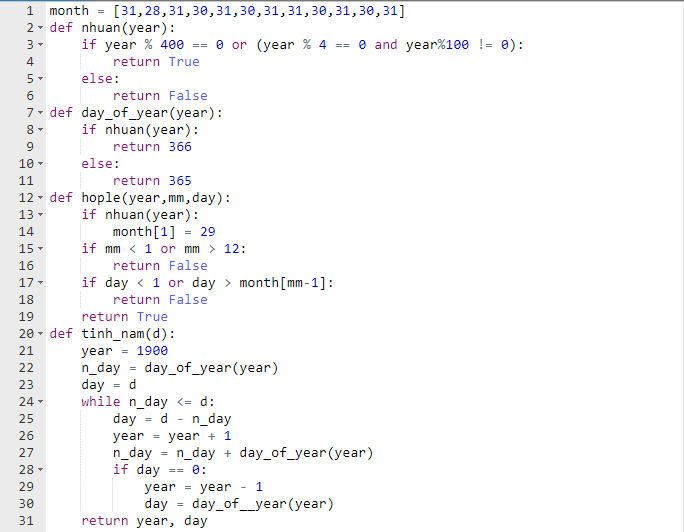
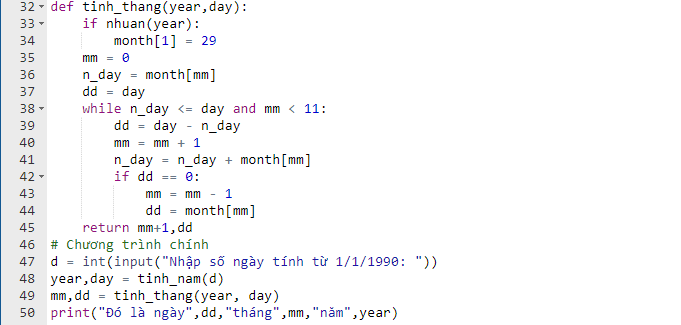
32.6
Trong các phần mềm bảng tính điện tử, dữ liệu ngày tháng được coi là số ngày tính từ ngày 1-1-1990.
Nhập thời gian theo khuôn dạng ngày-tháng-năm (ví dụ 8-10-2021), tính giá trị của ngày này theo cách lưu trữ của phần mềm bảng tính điện tử.
Phương pháp giải:
Vận dụng kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình chính có thể như sau:

32.7
Viết chương trình nhập số n, sau đó nhập danh sách học sinh trong lớp với đầy đủ họ, đệm, tên. Sau đó cần sắp xếp học sinh trong lớp theo thứ tự từ điền (tức là thứ tự của bảng chữ cái trong bảng mã Unicode). Đưa kết quả ra màn hình.
Phương pháp giải:
Vận dụng kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình chính có thể như sau:

Lưu ý: Hàm sap_xep(A) sẽ trả lại dãy đã được sắp xếp tăng dần của A, bản thân dãy A không thay đổi.
32.8
Mở rộng bài tập trên như sau:
- Việc sắp xếp thứ tự phải ưu tiên tính theo tên trước, rồi đến họ, rồi đến đệm.
- Sắp xếp theo thứ tự của bảng chữ cái tiếng Việt.
Chú ý: Bảng chữ cái tiếng Việt (bao gồm cả dấu thanh) được sắp xếp theo thứ tự sau: AÀÁẢÃẠĂẰẮẲẴẶÂẦẤẪẬBCDĐEÈÉẺẼẸÊỀẾỂỄỆGHIÌÍỈĨỊJKLMNOÒÓỎÕỌÔỒỐỔỖỘƠỜỚỞỠỢPQRSTUÙÚỦŨỤƯ ỪỨỬỮỰVXYỲÝỶỸỴ.
Phương pháp giải:
Dựa vào kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình có thể viết như sau:

32.9
Nếu n là hợp số thì dễ thấy n phải có ước số nguyên tố nhỏ hơn hoặc bằng . Viết chương trình tối ưu hoá hơn nhiệm vụ 1, bài 31, theo cách sau: để tìm ước số nguyên tố nhỏ nhất chỉ cần tìm trong các số 2, 3,... Nếu trong dãy trên không tìm thấy ước của n thì kết luận ngay n là số nguyên tố.
Phương pháp giải:
Dựa vào kiến thức đã học để viết chương trình
Lời giải chi tiết:
Chương trình có thể viết như sau:

32.10
Bài toán mô tả đường bay của hòn đá khi được ném lên.
Viết chương trình mô tả bài toán chuyển động của hòn đá khi được ném lên từ một vị trí ban đầu. Yêu cầu tính toán là hòn đá di chuyển trong điều kiện lí tường không có lực cản không khí và ma sát. Bài toán có thể lấy mô hình hòn đá, hoặc quả lựu đạn, hoặc quả tên lửa được bắn ra,...
Các thông tin ban đầu cần nhập từ bàn phím:
- Góc ném hòn đá: a (tính theo độ, yêu cầu 0 < a < 90).
- Vị trí (độ cao) khi ném hòn đá: h (tính theo mét, yêu cầu h > 0).
- Độ lớn của lực (vận tốc) ném: V (tính theo m/s, yêu cầu v > 0).
Các thông tin cần tính toán để đưa kết quả ra:
- Khoảng cách ném xa của hòn đá (tính từ vị trí ném).
- Độ cao cực đại của hòn đá.
- Thời gian di chuyển của hòn đá tính từ khi bắt đầu ném cho đến khi chạm đất
Phương pháp giải:
Bài toán này nằm trong Chương trình môn Vật lí 10, phần chuyển động ném xiên của vật thể.
Lời giải chi tiết:
Quan sát hình sau. Hòn đá được ném lên từ vị trí A có độ cao h với góc ném a và vận tốc góc v. Quỹ đạo chuyển động của hòn đá sẽ có dạng parabol như trong Hình 32.1. Hòn đá sẽ lên đỉnh cao nhất tại c và sau đó chạm đất tại vị trí B. Em cần tính ba thông số H, T, L như sau:
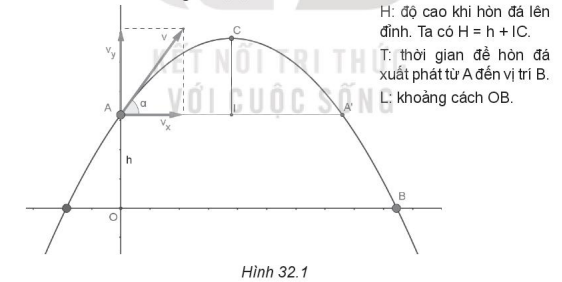
Sơ lược cách tính các tham số H, T, L.
Lực ném v sẽ phân tích thành 2 lực: lực thẳng đứng vy và lực ngang vx. Ta có công thức:
vx = v.cos(a), vy = v.sin(d) (1)
Phương trình tham số theo thời gian t của quỹ đạo hòn đá chuyển động như sau:
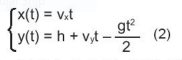
Thời gian t trong công thức (2) tính từ 0, tức là từ điểm A. g = 9.8 là trọng lực Trái Đất.
Để tính thời gian T chúng ta giải phương trình y(t) = 0 trong công thức (2). Đây là phương trình bậc hai với t. T chính là nghiệm dương của phương trình này. Khoảng cách L dễ dàng tính được theo công thức L = vxT.
Để tính độ cao H thì khó hơn.
Thời gian để hòn đá bay đến điểm A’ được tính như sau:
y(t) = h, tức là vyt - = 0, từ đó suy ra t = 2vy/g. Thời gian đi đến đỉnh C bằng một nửa thời gian đến A, vậy suy ra thời gian đạt đỉnh cao nhất là:
t= vy/g = v.sin(a)/g (3)
Từ công thức (3) dễ dàng tính được độ cao IC, từ đó tính được H.
Từ các phân tích trên chúng ta sẽ tính được các công thức sau cho T, H và L.

Để tính theo các công thức (4), (5), (6) cần sử dụng các hàm số toán học như sin, cosin, hàm tính căn bậc hai. Các hàm toán học không có sẵn trong Python mà có trong một module độc lập bên ngoài, module math. Muốn sử dụng các hàm số này chúng ta cần đưa lệnh sau vào chương trình (ở dòng lệnh đầu tiên).
from math import <danh sách các hàm>
Muốn dùng tất cả các hàm có trong module math (hay bất kì module nào khác) chúng ta dùng lệnh: from math import *
Các hàm lượng giác sin(a), cos(a) trong Python quy định tham số góc đầu vào không tính theo độ, mà theo độ đo radian. Do vậy chúng ta cần thêm một hàm số nữa là hàm radians() dùng để chuyển số đo từ độ sang radian.
Vậy chương trình sẽ cần các hàm toán học sau.
from math import sqrt, radians, sin, cos
Chương trình cần được tạo với tên flyingrocket.py và phần nội dung chính mô tả ba hàm số Timing(), Height() và Length(). Các hàm này có tham số đầu vào là v, alpha, h và có giá trị trả lại chính là T, H, L mà chúng ta cần tìm.

