Đề bài
Phần I: Trắc nghiệm (4 điểm).
Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1. Tập hợp số tự nhiên khác 0 được kí hiệu là:
A. \({\mathbb{N}^*} = \left\{ {0;1;3;5;...} \right\}\) B. \({\mathbb{N}^*} = \left\{ {1;2;3;4;...} \right\}\) C. \({\mathbb{N}^*} = \left\{ {0;1;2;3;...} \right\}\) D. \({\mathbb{N}^*} = \left\{ {0;1;5} \right\}\)
Câu 2. Kết quả của phép tính: \({8^2}{.2^3}\) là:
A. \({2^5}\) B. \({2^9}\) C. \({2^{18}}\) D. \({2^{12}}\)
Câu 3. Trong các số sau đây, số nào chia hết cho \(3\) nhưng không chia hết cho \(9\)?
A. \(900\) B. \(180\) C. \(93\) D. \(729\)
Câu 4. Có bao nhiêu ước chung của \(120\) và \(400\)?
A. \(10\) B. \(4\) C. \(5\) D. \(8\)
Câu 5. Cho bốn số nguyên \(a,b,c\) và \(d\). Khẳng định nào dưới đây là đúng?
A. \(\left( {a + b} \right) - \left( {c - d} \right) = a + b + c - d\) B. \(\left( {a + b} \right) - \left( {c - d} \right) = a + b - c + d\)
C. \(\left( {a + b} \right) - \left( {c - d} \right) = a + b - c - d\) D. \(\left( {a + b} \right) - \left( {c - d} \right) = a + b + c + d\)
Câu 6. Một tòa nhà có \(12\) tầng và \(3\) tầng hầm (tầng trệt được đánh số là tầng \(0\)), hãy dùng phép cộng các số nguyên để diễn tả tình huống sau: Một thang máy đang ở tầng số \(3\), nó đi lên \(7\) tầng và sau đó đi xuống \(12\) tầng. Hỏi cuối cùng thang máy dừng lại ở tầng mấy?
A. Tầng hầm 2 B. Tầng 2 C. Tầng trệt D. Tầng 10
Câu 7. Hình vẽ bên có bao nhiêu tam giác đều?
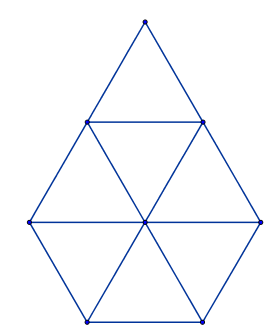
A. \(6\) B. \(7\) C. \(8\) D. \(9\)
Câu 8. Cho biểu đồ cột biểu diễn số dân của các tỉnh khu vực Tây Nguyên năm 2019:
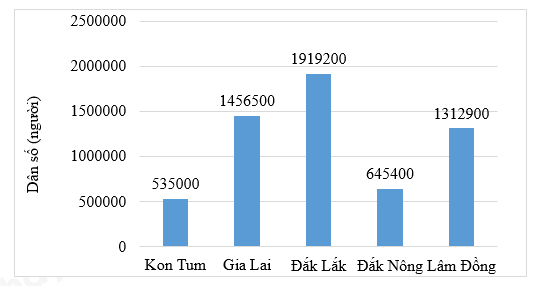
Trong các tỉnh ở khu vực Tây Nguyên, tỉnh nào có dân số nhiều nhất?
A. Kon Tum B. Gia Lai C. Đắk Lắk D. Lâm Đồng
Câu 9. Một chiếc khăn trải bàn có thêu một hình thoi ở giữa. Tính diện tích hình thoi biết rằng 2 đường chéo của nó bằng \(6dm\) và \(3dm.\)
A. \(18\,d{m^2}\) B. \(9\,d{m^2}\) C. \(12\,d{m^2}\) D. \(24\,d{m^2}\)
Câu 10. Cho bảng dữ liệu về học lực của các bạn học sinh lớp 6A và lớp 6B:
|
Học lực Lớp |
Giỏi |
Khá |
Trung bình |
Yếu |
|
6A |
\(13\) |
\(16\) |
\(9\) |
\(2\) |
|
6B |
\(9\) |
\(18\) |
\(10\) |
\(5\) |
Để biểu diễn dữ liệu của bảng trên ta có thể sử dụng biểu đồ nào sau đây?
A. Biểu đồ hình quạt B. Biểu đồ ô vuông C. Biểu đồ tranh D. Biểu đồ cột kép
Phần II. Tự luận (6 điểm):
Bài 1. (1,0 điểm) Thực hiện phép tính:
a) \(25.69 + 31.25 - 150\) b) \(198:\left[ {130 - {{\left( {27 - 19} \right)}^2}} \right] + {2021^0}\)
Bài 2. (1,0 điểm) Tìm \(x\), biết:
a) \(140:\left( {x - 8} \right) = 7\) b) \({4^{x + 3}} + {4^x} = 1040\)
Bài 3. (1,5 điểm) Số học sinh tham quan của một trường khoảng từ 1200 đến 1500 em. Nếu thuê xe 30 chỗ thì thừa 21 chỗ, nếu thuê xe 35 chỗ thì thừa 26 chỗ, nếu thuê xe 45 chỗ thì thiếu 9 ghế. Hỏi có tất cả bao nhiêu học sinh đi tham quan?
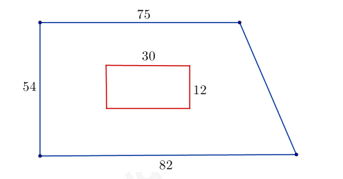
Bài 4. (2 điểm) Một trại chăn nuôi có bãi cỏ bao quanh dạng hình thang vuông với kích thước như hình vẽ (đơn vị \(m\)).
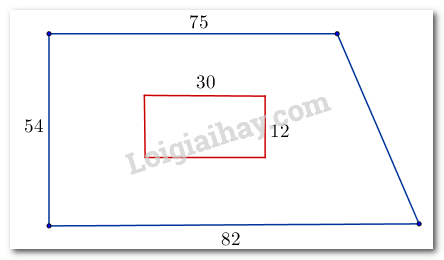
a) Tính diện tích của bãi cỏ.
b) Cần bao nhiêu túi hạt giống để gieo hết bãi cỏ biết rằng một túi hạt giống cỏ gieo vừa đủ trên \(120{m^2}\) đất?
Bài 5. (0,5 điểm) Tìm số tự nhiên \(x,y,z\) biết: \(x \le y \le z\) và \({2^x} + {3^y} + {5^z} = 156\).
Lời giải
Phần I: Trắc nghiệm
|
1. C |
2. B |
3. C |
4. D |
5. B |
6. A |
7. C |
8. C |
9. B |
10. D
|
Câu 1
Phương pháp:
Sử dụng định nghĩa tập hợp số tự nhiên khác \(0\)
Cách giải:
Tập hợp số tự nhiên khác \(0\) là: \({\mathbb{N}^*} = \left\{ {1;2;3;4;...} \right\}\).
Chọn B.
Câu 2
Phương pháp:
Vận dụng kiến thức nhân hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\) \(\left( {m,n \in \mathbb{N}} \right)\)
Sử dụng kết quả: \({\left( {{a^m}} \right)^n} = {a^{m.n}}\)
Cách giải:
Ta có: \({8^2}{.2^3} = {\left( {{2^3}} \right)^2}{.2^3} = {2^6}{.2^3} = {2^{6 + 3}} = {2^9}\)
Chọn B.
Câu 3
Phương pháp:
Sử dụng dấu hiệu chia hết cho \(3\) và \(9\).
Cách giải:
Ta có:
\(9 + 0 + 0 = 9 \vdots 3\) và \( \vdots 9\), suy ra \(900 \vdots 3;900 \vdots 9\).
\(1 + 8 + 0 = 9 \vdots 3\) và \( \vdots 9\), suy ra \(180 \vdots 3;180 \vdots 9\).
\(9 + 3 = 12 \vdots 3\) nhưng \(9 + 3 = 12\cancel{ \vdots }9\), suy ra \(93 \vdots 3;93\cancel{ \vdots }9\).
\(7 + 2 + 9 = 18 \vdots 3\) và \( \vdots 9\), suy ra \(729 \vdots 3;729 \vdots 9\).
Chọn C.
Câu 4
Phương pháp:
Tìm ước chung thông qua ước chung lớn nhất của hai số tự nhiên.
Cách giải:
Ta có:
Suy ra ƯCLN\(\left( {120,400} \right) = {2^3}.5 = 8.5 = 40\) \( \Rightarrow \)ƯC\(\left( {120,400} \right) = \)Ư\(\left( {40} \right) = \left\{ {1;2;4;5;8;10;20;40} \right\}\).
Vậy có \(8\) ước chung của \(120\) và \(400\).
Chọn D.
Câu 5
Phương pháp:
Vận dụng quy tắc bỏ dấu ngoặc khi thực hiện phép tính.
Cách giải:
Ta thực hiện phép tính bỏ ngoặc có dấy “–” ở trước: \(\left( {a + b} \right) - \left( {c - d} \right) = a + b - c + d\)
Chọn B.
Câu 6
Phương pháp:
Căn cứ vào yêu cầu đề bài, phân tích và đưa bài toán về thực hiện phép cộng với các số nguyên cho trước.
Cách giải:
Sau khi lên \(7\) tầng và xuống \(12\) thì thang máy dừng lại ở tầng:
\(3 + 7 + \left( { - 12} \right) = - 2\)
Vậy thang máy dừng lại ở tầng hầm số \(2\).
Chọn A.
Câu 7
Phương pháp:
Nhận biết được hình tam giác đều.
Cách giải:
- Có 7 tam giác đều cạnh 1.
- Có 1 tam giác đều cạnh 2.
Vậy có \(7 + 1 = 8\) (tam giác đều)
Chọn C.
Câu 8
Phương pháp:
Quan sát biểu đồ để xác định dân số của khu vực Tây Nguyên và so sánh.
Cách giải:
Quan sát biểu đồ ta thấy:
Kon Tum: 535 000 người
Gia Lai: 1 456 500 người
Đắk Lắk: 1 919 200 người
Đắk Nông: 645 400 người
Lâm Đồng: 1 312 900 người
Vậy tỉnh Đắk Lắk có số dân nhiều nhất.
Chọn C.
Câu 9
Phương pháp:
Vận dụng công thức tính diện tích hình thoi có độ dài hai đường chéo lần lượt là \(m,n\) là \(S = \dfrac{1}{2}m.n\)
Cách giải:
Diện tích của hình thoi là: \(\dfrac{{6.3}}{2} = 9\left( {d{m^2}} \right)\)
Chọn B.
Câu 10
Phương pháp:
Sử dụng lý thuyết biểu đồ cột kép.
Cách giải:
Để biểu diễn học lực của học sinh lớp 6A, 6B ta có thể sử dụng biểu đồ cột kép.
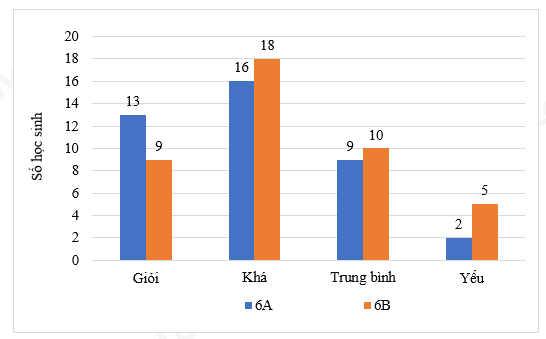
Chọn D.
Phần II: Tự luận
Bài 1
Phương pháp:
a) Thực hiện nhóm các số với nhau để tạo thành các số tròn chục, tròn trăm,… để thuận tiện tính toán
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Biểu thức có ngoặc, ta thực hiện theo thứ tự: \(\left( {\,\,\,} \right) \to \left[ {\,\,\,} \right] \to \left\{ {\,\,\,} \right\}\)
Vận dụng quy tắc bỏ ngoặc.
Cách giải:
|
a) \(25.69 + 31.25 - 150\) \(\begin{array}{l} = 25.\left( {69 + 31} \right) - 150\\ = 25.100 - 150\\ = 2500 - 150\\ = 2350\end{array}\) |
b) \(198:\left[ {130 - {{\left( {27 - 19} \right)}^2}} \right] + {2021^0}\) \(\begin{array}{l} = 198:\left( {130 - {8^2}} \right) + 1\\ = 198:\left( {130 - 64} \right) + 1\\ = 198:66 + 1\\ = 3 + 1\\ = 4\end{array}\) |
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số tự nhiên.
b) Vận dụng kiến thức lũy thừa với số mũ tự nhiên
Hai lũy thừa cùng cơ số bằng nhau khi số mũ của chúng bằng nhau.
Cách giải:
|
a) \(140:\left( {x - 8} \right) = 7\) \(\begin{array}{l}x - 8 = 140:7\\x - 8 = 20\\x = 20 + 8\\x = 28\end{array}\) Vậy \(x = 28\) |
b) \({4^{x + 3}} + {4^x} = 1040\) \(\begin{array}{l}{4^x}{.4^3} + {4^x} = 1040\\{4^x}.\left( {{4^3} + 1} \right) = 1040\\{4^x}.65 = 1040\\{4^x} = 16\\{4^x} = {4^2}\\x = 2\end{array}\) Vậy \(x = 2\). |
Bài 3
Phương pháp:
Gọi số học sinh đi tham quan là \(x\,\,\left( {x \in {\mathbb{N}^*},\,\,1200 \le x \le 1500} \right)\)
Từ đề bài, suy ra \(\left( {x + 9} \right) \in {\rm{BC}}\left( {30;35;45} \right)\)
Áp dụng các bước tìm bội chung nhỏ nhất, tìm được \({\rm{BCNN}}\left( {30;35;45} \right)\), suy ra \({\rm{BC}}\left( {30;35;45} \right)\)
Kết hợp điều kiện và đưa ra kết luận.
Cách giải:
Gọi số học sinh đi tham quan là \(x\,\,\left( {x \in {\mathbb{N}^*},\,\,1200 \le x \le 1500} \right)\)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}\left( {x - 21} \right)\,\, \vdots \,\,30\\\left( {x - 26} \right)\,\, \vdots \,\,35\\\left( {x + 9} \right)\,\, \vdots \,\,45\end{array} \right.\,\, \Rightarrow \left\{ \begin{array}{l}\left( {x - 21 + 30} \right) = \left( {x + 9} \right)\,\, \vdots \,\,30\\\left( {x - 26 + 35} \right) = \left( {x + 9\,} \right)\, \vdots \,\,35\\\left( {x + 9} \right)\,\, \vdots \,\,45\end{array} \right.\)
\( \Rightarrow \left( {x + 9} \right) \in {\rm{BC}}\left( {30;35;45} \right)\)
Ta có: \(\left\{ \begin{array}{l}30 = 2.3.5\\35 = 5.7\\45 = {3^2}.5\end{array} \right. \Rightarrow {\rm{BCNN}}\left( {30;35;45} \right) = {2.3^2}.5.7 = 630\)
\( \Rightarrow \left( {x + 9} \right) \in {\rm{BC}}\left( {630} \right) = \left\{ {0;630;1260;...} \right\}\)
\( \Rightarrow x \in \left\{ {621;1251;...} \right\}\)
Vì \(1200 \le x \le 1500 \Rightarrow x = 1251\)
Vậy có 1251 học sinh đi tham quan.
Bài 4
Phương pháp:
a) Sử dụng công thức tính diện tích hình chữ nhật có độ dài hai cạnh lần lượt là \(a,b\) thì \(S = a.b\), tính được diện tích của trại chăn nuôi.
Sử dụng công thức tính diện tích hình thang vuông có độ dài hai đáy là \(a,b\) và chiều cao tương ứng với đáy \(a\) là \(h\) thì \(A = \dfrac{{\left( {a + b} \right).h}}{2}\)
\( \Rightarrow \) Diện tích của bãi cỏ = diện tích của hình thàng vuông – diện tích của trại chăn nuôi.
b) Thực hiện phép chia, so sánh và đưa ra kết luận.
Cách giải:
a) Diện tích của trại chăn nuôi là: \(30.12 = 360\left( {{m^2}} \right)\)
Diện tích của hình thang vuông là: \(\dfrac{{\left( {75 + 82} \right).54}}{2} = 4239\left( {{m^2}} \right)\)
Diện tích của bãi cỏ là: \(4239 - 360 = 3879\left( {{m^2}} \right)\)
b) Ta có: \(3879:120 = 32\) (dư 39)
Vậy cần \(32 + 1 = 33\) túi hạt giống để gieo hết bãi cỏ.
Bài 5
Phương pháp:
Vận dụng phương pháp đánh giá từng vế của phương trình để tìm \(x,y,z\)
Cách giải:
Vì \({2^x},{3^y},{5^z} \ge 1,\forall x,y,z \in \mathbb{N}\)
\( \Rightarrow {5^z} < 156 < 625 = {5^4}\) \( \Rightarrow z < 4\)hay \(z \le 3\)
Với \(z = 2 \Rightarrow {2^x} + {3^y} + {5^2} = 156 \Rightarrow {2^x} + {3^y} = 131\)
Vì \(x \le y \le z \Rightarrow x \le y \le 2 \Rightarrow {2^x} + {3^y} \le {2^2} + {3^2} = 13\) (loại)
Vậy \(z = 3 \Rightarrow {2^x} + {3^y} + {5^3} = 156 \Rightarrow {2^x} + {3^y} = 156 - 125 = 31\)
Ta có: \(x \le y \le 3\)
Vì \({3^y} < 31 < 81 = {3^4} \Rightarrow y < 4\) hay \(y \le 3\)
Với \(y = 2 \Rightarrow {2^x} + {3^2} = 31 \Rightarrow {2^x} = 31 - 9 = 22\) (loại)
Với \(y = 1 \Rightarrow {2^x} + {3^1} = 31 \Rightarrow {2^x} = 31 - 3 = 28\) (loại)
Với \(y = 0 \Rightarrow {2^x} + {3^0} = 31 \Rightarrow {2^x} = 31 - 1 = 30\) (loại)
Với \(y = 3 \Rightarrow {2^x} + {3^3} = 31 \Rightarrow {2^x} = 31 - 27 = 4 = {2^2}\)\( \Rightarrow x = 2\)
Vậy \(x = 2;y = 3;z = 3\)