Trắc nghiệm 9.1
Vật A có khối lượng gấp hai lần vật B. Ném hai vật theo phương ngang với cùng tốc độ đầu ở cùng một vị trí. Nếu bỏ qua mọi lực cản thì
A. vị trí chạm đất của vật A xa hơn vị trí chạm đất của vật B.
B. vị trí chạm đất của vật B xa hơn vị trí chạm đất của vật A.
C. vật A và vật B rơi cùng vị trí.
D. chưa đủ dữ kiện để đưa ra kết luận về vị trí của hai vật.
Phương pháp giải:
Vận dụng kiến thức về tầm xa của chuyển động ném ngang.
Lời giải chi tiết:
Theo công thức tính tầm xa của vật ném ngang: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} \) trong đó v0 là vận tốc đầu của vật, h là độ cao của vị trí ném vật, g là gia tốc rơi tự do.
Do đó, nếu bỏ qua mọi lực cản thì tầm xa của hai vật ném ngang chỉ phụ thuộc vào tốc độ đầu và vị trí ném, mà hai yếu tố này của hai vật đều như nhau nên tầm xa của hai vật là như nhau.
=> Chọn C
Trắc nghiệm 9.2
Chọn từ/cụm từ thích hợp trong bảng dưới đây để điền vào chỗ trống.
|
rơi tự do |
parabol |
thẳng đứng |
ngang |
bằng nhau |
độ |
|
vận tốc |
khác nhau |
ném thẳng đứng |
thẳng đều |
đường thẳng |
nằm ngang |
- Đối với vật chuyển động ném ngang: Chuyển động của vật trên phương ngang là chuyển động (1) …, sau những khoảng thời gian bằng nhau vật đi được những đoạn đường (2) … Chuyển động của vật trên phương thẳng đứng là chuyển động (3) …, sau những khoảng thời gian bằng nhau vật đi được những đoạn đường (4) … Qũy đạo chuyển động của vật ném ngang là một nhánh của đường (5) ….
- Đối với chuyển động ném xiên: Chuyển động của vật trên phương ngang là (6) …, sau những khoảng thời gian bằng nhau vật đi được đoạn đường (7) … Chuyển động của vật trên phương thẳng đứng là chuyển động (8) …, sau những khoảng thời gian bằng nhau vật đi được những đoạn đường (9) … Qũy đạo chuyển động của vật ném xiên có dạng (10) … Vật đạt độ cao cực đại khi (11) … trên phương (12) … bằng không.
Phương pháp giải:
Vận dụng kiến thức về chuyển động ném ngang và chuyển động ném xiên.
Lời giải chi tiết:
- Đối với vật chuyển động ném ngang: Chuyển động của vật trên phương ngang là chuyển động (1) thẳng đều, sau những khoảng thời gian bằng nhau vật đi được những đoạn đường (2) bằng nhau. Chuyển động của vật trên phương thẳng đứng là chuyển động (3) rơi tự do, sau những khoảng thời gian bằng nhau vật đi được những đoạn đường (4) khác nhau. Qũy đạo chuyển động của vật ném ngang là một nhánh của đường (5) parabol.
- Đối với chuyển động ném xiên: Chuyển động của vật trên phương ngang là (6) thẳng đều, sau những khoảng thời gian bằng nhau vật đi được đoạn đường (7) bằng nhau. Chuyển động của vật trên phương thẳng đứng là chuyển động (8) ném thẳng đứng, sau những khoảng thời gian bằng nhau vật đi được những đoạn đường (9) khác nhau. Qũy đạo chuyển động của vật ném xiên có dạng (10) parabol. Vật đạt độ cao cực đại khi (11) vận tốc trên phương (12) thẳng đứng bằng không.
Trắc nghiệm 9.3
Trong tiết học Vật lí, ba bạn Mi, Hiếu và Đức tranh luận về thời gian rơi của vật chuyển động ném ngang so với vật thả rơi tự do khi ở cùng một độ cao và bỏ qua mọi lực cản. Bạn Mi cho rằng: “Khi ném một vật theo phương ngang thì vật sẽ chuyển động lâu hơn so với việc thả vật rơi tự do vì khi ném ngang, vật sẽ đi quãng đường dài hơn”. Bạn Hiếu lại có ý kiến khác: “Thời gian rơi của hai vật là bằng nhau vì trong cả hai trường hợp, tính chất chuyển động của vật theo phương thẳng đứng là như nhau”. Còn bạn Đức thì cho rằng: “Thời gian rơi khi vật chuyển động ném ngang còn phụ thuộc vào vận tốc ban đầu nên không thể kết luận về thời gian rơi trong hai trường hợp”. Theo em, bạn nào đã đưa ra ý kiến đúng?
A. Bạn Mi. B. Bạn Hiếu.
C. Bạn Hiếu. D. Cả ba bạn đều không chính xác.
Phương pháp giải:
Vận dụng kiến thức về đặc điểm của chuyển động ném ngang và chuyển động rơi tự do.
Lời giải chi tiết:
Thời gian rơi của vật ném ngang và rơi tự do là bằng nhau vì trong cả hai trường hợp, tính chất chuyển động của vật theo phương thẳng đứng là như nhau.
=> Chọn B
Trắc nghiệm 9.4
Một diễn viên đóng thế phải thực hiện một pha hành động khi điều khiển chiếc mô tô nhảy khỏi vách đá cao 50 m. Xe máy phải rời khỏi vách đá với tốc độ bao nhiêu để tiếp đất tại vị trí cách chân vách đá 90 m. Lấy g = 9,8 m/s2, bỏ qua lực cản không khí và xem chuyển động của mô tô khi rời vách đá là chuyển động ném ngang.
A. v0 = 11,7 m/s. B. v0 = 28,2 m/s.
C. v0 = 56,3 m/s. D. v0 = 23,3 m/s.
Phương pháp giải:
Công thức tính tầm xa của vật ném ngang: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} \) trong đó v0 là vận tốc đầu của vật, h là độ cao của vị trí ném vật, g là gia tốc rơi tự do nên suy ra: \({v_0} = L.\sqrt {\frac{g}{{2h}}} \).
Lời giải chi tiết:
Tóm tắt:
h = 50 m
L = 90 m
g = 9,8 m/s2
v0 =?
Lời giải:
Xe chuyển động như ném ngang, tầm xa của xe: \(L = {v_0}\sqrt {\frac{{2h}}{g}} \).
Xe máy phải rời khỏi vách đá với tốc độ: \({v_0} = L.\sqrt {\frac{g}{{2h}}} = 90.\sqrt {\frac{{9,8}}{{2.50}}} \approx 28,2\,m/s.\)
=> Chọn B
Trắc nghiệm 9.5
Một vận động viên sút một quả bóng bầu dục ba lần theo các quỹ đạo a, b và c như Hình 9.1. Qũy đạo nào tương ứng với thời gian chuyển động trong không khí của quả bóng là lâu nhất nếu bỏ qua mọi lực cản?
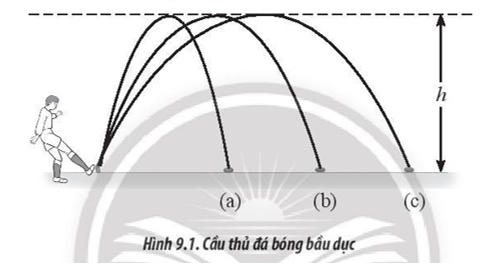
A. (a). B. (b).
C. (c). D. Cả ba trường hợp có thời gian chuyển động như nhau.
Phương pháp giải:
Thời gian rơi của vật trong chuyển động ném ngang từ độ cao h: \(t = \sqrt {\frac{{2h}}{g}} \)
Lời giải chi tiết:
Thời gian chuyển động của quả bóng trong cả 3 trường hợp là: \(t' = 2\sqrt {\frac{{2h}}{g}} \)
=> Chọn D
Tự luận 9.1
Khi phân tích chuyển động ném ngang của một vật trong trường hợp bỏ qua mọi lực cản, tính chất chuyển động của vật như nào theo phương thẳng đứng?
Phương pháp giải:
Vận dụng kiến thức về tính chất của chuyển động ném ngang.
Lời giải chi tiết:
Vật chuyển động thẳng nhanh dần đều theo phương thẳng đứng.
Tự luận 9.2
Trong chuyển động ném ngang, độ lớn vecto vận tốc của vật khi chạm đất lớn hơn, nhỏ hơn hay bằng với vecto vận tốc ban đầu? Tại sao?
Phương pháp giải:
Vận dụng kiến thức về tính chất của chuyển động ném ngang.
Lời giải chi tiết:
Độ lớn vecto vận tốc khi chạm đất: \(v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + v_y^2} > {v_0}.\)
Tự luận 9.3
Khi dùng với vòi nước tưới cây, để các tia nước phun ra xa, người ta thường điều chỉnh sao cho hướng của vòi xiên một góc nào đó với phương ngang (Hình 9.2). Trong trường hợp lí tưởng (bỏ qua mọi lực cản), góc hợp giữa vòi và phương ngang phải bằng bao nhiêu để các tia nước phun ra xa nhất?

Phương pháp giải:
Vận dụng công thức của tầm xa vật ném xiên:
\(L = {v_0}\cos \alpha \left( {{t_1} + {t_2}} \right) = \frac{{v_0^2\sin 2\alpha }}{{2g}} + {v_0}\cos \alpha \sqrt {\frac{{2\left( {H + h} \right)}}{g}} \)
Trong đó: v0 là vận tốc đầu, \(\alpha \) là góc hợp bởi vecto vận tốc và phương ngang ở thời điểm ban đầu, t1 là thời gian vật đạt độ cao cực đại \(\left( {{t_1} = \frac{{{v_0}\sin \alpha }}{g}} \right)\), t2 là thời gian vật từ độ cao cực đại tới đất \(\left( {{t_2} = \sqrt {\frac{{2\left( {H + h} \right)}}{g}} } \right)\) g là gia tốc trọng trường, h là độ cao của vật ở thời điểm ném vật, H là tầm cao của vật \(\left( {H = \frac{{v_0^2{{\sin }^2}\alpha }}{{2g}} + h} \right)\)
Lời giải chi tiết:
Trong bài toán của chúng ta, vòi nước coi như đặt tại mặt đất nên h = 0.
Viết lại biểu thức tầm xa của vật trong trường hợp này: \(L = \frac{{v_0^2\sin 2\alpha }}{g}\)
Khi đó tầm xa lớn nhất khi góc hợp giữa vòi và phương ngang phải bằng 450 (bỏ qua mọi lực cản).
Tự luận 9.4
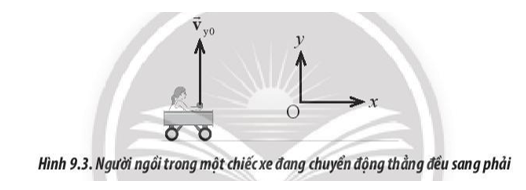
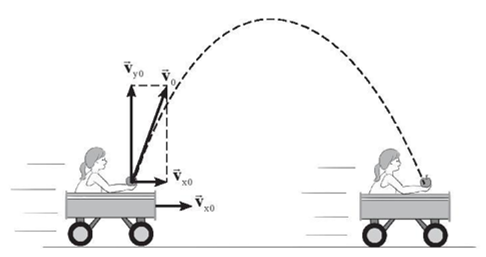
Một người ngồi trong chiếc xe đang chuyển động sang phải với tốc độ không đổi như Hình 9.3. Người này ném một quả táo thẳng đứng lên trên trong khi chiếc xe tiếp tục di chuyển với tốc độ không đổi. Nếu bỏ qua lực cản không khí, liệu quả táo sẽ rơi lại về tay người ném sau khi chuyển động lên không trung hay không, hay rơi về phía trước hoặc phía sau của xe? Giải thích tại sao?
Phương pháp giải:
Vận dụng kiến thức về hướng của vận tốc của vật trong chuyển động ném xiên.
Lời giải chi tiết:
Đối với người quan sát trên mặt đất, ngoài thành phần vận tốc theo phương thẳng đứng, quả táo còn chuyển động trên phương ngang cùng tốc độ với xe. Do đó quả táo chuyển động như vật bị ném xiên và rơi lại vào tay của người ném do người và quả táo có cùng vận tốc theo phương ngang.
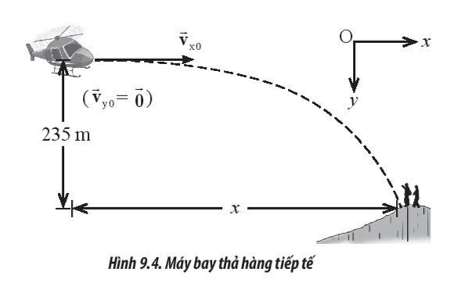
Tự luận 9.5
Một chiếc máy bay muốn thả hàng tiếp tế cho những người leo núi đang bị cô lập. Máy bay đang bay ở độ cao 235 m so với vị trí đứng của những người leo núi với tốc độ 250 km/h theo phương ngang (Hình 9.4). Máy bay phải thả hàng tiếp tế ở vị trí cách những người leo núi bao xa để họ có thể nhận hàng? Lấy g = 9,8 m/s2 và bỏ qua lực cản không khí.
Phương pháp giải:
Công thức tính tầm xa của vật ném ngang: \(L = {v_0}.\sqrt {\frac{{2h}}{g}} \) trong đó v0 là vận tốc đầu của vật, h là độ cao của vị trí ném vật, g là gia tốc rơi tự do.
Lời giải chi tiết:
Để người nhận được hàng tiếp tế, máy bay phải thả hàng ở vị trí người một khoảng:
\(L = {v_0}.\sqrt {\frac{{2h}}{g}} = \frac{{250}}{{3,6}}.\sqrt {\frac{{2.235}}{{9,8}}} \approx 480,9\,m.\)
