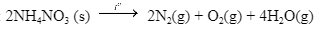Mở đầu
Phản ứng cháy, nổ được đặc trưng bởi hiệu ứng tỏa nhiệt mạnh, tốc độ phản ứng nhanh, phản ứng trước cung cấp nhiệt cho phản ứng sau và xảy ra nối tiếp. Vậy, hiệu ứng nhiệt của phản ứng đốt cháy một số nhiên liệu phổ biến được xác định như thế nào và giá trị thu được có ý nghĩa gì?
Lời giải chi tiết:
- Hiệu ứng nhiệt của phản ứng đốt cháy một số nhiên liệu phổ biến được xác định qua: nhiệt tạo thành, năng lượng liên kết
- Giá trị thu được cho biết phản ứng tỏa nhiệt mạnh không, tốc độ phản ứng nhanh không
CH mục I CH1
Xét phản ứng: CH4(g) + O2(g) → CO2(g) + 2H2O(g) \({\Delta _r}H_{298}^0 = - 802\) kJ
Tính \({\Delta _f}H_{298}^0\)CH4(g), biết \({\Delta _f}H_{298}^0\)của CO2 (g) và H2O (g) lần lượt là -394 kJ/mol và -242 kJ/mol.
Phương pháp giải:
\({\Delta _r}H_{298}^0 = \sum {H_{298}^0(sp) - } \sum {H_{298}^0(cd)} \)
Lời giải chi tiết:
Ta có:
\({\Delta _r}H_{298}^0(C{O_2})\)=-394 (kJ/mol)
\({\Delta _r}H_{298}^0({H_2}O) = - 242\)(kJ/mol)
\({\Delta _r}H_{298}^0({O_2}) = 0\) (kJ/mol)
Áp dụng công thức \({\Delta _r}H_{298}^0 = \sum {H_{298}^0(sp) - } \sum {H_{298}^0(cd)} \)
=> \( - 802 = 1.( - 394) + 2.( - 242) - {\Delta _f}H_{298}^0(C{H_4})\)
\(\)=> \({\Delta _f}H_{298}^0(C{H_4}) = - 76\) (kJ/mol)
CH mục I CH2
Tính nhiệt lượng tỏa ra khi đốt cháy 1 kg một loại củi khô, biết củi khô chứa 54% khối lượng cellulose và phân tử cellulose được cấu tạo bơi các gốc glucose
Giả thiết toàn bộ nhiệt lượng tỏa ra được tính từ biến thiên enthalpy của phản ứng đốt cháy glucose:
C6H10O5(s) + 5O2(g) → 6CO2(g) + 5H2O(l) \({\Delta _r}H_{298}^0\)= -2 880 kJ
Phương pháp giải:
Đốt cháy 1 mol glucose sẽ tỏa ra nhiệt lượng là 2 880 kJ
=> Đốt cháy 162 gam glucose sẽ tỏa ra nhiệt lượng là 2 880 kJ
Trong x gam củi sẽ có 162 gam glucose, tỏa ra nhiệt lượng là 2 880 kJ
x = 162 : 54%
=> 1000 gam củi sẽ tỏa ra: 2 880 . 1000 : x
Lời giải chi tiết:
Đổi 1kg = 1000 gam
Đốt cháy 1 mol glucose sẽ tỏa ra nhiệt lượng là 2 880 kJ.
⇒ Đốt cháy 0,162 kg glucose sẽ tỏa ra nhiệt lượng là 2 880 kJ.
Trong x gam củi sẽ có 162 gam glucose, tỏa ra nhiệt lượng là 2 880 kJ
x = 162 : 54% = 300 gam (vì củi khô chứ 54% khối lượng cellulose và phân tử cellulose được cấu tạo bởi các gốc glucose
=> Đốt cháy 300 gam củi khô sẽ tỏa ra nhiệt lượng là 2 880 kJ
Vậy đốt cháy 1000 gam củi khô sẽ tỏa nhiệt lượng là 2 880 . 1000 : 300 = 9600 kJ
CH mục I CH3
Ngày 04 tháng 8 năm 2020 đã xảy ra một vụ nổ kinh hoàng ở nhà kho tại cảng Beriut của Lebanon. Đây là nhà kho chứa khoảng 2700 tấn NH4NO3, một loại hóa chất vừa được sử dụng làm phân bón, vừa được dùng làm thuốc nổ do có khả năng phân hủy thành khí và hơi, kèm theo tỏa nhiệt mạnh:
Phương pháp giải:
a) Tính \({\Delta _r}H_{298}^0\) của phản ứng, biết \({\Delta _f}H_{298}^0\) của NH4NO3 (s) và \({\Delta _f}H_{298}^0\)của H2O(g) lần lượt là -365,6 kJ/mol và -242 kJ/mol.
b) Tính nhiệt lượng tối đa giải phóng ra từ vụ nổ khi toàn bộ lượng NH4NO3 bị phân hủy
Lời giải chi tiết:
a)
Vì nhiệt hình thành của đơn chất = 0 nên:
\(\begin{array}{l}{\Delta _f}H_{298}^0({H_2}O) = - 242(kJ/mol)\\{\Delta _f}H_{298}^0({O_2}) = 0(kJ/mol)\\{\Delta _f}H_{298}^0({N_2}) = 0(kJ/mol)\\{\Delta _f}H_{298}^0(N{H_4}N{O_3}) = - 365,6(kJ/mol)\end{array}\)
Áp dụng công thức: \({\Delta _r}H_{298}^0 = \sum {H_{298}^0(sp) - } \sum {H_{298}^0(cd)} \)
\(\begin{array}{l} = 2.0 + 1.0 + 4( - 242) - 2.( - 365,6)\\ = - 236,8(kJ)\end{array}\)
b)
Ta có: 2700 tấn NH4NO3 tương ứng với 3375.104 mol NH4NO3.
Nhiệt lượng tỏa ra khi nổ 1 mol NH4NO3 là 236,8 kJ.
⇒ Nhiệt lượng tỏa ra khi nổ 3375.104 mol NH4NO3 là 236,8.3375.104 = 79,92.108 kJ.
CH mục II CH4
Một người ngủ quên trong ô tô tắt máy, đóng kín cửa. Sau một thời gian, khi phần trăm thể tích oxygen giảm xuống còn 16% thì rất may có người kịp thời phát hiện, phá vỡ kính xe để đưa đi cấp cứu.
Hỏi tại thời điểm có người đến cứu, tốc độ “phản ứng hô hấp” của người trong xe giảm bao nhiêu lần so với bình thường? Giả thiết vhô hấp = k.CO2
Phương pháp giải:
- Với phần trăm thể tích oxygen ban đầu (21%) thì v(21% O2) = k.CO2 = k.0,21
- Với phần trăm thể tích oxygen giảm cần 16% thì v(16% O2) = k.CO2 = k.0,16
Tính tỉ lệ
Lời giải chi tiết:
- Với phần trăm thể tích oxygen ban đầu (21%) thì v(21% O2) = k.CO2 = k.0,21
- Với phần trăm thể tích oxygen giảm cần 16% thì v(16% O2) = k.CO2 = k.0,16
Tốc độ “phản ứng hô hấp” giảm so với điều kiện bình thường là:
\(\frac{{{V_{(21\% {O_2})}}}}{{{V_{(16\% {O_2})}}}} = \frac{{k.0,21}}{{k.0,16}} = 1,3125\)(lần)
CH mục II CH5
Đỉnh Fansipan (có độ cao 3 147 m so với mực nước biển) là ngọn núi cao nhất Việt Nam. Giả thiết không khí trên đỉnh Fansipan có áp suất 0,66 atm và chứa 21% thể tích oxygen. Hỏi tốc độ “phản ứng hô hấp” giảm bao nhiêu lần so với điều kiện bình thường? Giả thiết vhô hấp = k.CO2
Phương pháp giải:
- Ở điều kiện bình thường, áp suất là 1 atm thì áp suất riêng phần của O2 là 1.21% = 0,21 atm
- Ở trên đỉnh Fansipan, áp suất là 0,66 atm thì áp suất riêng phần của O2 là 0,66.21% = 0,14 atm
Lời giải chi tiết:
- Ở điều kiện bình thường, áp suất là 1 atm thì áp suất riêng phần của O2 là 1.21% = 0,21 atm
- Ở trên đỉnh Fansipan, áp suất là 0,66 atm thì áp suất riêng phần của O2 là 0,66.21% = 0,14 atm
Do nồng độ oxygen tỉ lệ thuận với áp suất nên tỉ lệ tốc độ “phản ứng hô hấp” giữa 2 áp suất là
\(\frac{{{V_{({P_{{O_2}}} = 0,14atm)}}}}{{{V_{({P_{{O_2}}} = 0,21atm)}}}} = \frac{{k{C_{({P_{{O_2}}} = 0,14atm)}}}}{{k{C_{({P_{{O_2}}} = 0,21atm)}}}} = \frac{{k.{P_{_{({P_{{O_2}}} = 0,14atm)}}}}}{{k.{P_{_{({P_{{O_2}}} = 0,21atm)}}}}} = \frac{{0,14}}{{0,21}} = \frac{2}{3}\) (lần)
=> Tốc độ “phản ứng hô hấp” giảm 1,5 lần