Bài 1
Video hướng dẫn giải
Bạn Dung tính nhẩm 15% của 120 như sau:
10% của 120 là 12
5% của 120 là 6
Vậy : 15% của 120 là 18.
a) Hãy viết số thích hợp vào chỗ chấm để tìm 17,5% của 240 theo cách tính của bạn Dung:
... % của 240 là ...
... % của 240 là ...
... % của 240 là ...
Vậy : 17,5% của 240 là ...
b) Hãy tính 35% của 520 và nêu cách tính.
Phương pháp giải:
*) - Phân tích 15% = 10% + 5%
- Tính nhẩm 10% của 120 bằng cách lấy 120 chia nhẩm 10.
- Tính nhẩm 5% bằng cách lấy giá trị 10% của 120 chia cho 2.
- 15% của 120 = 10% của 120 + 5% của 120.
*) Ta tính tương tự như trên để tìm 17,5% của 240.
Lời giải chi tiết:
a) 10% của 240 là 24.
5% của 240 là 12.
2,5% của 240 là 6.
Vậy : 17,5% của 240 là 42.
b) Cách 1 :
10% của 520 là 52. Vậy:
30% của 520 là 156.
5% của 520 là 26.
Vậy : 35% của 520 là 182.
Cách 2 :
10% của 520 là 52.
5% của 520 là 26.
20% của 520 là 104.
Vậy : 35% của 520 là 182.
Cách 3:
10% của 520 là 52.
70 % của 520 là 364.
Vậy : 35 % của 520 là 182.
Bài 2
Video hướng dẫn giải
Biết tỉ số thể tích của hai hình lập phương là 2 : 3 (xem hình vẽ).
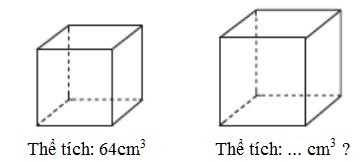
a) Thể tích của hình lập phương lớn bằng bao nhiêu phần trăm thể tích của hình lập phương bé ?
b) Tính thể tích của hình lập phương lớn.
Phương pháp giải:
- Tìm tỉ số thể tích của hình lập phương lớn và hình lập phương bé rồi viết dưới dạng tỉ số phần trăm.
- Muốn tìm thể tích hình lập phương lớn ta lấy thể tích hình lập phương bé nhân với tỉ số thể tích của hình lập phương lớn và hình lập phương bé.
Lời giải chi tiết:
a) Vậy tỉ số phần trăm thể tích hình lập phương lớn và thể tích hình lập phương bé là:
\(3 : 2 = 1,5 = 150\%\)
b) Thể tích hình lập phương lớn là:
\(64 \times\dfrac{3}{2} = 96\; (cm^3)\)
Đáp số: a) \(150\%\);
b) \(96cm^3\).
Bài 3
Video hướng dẫn giải
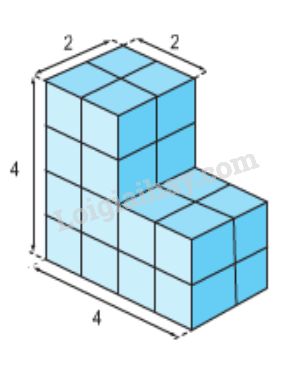
Bạn Hạnh xếp các hình lập phương nhỏ có cạnh 1cm thành hình bên. Hỏi:
a) Hình bên có bao nhiêu hình lập phương nhỏ ?
b) Nếu sơn các mặt ngoài của hình bên thì diện tích cần sơn bằng bao nhiêu xăng-ti-mét vuông ?
Phương pháp giải:
Quan sát hình vẽ để tìm số hình lập phương nhỏ có trong hình đã cho.
- Áp dụng công thức tính diện tích một mặt: Diện tích một mặt = cạnh \(\times \) cạnh.
Lời giải chi tiết:
a) Coi hình đã cho gồm 3 khối lập phương lớn, mỗi khối đều được xếp bởi 8 hình lập phương nhỏ, như vậy hình vẽ có tất cả:
8 × 3 = 24 (hình lập phương nhỏ)
b) Cách 1:
Ta có hình vẽ :
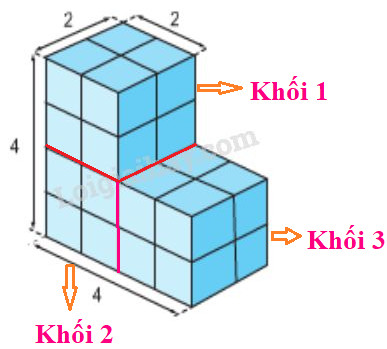
Số mặt của hình lập phương cạnh 2cm là:
6 × 3 = 18 (mặt)
Khối 1 có 1 mặt không được sơn (mặt bên dưới của khối 1).
Khối 2 có 2 mặt không được sơn (mặt bên trên và mặt bên phải của khối 2).
Khối 3 có 1 mặt không được sơn (mặt bên trái của khối 3).
Như vậy có 4 mặt không phải sơn, do đó số mặt được sơn là 18 - 4 = 14 (mặt)
Diện tích một mặt của hình lập phương lớn là:
2 × 2 = 4 (cm2)
Vậy diện tích cần sơn của hình đã cho là:
4 × 14 = 56 (cm2)
Cách 2:
Mỗi khối lập phương cạnh 2cm nêu ở phần a) có diện tích toàn phần là:
(2 × 2) × 6 = 24 (cm2)
Diện tích toàn phần của 3 khối là:
24 × 3 = 72 (cm2)
Ta có hình vẽ :
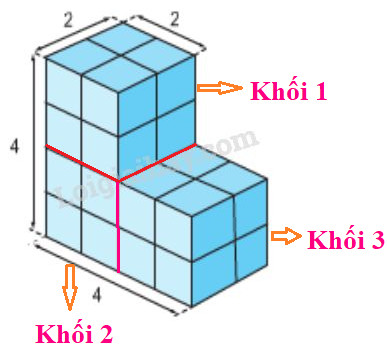
Khối 1 có 1 mặt không được sơn (mặt bên dưới của khối 1).
Khối 2 có 2 mặt không được sơn (mặt bên trên và mặt bên phải của khối 2).
Khối 3 có 1 mặt không được sơn (mặt bên trái của khối 3).
Cả 3 khối có số mặt không được sơn là:
1 + 2 + 1 = 4 (mặt)
Diện tích phần không sơn của hình đã cho là:
(2 × 2) × 4 = 16 (cm2)
Diện tích cần sơn của hình đã cho là:
72 – 16 = 56 (cm2)
Đáp số: a) 24 hình;
b) 56cm2.
