Đề bài
Chứng minh rằng phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đó.
Lời giải chi tiết
Giả sử phép tịnh tiến \({T_{\overrightarrow u }}\) biến đường thẳng d thành đường thẳng d’.
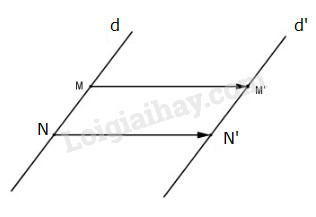
Lấy hai điểm phân biệt M, N trên d và gọi M’, N’ lần lượt là ảnh của M, N qua phép tịnh tiến \({T_{\overrightarrow u }}\) thì M’, N’ nằm trên d’.
Ta có \(\overrightarrow {MN} = \overrightarrow {M'N'} \). Vậy hai đường thẳng d và d’ có cùng vecto chỉ phương nên d//d’ hoặc trùng với d’.
d trùng với d’ khi \(\overrightarrow u \) cùng phương với \(\overrightarrow {MN} \), tức là khi \(\overrightarrow u \) là vecto chỉ phương của d hoặc \(\overrightarrow u = \overrightarrow v \) ;
d//d' khi \(\overrightarrow u \) không phải là vecto chỉ phương của d.
soanvan.me
