Đề bài
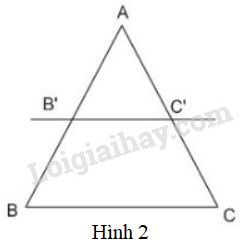
Cho biết \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\) (h.6)
Chứng minh rằng:
a) \(\dfrac{AB'}{B'B}= \dfrac{AC'}{C'C}\)
b) \(\dfrac{BB'}{AB} = \dfrac{CC'}{AC}\).
Phương pháp giải - Xem chi tiết
- Áp dụng định lí TaLet và tính chất dãy tỉ số bằng nhau.
Lời giải chi tiết
a) Theo giả thiết ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
Theo tính chất của tỉ lệ thức (trừ các mẫu cho tử tương ứng và giữ nguyên tử) ta có:
\(\dfrac{{AB'}}{{AB - AB'}} = \dfrac{{AC'}}{{AC - AC'}}\) hay \( \dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\) (đpcm).
b) Theo giả thiết ta có: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
Theo tính chất của tỉ lệ thức (trừ các mẫu cho tử tương ứng và giữ nguyên mẫu) ta có:
\(\dfrac{{AB - AB'}}{{AB}} = \dfrac{{AC - AC'}}{{AC}}\) hay \( \dfrac{BB'}{AB}= \dfrac{CC'}{AC}\) (đpcm).
soanvan.me
