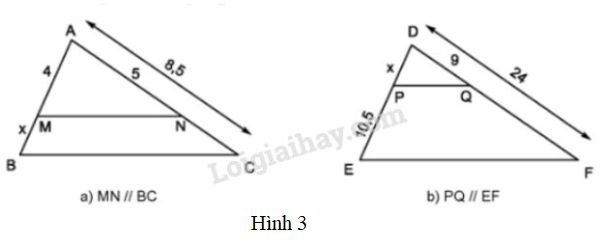
Tìm \(x\) trong các trường hợp sau (h.7):
LG a
Phương pháp giải:
Áp dụng định lý Ta-let trong tam giác.
Lời giải chi tiết:
\(MN // BC\) (h.3a); theo định lí Ta-lét ta có:
\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}}\) hay \(\dfrac{4}{{4 + x}} = \dfrac{5}{{8,5}}\)
\(\begin{array}{l}
\left( {4 + x} \right).5 = 4.8,5\\
4 + x = \dfrac{{4.8,5}}{5}\\
x = \dfrac{{4.8,5}}{5} - 4
\end{array}\)
Tính trên máy tính bỏ túi, ta được \(x = 2,8\).
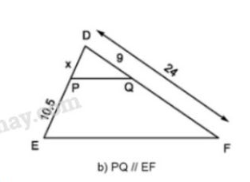
LG b
Phương pháp giải:
Áp dụng định lý Ta-let trong tam giác.
Lời giải chi tiết:
\(PQ // EF\) (h.3b); theo định lí Ta-lét ta có:
\( \dfrac{DP}{PE} = \dfrac{DQ}{QF}\) hay \(\dfrac{x}{10,5} = \dfrac{9}{24-9}\)
\( x = \dfrac{10,5.9}{24-9} \)
Tính trên máy tính bỏ túi, ta được \(x=6,3\).
soanvan.me
