Đề bài
Trong mặt phẳng (\( \alpha\)) cho hình bình hành \(ABCD\). Qua \(A, B, C, D\) lần lượt vẽ bốn đường thẳng \(a,b,c,d\) song song với nhau và không nằm trên (\( \alpha\)). Trên \(a, b, c\) lần lượt lấy ba điểm \(A', B', C'\) tùy ý
a) Hãy xác định giao điểm \(D'\) của đường thẳng \(d\) với mặt phẳng \((A'B'C')\).
b) Chứng minh \(A'B'C'D'\) là hình bình hành.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Xác định điểm chung của \(d\) và \((A'B'C')\).
b) Sử dụng nội dung của định lí 3: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết
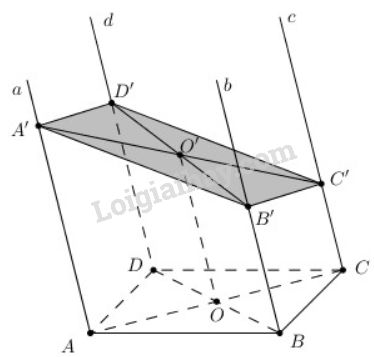
a) Gọi \(O = AC ∩ BD\); \(O'\) là trung điểm \(A'C'\) thì OO' là đường trung bình của hình thang \(ACC'A'\) \(\Rightarrow OO' // AA'\)
\(\Rightarrow OO'// d // b\) mà \(OO' \subset mp (b;d) \Rightarrow O' \in mp (b;d) \) ( mặt phẳng xác định bởi hai đường thẳng song song).
Trong \(mp (b;d)\), gọi \(D'=d ∩ B'O'\) ta có:
\(\left\{ \begin{array}{l}D' \in B'O' \subset \left( {A'B'C'} \right)\\D' \in d\end{array} \right. \)
\(\Rightarrow D' = d \cap \left( {A'B'C'} \right)\) chính là điểm cần tìm.
b) \(mp(a;d) // mp( b;c)\) , mặt phẳng thứ 3 \((A'B'C'D')\) cắt hai mặt phẳng trên theo hai giao tuyến song song : \(A'D' // B'C'\). Chứng minh tương tự được \(A'B' // D'C'\).
Từ đó suy ra \(A'B'C'D'\) là hình bình hành.
Cách khác:
a) Giả sử \(\left( {ABC} \right) \cap {\rm{ }}d = {\rm{ }}D\)
\(\begin{array}{*{20}{l}}
{ \Rightarrow \left( {ABC} \right) \cap \left( {CCD} \right) = {\rm{ }}CD.}\\
{ + {\rm{ }}AA//CC \subset \left( {CCD} \right)}\\
{ \Rightarrow {\rm{ }}AA//\left( {CCD} \right).}\\
{AB//CD \subset \left( {CCD} \right)}\\
{ \Rightarrow {\rm{ }}AB//\left( {CCD} \right)}
\end{array}\)
\((AA’B’B)\) có: \(\left\{ \begin{array}{l}AA'//\left( {C'CD} \right)\\AB//\left( {C'CD} \right)\\AA' \cap AB\end{array} \right.\)
\( \Rightarrow {\rm{ }}\left( {AABB} \right){\rm{ }}//{\rm{ }}\left( {CCD} \right).\)
Mà \(\left( {ABC} \right) \cap \left( {AABB} \right) = {\rm{ }}AB\)
\(⇒ (A’B’C’)\) cắt \((C’CD)\) và giao tuyến song song với \(A’B’\)
\(⇒ C’D’ // A’B’.\)
b) Chứng minh tương tự phần \(a\) ta có \(B’C’ // A’D’.\)
Tứ giác \(A’B’C’D’\) có: \(B’C’ // A’D’\) và \(C’D’ // A’B’\)
\(⇒ A’B’C’D’\) là hình bình hành.
soanvan.me
