Đề bài
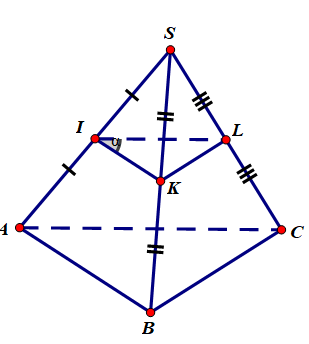
Cho tứ diện \(SABC\). Hãy dựng mặt phẳng \((α)\) qua trung điểm \(I\) của đoạn \(SA\) và song song với mặt phẳng \((ABC)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cách 1: Xác định mp \((\alpha)\):
Gọi các giao điểm của \((\alpha)\) với các cạnh \(SB, SC.\) Chỉ ra đặc điểm và xác định vị trí của các giao điểm ấy.
Cách 2: Lấy K, L là trung điểm của SB, SC. Chứng minh: \(\left( \alpha \right) \equiv \left( {IKL} \right)\)
Lời giải chi tiết
Cách 1:
Gọi \(K, L\) lần lượt là giao của mp \((\alpha)\) với các cạnh \(SB, SC.\)
Ta có: \((\alpha) \, // \, (ABC)\)
\(\begin{array}{l}
\Rightarrow \left\{ \begin{array}{l}
IK\;//\;\left( {ABC} \right) \supset AB\\
IL\;//\;\left( {ABC} \right) \supset AC
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
IK\;//\;AB\\
IL\;//\;AC
\end{array} \right.
\end{array}\)
Mà \(I\) là trung điểm của \(SA.\)
\( \Rightarrow \left\{ \begin{array}{l}
K\text {là trung điểm cạnh SB}\\
I\;\text {là trung điểm cạnh SC}
\end{array} \right.\)
Vậy mp \((\alpha)\) chính là mp \((IKL).\)
Cách 2:
Mặt phẳng \((α)\) là mặt phẳng đi qua 3 trung điểm \(I, K, L\) của \(SA, SB, SC\)
Thật vậy, gọi \( K , L\) lần lượt là trung điểm của \(SB, SC\)
Suy ra \(IK, KL\) lần lượt là đường trung bình trong tam giác \(SAB\) và \(SBC\)
\(IK//{\rm{ }}AB \in \left( {ABC} \right) \Rightarrow {\rm{ }}IK//\left( {ABC} \right)\)
\(KL//{\rm{ }}BC \in \left( {ABC} \right) \Rightarrow {\rm{ }}KL//\left( {ABC} \right)\)
\(IK\) và \(KL\) cắt nhau và cùng song song với mp \((ABC)\)
⇒ Mặt phẳng chứa \(IK\) và \(KL\) song song với mp \((ABC)\)
Hay \((α) // (ABC)\).
soanvan.me