Đề bài
Cho góc bẹt xOy. Trên cùng nửa mặt phẳng bờ xy, vẽ hai ta Om và On sao cho \(\widehat {xOm} = {42^o},\widehat {yOn} = {75^o}\).
a) Tính \(\widehat {xOn}\).
b) Gọi Ot là tia phân giác của góc xOm. Tính \(\widehat {tOn}\).
Lời giải chi tiết
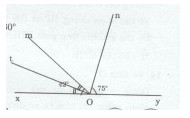
a)Góc xOy là góc bẹt nên \(\widehat {xOy} = {180^0}.\)
Hai góc \(\widehat {xOn}\) và \(\widehat {yOn}\) kề bù nên \(\widehat {xOn} + \widehat {yOn} = {180^0}.\)
\( \Rightarrow \widehat {xOn} = {180^0} - {75^0} = {105^0}.\)
b) Ot là tia phân giác của góc xOm
Nên \(\widehat {xOt} = \widehat {mOt} = {{\widehat {xOm}} \over 2} = {{{{42}^0}} \over 2} = {21^0}.\)
Hai tia Ot và On cùng thuộc một nửa mặt phẳng chứa tia Ox, \(\widehat {xOt} < \widehat {xOn}({21^0} < {105^0})\) nên tia Ot nằm giữa hai tia Ox và On.
Ta có: \(\widehat {xOt} + \widehat {tOn} = \widehat {xOn} \)
\(\Rightarrow \widehat {tOn} = \widehat {xOn} - \widehat {xOt} = {105^0} - {21^0} = {84^0}.\)
soanvan.me
