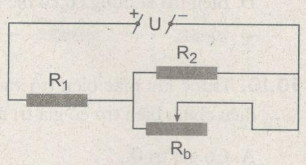
Đề bài

Một biến trở Rb có giá trị lớn nhất là 30Ω được mắc với hai điện trở R1=15Ω và R2=10Ω thành mạch có sơ đồ như hình 10.5 , trong đó hiệu điện thế không đổi U=4,5V. Hỏi khi điều chỉnh biến trở thì cường độ dòng điện chạy qua điện trở R1 có giá trị lớn nhất Imax và nhỏ nhất Imin là bao nhiêu?
 

Phương pháp giải - Xem chi tiết

+ Sử dụng biểu thức tính điện trở tương đương của đoạn mạch gồm các điện trở mắc song song: \({R_{tđ}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} \)

+ Sử dụng biểu thức định luật ôm: \({I} = \dfrac{U}{R}\)

+ Sử dụng biểu thức  tính điện trở tương đương của đoạn mạch gồm các điện trở mắc nối tiếp: \({R_{tđ}} = R_1+R_2\)

Lời giải chi tiết

Mạch gồm: \(R_1\) Nt [ \(R_2\) // \(R_{b}\)]
Điện trở \(R_2\) và \(R_b\):

\(\dfrac{1}{R_{2b}} = \dfrac{1}{R_2} + \dfrac{1}{R_b}= \dfrac{1}{10} + \dfrac{1}{30} \Rightarrow {R_{2b}} = 7,5\Omega \)

Điện trở tương đương toàn mạch:

\(R_{tđ}= R_1+ R_{2b}\)= \(15+ 7,5 =22,5 \Omega\)

Cường độ dòng điện nhỏ nhất :

\({I_{\min }} = \dfrac{U}{R_{tđ}}= \dfrac{4,5}{22,5} = 0,2{\rm{A}}\)

Cường độ dòng điện lớn nhất :\(I_{max}  → R_b\)  rất nhỏ \((R_b= 0)\)

 \({I_{\max }} = {I_1} = \dfrac{U}{R_1} = \dfrac{4,5}{15} = 0,3A\) 

soanvan.me