Đề bài
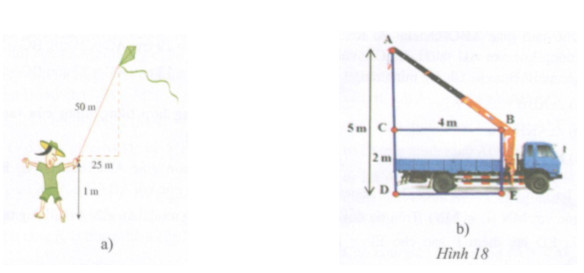
a) Tính độ cao của con diều so với mặt đất (h.18a).
b) Tính chiều dài cần cẩu AB (h.18b).
Lời giải chi tiết
a)Gọi độ cao của con diều so với tay người thả là h (m).
Áp dụng định lý Pythagore trong tam giác vuông ta có: \({h^2} + {25^2} = {50^2}.\)
\(\Rightarrow {h^2} = {50^2} - {25^2} = 2500 - 625 = 1875\)
Mà h > 0 do đó \(h = \sqrt {1875} \approx 43,3 (m)\)
Độ cao của con diều so với mặt đất là: \(43,3 + 1 = 44,3 (m).\)
b) \(AC = AD - CD = 5 - 2 = 3(m)\)
Áp dụng định lý Pythagore cho tam giác ABC vuông tại C ta có: \(A{B^2} = A{C^2} + B{C^2}\)
Do đó: \(A{B^2} = {3^2} + {4^2} = 9 + 16 = 25\)
Mà AB > 0 nên \(AB = \sqrt {25} = 5(m).\) Vậy chiều dài của cần cẩu là 5m.
