Đề bài
Hai bóng đèn có cùng hiệu điện thế định mức là U1=6V, khi sáng bình thường có điện trở tương ứng là R1=8Ω và R2=12Ω. Cần mắc hai bóng đèn này với một biến trở vào hiệu điện thế U=9V để hai đèn sáng bình thường.
a. Vẽ sơ đồ của mạch điện trên và tính điện trở của biến trở khi đó.
b. Biến trở được quấn bằng dây hợp kim nikêlin có điện trở suất 0,40.10-6Ω.m, tiết diện tròn, chiều dài 2m. Tính đường kính tiết diện d của dây hợp kim này, biết rằng hiệu điện thế lớn nhất được phép đặt vào hai đầu của biến trở là 30V và khi đó dòng điện chạy qua biến trở có cường độ là 2A.
Phương pháp giải - Xem chi tiết
+ Sử dụng biểu thức định luật ôm: \({I} =\dfrac{U}{R}\)
+ Sử dụng biểu thức tính điện trở của dây dẫn: \(R=\dfrac{\rho.l}{S}\)
Lời giải chi tiết
a. Sơ đồ mạch điện như hình dưới đây:
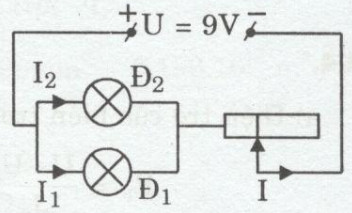
Mạch gồm : [\(Đ_1\) // \(Đ_2\)] Nt \(R_b\). Vì hai đèn sáng bình thường nên ta có:
- Cường độ dòng điện qua đèn 1 là:
\({I_1} =\dfrac{U_1}{R_1} = \dfrac{6}{8} = 0,75{\rm{A}}\)
- Cường độ dòng điện qua đèn 2 là:
\({I_2} = \dfrac{U_2}{R_2} = \dfrac{6}{12} = 0,5{\rm{A}}\)
Cường độ dòng điện qua mạch chính là:\( I = I_1 + I_2 = 1,25A\)
-Điện trở của biến trở là : \({R_b} = \dfrac{U_b}{I}=\dfrac{U - {U_1}}{ I} = \dfrac{9 - 6}{1,25} = 2,4\Omega\)
b) Điện trở lớn nhất của biến trở là: \({R_{\max }} = \dfrac{U_{\max }}{I_{\max }}= \dfrac{30}{2} = 15\Omega\)
Tiết diện của dây là:
\(S = \dfrac{\rho l}{R} = \dfrac{0,4.{10}^{ - 6}.2}{15} = 0,053.{10^{ - 6}}{m^2} = 0,053m{m^2}\)
Vì dây dẫn có tiết diện tròn nên \(S = \dfrac{\pi.d^2}{4}\)
\(\Rightarrow d = 2\sqrt {\dfrac{S}{\pi }} = 2\sqrt {\dfrac{0,053}{3,14}} = 0,26mm\)
soanvan.me
