Tìm cực trị của các hàm số sau:
LG a
\(f(x) = {{{x^2} + 8x - 24} \over {{x^2} - 4}}\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 2;2} \right\}\)
\(\begin{array}{l}f'\left( x \right) = \frac{{\left( {2x + 8} \right)\left( {{x^2} - 4} \right) - \left( {{x^2} + 8x - 24} \right).2x}}{{{{\left( {{x^2} - 4} \right)}^2}}}\\ = \frac{{2{x^3} + 8{x^2} - 8x - 32 - 2{x^3} - 16{x^2} + 48x}}{{{{\left( {{x^2} - 4} \right)}^2}}}\\ = \frac{{ - 8{x^2} + 40x - 32}}{{{{\left( {{x^2} - 4} \right)}^2}}}\\f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\end{array}\)
BBT:
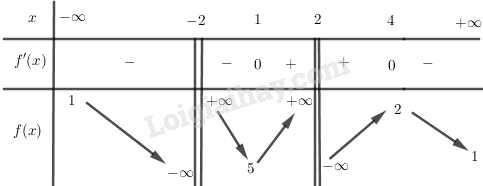
Hàm số đạt cực tiểu tại điểm x = 1; f(1) = 5 và đạt cực đại tại điểm x = 4; f(4) = 2
LG b
\(f(x) = {x \over {{x^2} + 4}}\)
Lời giải chi tiết:
TXĐ: \(D = \mathbb{R}\)
\(\begin{array}{l}f'\left( x \right) = \frac{{{x^2} + 4 - 2{x^2}}}{{{{\left( {{x^2} + 4} \right)}^2}}} = \frac{{4 - {x^2}}}{{{{\left( {{x^2} + 4} \right)}^2}}}\\f'\left( x \right) = 0 \Leftrightarrow 4 - {x^2} = 0 \Leftrightarrow x = \pm 2\end{array}\)
BBT:
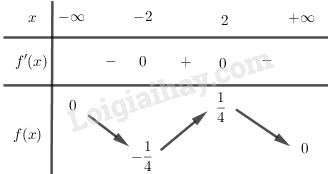
Hàm số đạt cực đại tại điểm \(x = - 2;{\rm{ }}f\left( { - 2} \right) = - {1 \over 4}\) và đạt cực tiểu tại điểm \(x = 2;{\rm{ }}f\left( 2 \right) = {1 \over 4}\)
LG c
\(f(x) = x\sqrt {3 - x} \)
Lời giải chi tiết:
TXĐ: \(D = \left( { - \infty ;3} \right]\)
\(\begin{array}{l}f'\left( x \right) = \sqrt {3 - x} + \frac{{ - x}}{{2\sqrt {3 - x} }}\\ = \frac{{2\left( {3 - x} \right) - x}}{{2\sqrt {3 - x} }} = \frac{{6 - 3x}}{{2\sqrt {3 - x} }}\\f'\left( x \right) = 0 \Leftrightarrow 6 - 3x = 0\\ \Leftrightarrow x = 2\end{array}\)
BBT:
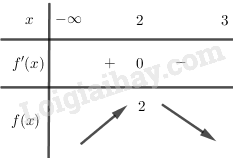
Hàm số đạt cực đại tại điểm x = 2; f(2) = 2.
LG d
\(f(x) = {x^2} - 2\left| x \right| + 2\)
Lời giải chi tiết:
Hàm số liên tục trên R
\(f(x) = \left\{ \matrix{{x^2} + 2x + 2;x < 0 \hfill \cr {x^2} - 2x + 2;x \ge 0 \hfill \cr} \right.\)
\(f'(x) = \left\{ \matrix{2x + 2;x < 0 \hfill \cr 2x - 2;x > 0 \hfill \cr} \right.\)
\(f'(x) = 0 \Leftrightarrow x = - 1,x = 1\)
Bảng biến thiên
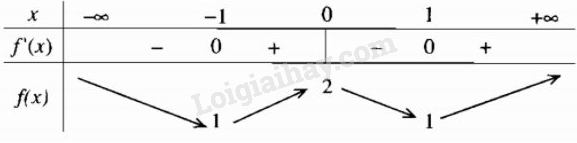
Hàm số đạt cực đại tại điểm \(x = 0,f(0) = 2\) và đạt cực tiểu tại các điểm x = -1 và x = 1; \(f( - 1) = f(1) = 1\)
soanvan.me
