Đề bài
Một hình trụ có bán kính đường tròn đáy \(3cm\), chiều cao \(4cm\) được đặt đứng trên mặt bàn. Một phần của hình trụ bị cắt rời ra theo các bán kính \(OA,\) \(OB\) và theo chiều thẳng đứng từ trên xuống dưới với (xem hình 92).
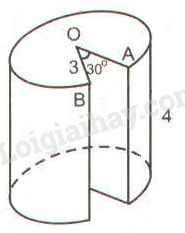
Hãy tính:
a) Thể tích phần còn lại.
b) Diện tích toàn bộ của hình sau khi đã bị cắt.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Công thức tính diện tích xung quanh hình trụ: \({S_{xq}} = 2πrh\).
- Công thức tính thể tích hình trụ: \(V= Sh = πr^2h\).
(\(r\) là bán kính đường tròn đáy, \(h\) là chiều cao, \(S\) là diện tích đáy).
Lời giải chi tiết
a) Thể tích hình trụ là:
\(\begin{array}{l}
V = \pi {r^2}.h\\
V = \pi {.3^2}.4 = 36\pi (c{m^3})
\end{array}\)
Phần hình trụ bị cắt đi bằng \(\displaystyle {{30^\circ } \over {360^\circ }}={1 \over {12}}\) (hình trụ)
Phần hình trụ còn lại bằng \(\displaystyle 1 - {1 \over {12}} = {{11} \over {12}}\) (hình trụ)
Thể tích phần hình trụ còn lại là: \(\displaystyle {{11} \over {12}}.36\pi = 33\pi (c{m^3})\)
b) Phần diện tích xung quanh còn lại (không kể phần lõm): \(S = 2. π. 3. 4. \displaystyle{{11} \over {12}} = 22π\; (c{m^2})\)
Phần diện tích còn lại của \(2\) đáy là: \(\displaystyle \pi {.3^2}.{{11} \over {12}}.2 = {{33\pi } \over 2}(c{m^2})\)
Diện tích phần lõm là hai hình chữ nhật kích thước \(3\) và \(4\) là:
\(2.(3.4)=24\;(cm^2)\)
Diện tích toàn bộ hình sau khi cắt là:
\(22\pi + \displaystyle {{33\pi } \over 2} + 24= \left( {38{1 \over 2}\pi + 24} \right)\) \((c{m^2})\).
soanvan.me
