Đề bài
Cho hình vuông \(ABCD\) có \(AB =\) \(3\) cm
Trên tia đối của tia \(BA\) lấy điểm \(K\) sao cho \(BK =\) \(1\) cm
Trên tia đối của tia \(CB\) lấy điểm \(L\) sao cho \(CL =\) \(1\) cm
Trên tia đối của tia \(DC\) lấy điểm \(M\) sao cho \(MD =\) \(1\) cm
Trên tia đối của tia \(AD\) lấy điểm N sao cho \(NA =\) \(1\) cm
Chứng minh KLMN là hình vuông
Phương pháp giải - Xem chi tiết
Chứng minh bốn tam giác vuông \(MCL, LKB, KAN, NDM\) bằng nhau.
Khi đó suy ra: \(ML = LK = KN = NM\) và \( LK\) vuông góc với \(KN\)
Từ đó ta có \(KLMN\) là hình vuông.
Lời giải chi tiết
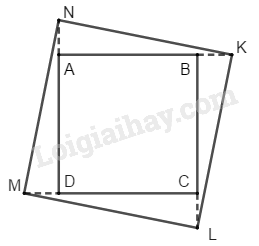
Từ đề bài suy ra \(BK=CL\)\(=MD=NA=1cm\)
Xét \(∆ ANK\) và \(∆ BKL:\)
\(AN = BK\) (gt)
\(\widehat A = \widehat B = 90^\circ \)
\(AK = BL\) (vì \(AB = BC,\, BK = CL\))
Do đó \(∆ ANK = ∆ BKL \,(c.g.c)\)
\(⇒ NK = KL \,(1)\)
Xét \(∆ BKL\) và \(∆ CLM:\)
\(BK = CL\) (gt)
\(\widehat B = \widehat C = 90^\circ \)
\(BL = CM\) (vì \(BC = CD, \,CL = DM\))
Do đó: \(∆ BKL = ∆ CLM (c.g.c)\)
\(⇒ KL = LM \,(2)\)
Xét \(∆ CLM\) và \(∆ DMN :\)
\(CL = DM\) (gt)
\(\widehat C = \widehat D = 90^\circ \)
\(CM = DN\) (vì \(CD = DA,\, DM = AN\))
Do đó: \(∆ CLM = ∆ DMN (c.g.c)\)
\(⇒ LM = MN \,(3)\)
Từ \((1), (2)\) và \((3)\) \(⇒ NK = KL = LM = MN\)
Tứ giác \(MNKL\) là hình thoi
\(∆ ANK = ∆ BKL\) \( \Rightarrow \widehat {ANK} = \widehat {BKL}\)
Trong tam giác \(ANK\) có \(\widehat A = 90^\circ \Rightarrow \widehat {ANK} + \widehat {AKN} = 90^\circ \)
\( \Rightarrow \widehat {BKL} + \widehat {AKN} = 90^\circ \)hay \(\widehat {NKL} = 90^\circ \)
Vậy tứ giác \(MNKL\) là hình vuông.
soanvan.me
