Đề bài
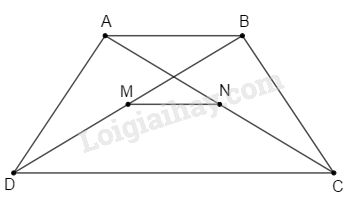
Cho hình thang \(ABCD\) \((AB // CD, AB < CD)\). Gọi trung điểm của các đường chéo \(AC, BD\) thứ tự là \(N\) và \(M. \) Chứng minh rằng:
a) \( MN// AB;\)
b) \(\displaystyle MN = {{CD - AB} \over 2}\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Định lí đảo của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
- Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Tiên đề Ơ-clít: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
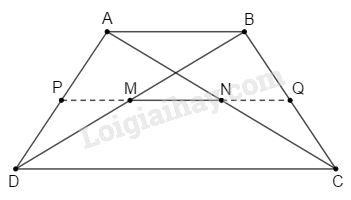
a) Gọi \(P\) là trung điểm của \(AD\), nối \(PM.\)
Xét \(\Delta DAB\) có:
\(\displaystyle{{PA} \over {AD}} = {1 \over 2};{{BM} \over {BD}} = {1 \over 2}\)
\(\displaystyle\Rightarrow {{PA} \over {AD}} = {{BM} \over {BD}}\)
Theo định lí đảo của định lí Ta-lét ta có \( PM // AB\) (1)
Xét \(\Delta ACD\) có: \(\displaystyle{{AP} \over {AD}} = {1 \over 2};{{AN} \over {AC}} = {1 \over 2}\)
\(\Rightarrow \displaystyle{{AP} \over {AD}} = {{AN} \over {AC}}\)
Theo định lí đảo của định lí Ta-lét ta có \(PN // CD\) (2)
\(AB//CD\) (gt) (3)
Từ (1), (2) và (3) suy ra \(PM//AB\) và \(PN//AB\)
Qua \(P\) có hai đường thẳng \(PN\), \(PM\) cùng song song với \(AB\), theo tiên đề Ơ-clít thì \(PN \equiv PM\) hay \( P, M, N\) thẳng hàng.
Vậy \( MN // AB\).
b) Vì \(PM\) là đường trung bình của tam giác \(DAB\) nên ta có:
\(\displaystyle PM = {{AB} \over 2}\) (tính chất đường trung bình tam giác)
Vì \(PN\) là đường trung bình của tam giác \(ADC\) nên ta có:
\(\displaystyle PN = {{CD} \over 2}\) (tính chất đường trung bình tam giác)
Vậy \(MN = PN - PM\) \(\displaystyle= {{CD} \over 2} - {{AB} \over 2} = {{CD - AB} \over 2}\)
soanvan.me
