Đề bài
Cho tam giác \(ABC\). Tìm một điểm \(M\) trên cạnh \(AB\) và một điểm \(N\) trên cạnh \(AC\) sao cho \(MN\) song song với \(BC\) và \(AM = CN\).
Phương pháp giải - Xem chi tiết
- Giả sử dựng được hai điểm \(M,N\) thỏa mãn bài toán.
- Sử dụng các tính chất hình học đã biết để suy ra cách dựng.
Lời giải chi tiết
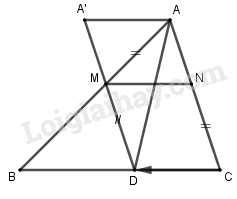
Giả sử đã dựng được hai điểm \(M,N\) thỏa mãn điều kiện đầu bài.
Qua \(M\) kẻ đường thẳng song song với \(AC\) cắt \(BC\) tại \(D\).
Khi đó tứ giác \(MNCD\) là hình bình hành \( \Rightarrow CN = DM\).
Mà \(CN = AM\) (giả thiết) \( \Rightarrow AM = DM\) hay \(\Delta ADM\) cân tại \(M\).
Do đó \(\widehat {MAD} = \widehat {MDA}\), mà \(\widehat {MDA} = \widehat {DAC}\) (so le trong) nên \(\widehat {MAD} = \widehat {DAC}\).
Suy ra \(AD\) là phân giác trong của góc \(A\) nên ta dựng được \(AD\) .
Ta lại có \(\overrightarrow {NM} = \overrightarrow {CD} \) nên \(M = {T_{\overrightarrow {CD} }}\left( N \right)\)
Từ đó suy ra cách dựng:
- Dựng đường phân giác trong của góc \(A\). Đường này cắt \(BC\) tại \(D\).
- Dựng đường thẳng \(d\) là ảnh của đường thẳng \(AC\) qua phép tịnh tiến theo vectơ \(\overrightarrow {CD} \). \(d\) cắt \(AB\) tại \(M\).
- Dựng \(N\) sao cho \(\overrightarrow {NM} = \overrightarrow {C{\rm{D}}} \).
Khi đó dễ thấy \(M,N\) thỏa mãn điều kiện đầu bài.
soanvan.me
