Đề bài
Qua tâm \(G\) của tam giác đều \(ABC\), kẻ đường thẳng \(a\) cắt \(BC\) tại \(M\) và cắt \(AB\) tại \(N\), kẻ đường thẳng \(b\) cắt \(AC\) tại \(P\) và \(AB\) tại \(Q\), đồng thời góc giữa \(a\) và \(b\) bằng \(60^\circ \). Chứng minh rằng tứ giác \(MPNQ\) là một hình thang cân.
Phương pháp giải - Xem chi tiết
Xét phép quay tâm \(G\) góc quay \({120^0}\) và nhận xét.
Lời giải chi tiết
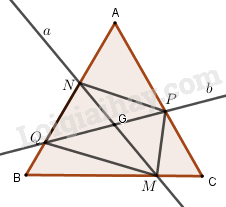
Gọi \({Q_{\left( {G;{{120}^0}} \right)}}\) là phép quay tâm \(G\) góc \({120^0}\).
Phép quay này biến \(b\) thành \(a\), biến \(CA\) thành \(AB\).
Mà \(P = b \cap CA,N = a \cap AB\) nên \({Q_{\left( {G,{{120}^0}} \right)}}\left( P \right) = N\).
Tương tự \({Q_{\left( {G;{{120}^0}} \right)}}\left( Q \right) = M\) suy ra \(GP = GN,GQ = GM\).
\( \Rightarrow \Delta GNQ = \Delta GPM \Rightarrow NQ = PM\)
Vì \({Q_{\left( {G;{{120}^0}} \right)}}\) biến \(PQ\) thành \(NM\) nên \(PQ = NM\).
Từ đó suy ra hai tam giác \(NQM\)và \(PMQ\) bằng nhau. Do đó \(\widehat {NQM} = \widehat {PMQ}\).
Tương tự \(\widehat {QNP} = \widehat {MPN}\).
Từ đó suy ra \(\widehat {PNQ} + \widehat {NQM} = {180^0}\)
Do đó \(NP\parallel QM\). Vậy ta có tứ giác \(MPNQ\) là hình thang cân.
soanvan.me
