Đề bài
Tính các góc \(B\) và \(D\) của hình thang \(ABCD,\) biết rằng \(\widehat A = {60^0},\widehat C = {130^0}.\)
Phương pháp giải - Xem chi tiết
+) Hai góc kề một cạnh bên của hình thang bằng \(180^0.\)
Lời giải chi tiết
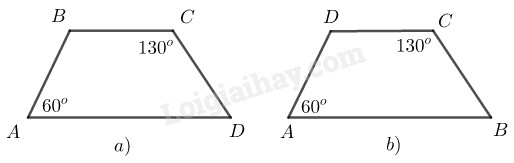
Hình thang \(ABCD\) ta có, \(\widehat A\) và \(\widehat C\) là hai góc đối
\(a)\) Trường hợp \(\widehat A\) và \(\widehat B\) là hai góc kề với cạnh bên.
\(⇒ AD // BC\)
\(\widehat A + \widehat B = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat B = {180^0} - \widehat A = {180^0} - {60^0} = {120^0}\)
\(\widehat C + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat D = {180^0} - \widehat C = {180^0} - {130^0} = {50^0}\)
\(b)\) Trường hợp \(\widehat A\) và \(\widehat D\) là hai góc kề với hai cạnh bên
\(⇒ AB // CD\)
\(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat D = {180^0} - \widehat A = {180^0} - {60^0} = {120^0}\)
\(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat B = {180^0} - \widehat C = {180^0} - {130^0} = {50^0}\)
soanvan.me
