Đề bài
Hình thang \(ABCD\) \((AB // CD)\) có \(\widehat A - \widehat D = {40^0},\widehat A = 2\widehat C\). Tính các góc của hình thang.
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức: Hai góc kề một cạnh bên của hình thang bằng \(180^0.\)
Lời giải chi tiết
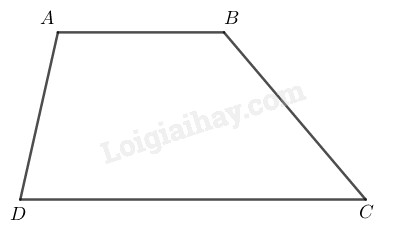
Hình thang \(ABCD\) có \(AB // CD\)
\( \Rightarrow \widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau)
\(\eqalign{
& \widehat A - \widehat D = {40^0}(gt) \cr & \Rightarrow \widehat A + \widehat D+\widehat A - \widehat D = 180^0+{40^0}= {220^0} \cr
& \Rightarrow 2\widehat A = {220^0} \Rightarrow \widehat A = {110^0} \cr
& \widehat D = \widehat A - {40^0} = {110^0} - {40^0} = {70^0} \cr
& \widehat A = 2\widehat C(gt) \cr
& \Rightarrow \widehat C = {{\widehat A} \over 2} = {110^0}:2 = {55^0} \cr} \)
Vì \(AB // CD\) nên \(\widehat B + \widehat C = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat B = {180^0} - \widehat C = {180^0} - {55^0} = {125^0}\)
soanvan.me
